Giải toán 9 Bài 4. Góc tạo bởi tia tiếp tuyến và dây cung

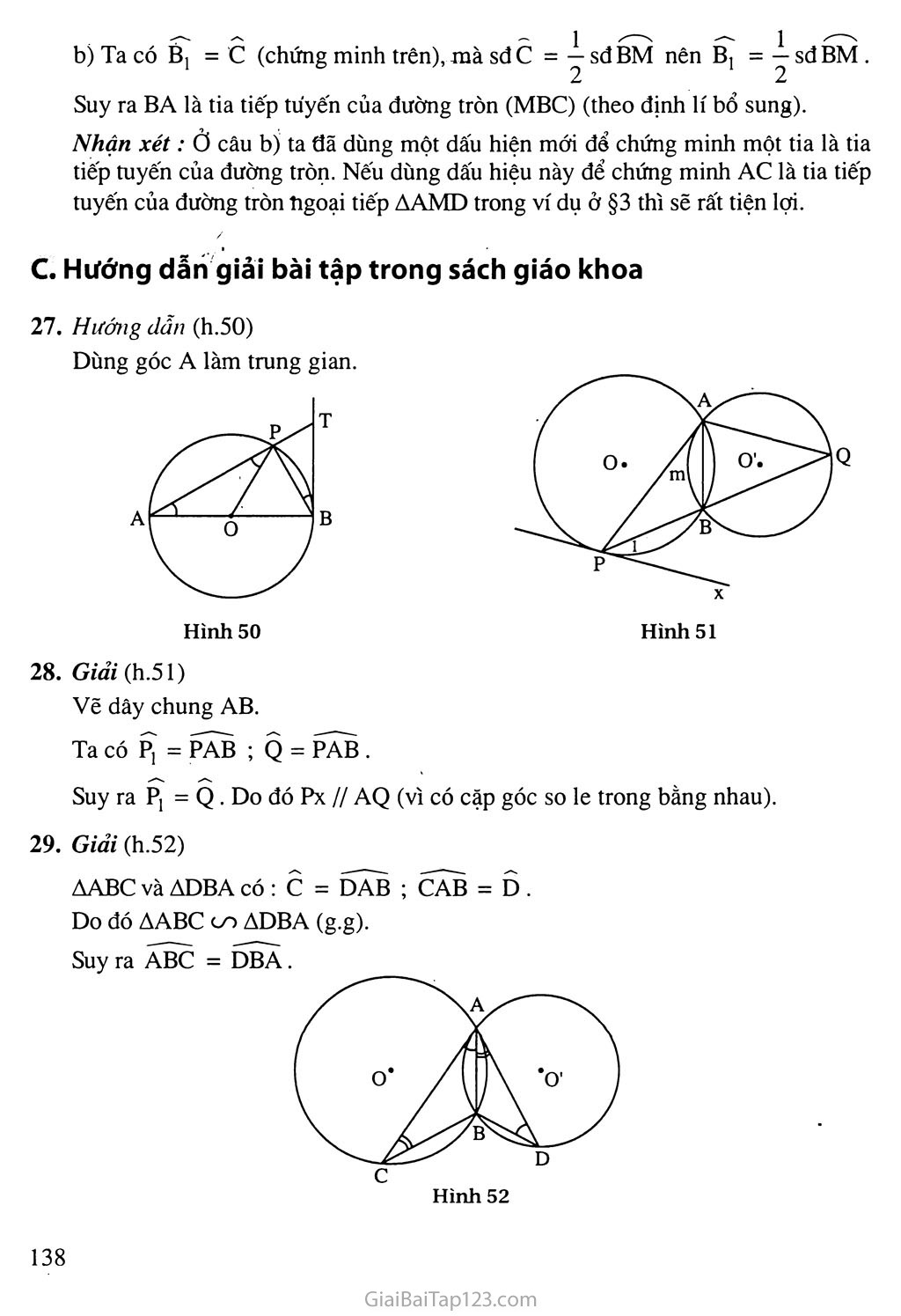
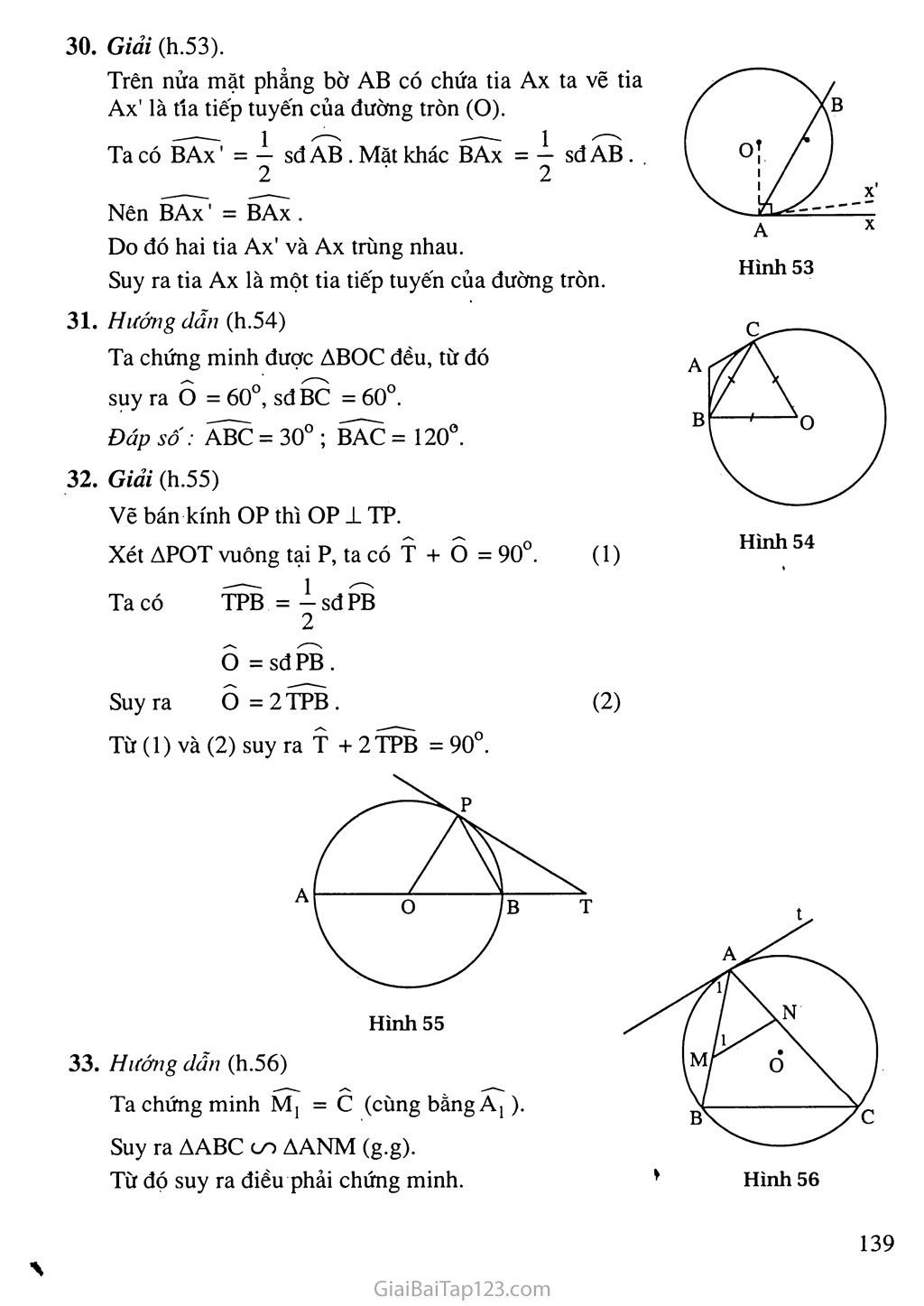
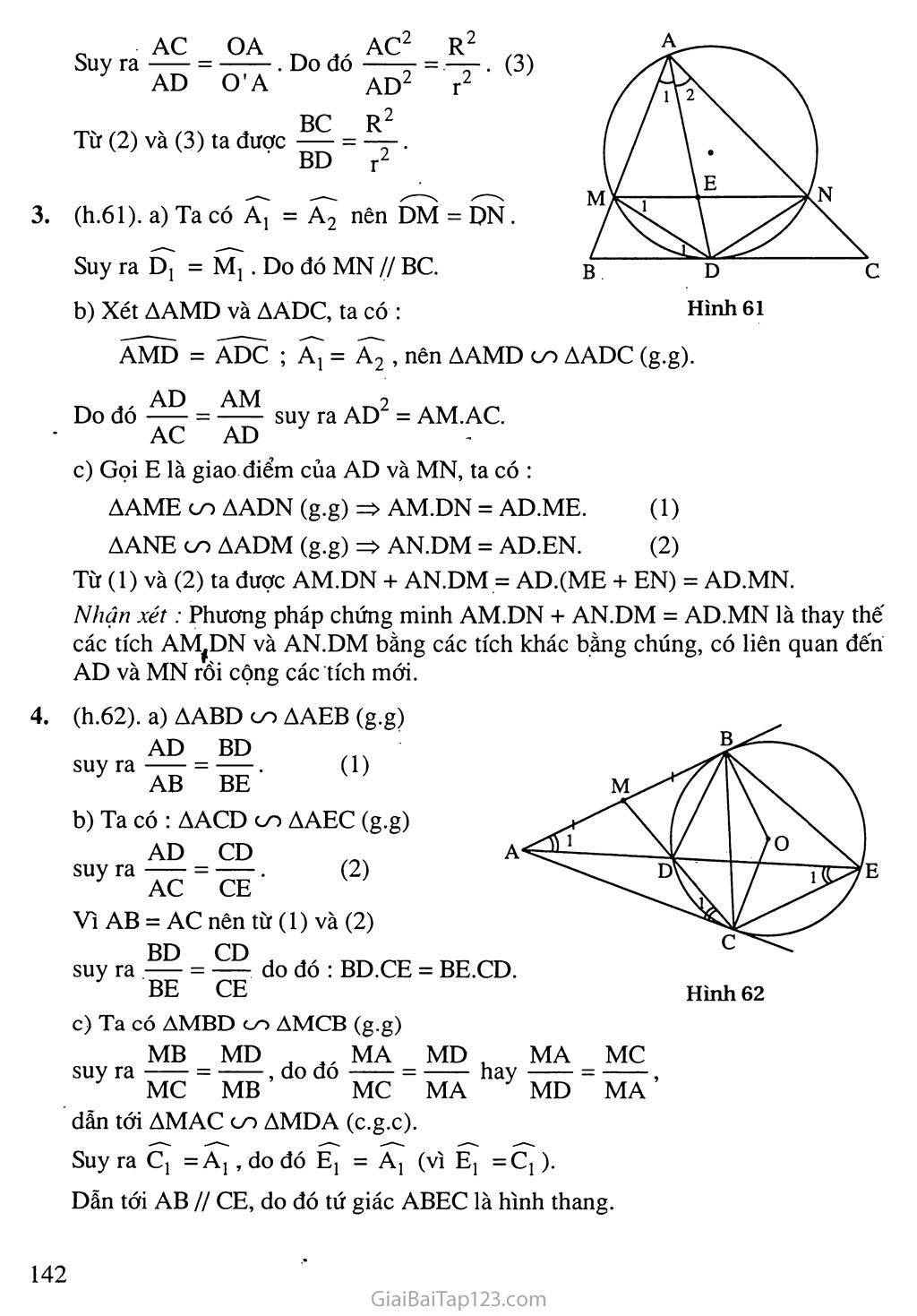
Hình 48
§4. GÓC TẠO BỞI TIA TIẾP TUYÊN VÀ DÂY CUNG
A. Tóm tắt kiến thức
Định lí
Số đo của góc tạo bởi tia tiếp tuyến và dây cung bằng nửa sô'đo của cung bị chắn (lì.48).
BAx = í- sđ AB.
2
Hệ quả
Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.
Định lí (bổ sung)
Nếu góc BAx (cố đỉnh A nằm trên đường tròn, một cạnh chứa dây cung AB) có số đo bằng một nửa số đo của cung AB căng dây đó và cung này nằm bên trong góc đó thì cạnh Ax là một tia tiếp tuyến của dường tròn.
B. Ví dụ
Cho tam giác ABC nội tiếp đường tròn (O). Từ A vẽ tiếp tuyến xy với đường tròn. Qua B vẽ một đường thẳng song song với xy cắt AC tại M. Chứng minh rằng :
AB2 = AM.AC.
BA là tiếp tuyến của đường tròn ngoại tiếp tam giác MBC.
Giải (h.49)
Ta có c - A ị (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung AB). Mặt khác Bj - Aj (so le trong của BM // xy) nên c =Bj .
Đo đó AABM co ÀACB (g.g).
AB AM . ^2	... .
Suy ra —— = —7 => AB = AM.AC.
AC AB
Ta có Bj = c (chứng minh trên), mà sđ c =
— sđBM nên B, 2
ịsđBM.
2
Suy ra BA là tia tiếp túyến của đường tròn (MBC) (theo định lí bổ sung).
Nhận xét: Ở câu b) ta đã dùng một dấu hiện mới để chứng minh một tia là tia tiếp tuyến của đường tròn. Nếu dùng dấu hiệu này để chứng minh AC là tia tiếp tuyến của đường tròn tigoại tiếp AAMD trong ví dụ ở §3 thì sẽ rất tiện lợi.
/ ..
c. Hướng dẫn giải bài tập trong sách giáo khoa
27. Hướng dẫn (h.50)
Dùng góc A làm trung gian.
Hình 50
Giải (h.51)
Vẽ dây chung AB.
Ta có Pj = PAB ; Q = PAB .
Suy ra P! = Q . Do đó Px // AQ (vì có cặp góc so le trong bằng nhau).
Giải (h.52)
AABC và ADBA có: c = DAB ; CAB = D .
Do đó AABC co ADBA (g.g).
Giải (h.53).
Hình 53
Trên nửa mặt phảng bờ AB có chứa tia Ax ta vẽ tia Ax' là tía tiếp tuyến của đường tròn (O).
Ta có BAx' = 4 sđ AB . Mặt khác BAx = 4 sđ AB . . 2 2
Nên BAx' = BAx.
Do đó hai tia Ax' và Ax trùng nhau.
Suy ra tia Ax là một tia tiếp tuyến của đường tròn.
Hướng dẫn (h.54)
Ta chứng minh được ABOC đều, từ đó suy ra ô = 60°, sdBC =60°.
Đáp số: ABC = 30° ; BAC = 120°.
Giải (h.55)
Vẽ bán kính OP thì OP ± TP.
Xét APOT vuông tại p, ta có T + o = 90°.	(1)
Ta có TPB = 4 sđ PB 2
ô = sdPB.
Suy ra 0=2 TPB.	(2)
Từ (1) và (2) suy ra T + 2TPB = 90°.
33. Hướng dẫn (h.56)
Hình 57
34. Giải (h.57)
Nối TA, TB. Ta được Tj = B.
AMTA co AMBT (g.g). Suy ra	.
MB MT
Do đó MT2 = MA.MB.
Nhận xét : Bài toán này là một định lí hay dùng. Bạn nên nhớ để vận dụng.
35. Giải (h.58)
Gọi M là đỉnh ngọn hải đăng và M' là điểm quan sát trên tàu. Đường thẳng MM' tiếp xúc với mặt biển
tại T.
Vẽ cát tuyến MAB đi qua o.
Ta có
MT2 = MA.MB = MA.(MA + 2R). MT2 = 0,04.(0,04 + 2.6400)
MT « 23 (km).
Tương tự ta có M'T » 1 lkm.
Đáp số: 34km.
D. Bài tập luyện thêm
Cho nửa đường tròn đường kính AB. Từ một điểm M trên nửa đường tròn, vẽ tiếp tuyến xy với nửa đường tròn và vẽ MH ± AB. Vẽ đường tròn (M ; MH) cắt xy tại c và D (C và A thuộc cùng một nửa mặt phẳng bờ HM). Chứng minh rằng :
MA, MB là các tia phân giác của các góc tạo bởi xy và MH.
AC và BD là các tiếp tuyến của đường tròn (M).
Cho đường tròn (O ; R) và đường tròn (O' ; r) cắt nhau tại A và B. Vẽ dây AC của đường tròn (O) tiếp xúc với đường tròn (O'). Vệ dây AD của đường tròn (O') tiếp xúc với đường tròn (O). Chứng minh rằng :
a) BC.BD = AB2 ;
Cho tam giác ABC, đường phân giác AD ; Một đường tròn đi qua A và tiếp xúc với BC tại D cắt AB và AC lần lượt tại M và N. Chứng minh rằng :
MN//BC;
AD2 = AM.AC ;
AMỵĐN + AN.DM = AD.MN.
Từ một điểm A, ở ngoài đường tròn (O) vẽ các tiếp tuyến AB, AC với đường tròn (B, c là các tiếp điểm). Gọi M là trung điểm của AB và gọi D là giao điểm của MC với đường tròn. Đường thẳng AD cắt đường tròn tại một điểm thứ hai là E. Chứng minh rằng :
AD BD a AB - BE’
Tứ giác BDCE có tích các cặp cạnh đối bằng nhau ;
>
1.
Tứ giác ABEC là hình thang.
Hướng dẫn - Đáp sô'
(h.59).	
Hình 59
Mj = Bj ; M2 = B| (cùng phụ với MAH ). Suy ra Mj = M2 •
Chứng minh tương tự được M3 = M4 .
Ta có AAMC = AAMH (c.g.c).
Suy ra c = H = 90°. Do đó AC là tiếp tuyến của đường tròn (M). Chứng minh tương tự, BD là tiếp tuyến của đường tròn (M).
2.
(h.60). a) AABC GO ADBA (g.g). AB _ BC _ AC BD - BA - AD '
Suy ra
(1)
Do đó AB = BC.BD.
,, ™	Á6 12 - AC AC
b) Từ (1) ta có 7—.—— = ——.
BD BA AD AD
Do đó
BC
BD
ACj
AD2
Mặt khác, ta có OAD = O'AC = 90°, suy ra OAC = O'AD. Vậy AAOC GO AAƠD (g.g).
e„.._„AC OA ^,XAC2 Suy ra ——- =	. Do đó ——
AD O'A	ad2
Từ (2) và (3) ta được	.
^,3)
Hình 61
BD I"
(h.61). a) Ta có A) = A2 nênDM = DN.
Suy ra Dị = Mj . Do đó MN // BC.
Xét AAMD và AADC, ta có :
AMD = ADC ; Aj = A2 , nên AAMD co AADC (g.g).
Do đó	suy ra AD2 = AM.AC.
AC AD
Gọi E là giao điểm của AD và MN, ta có :
AAME co AADN (g.g) => AM.DN = AD.ME.	(1)
AANE co AADM (g.g) => AN.DM = AD.EN.	(2)
Từ (1) và (2) ta được AM.DN + AN.DM = AD.(ME + EN) = AD.MN.
Nhận xét: Phương pháp chứng minh AM.DN + AN.DM = AD.MN là thay thế các tích AMfDN và AN.DM bằng các tích khác bằng chúng, có liên quan đến AD và MN rồi cộng các'tích mới.
(h.62). a) AABD co AAEB (g.g)
AD _ BP
suy ra —— = ——.	(1)
AB BE
b) Ta có : AACD co AAEC (g.g)
suy ra
(2)
Hình 62
AD
CD
AC CE '
Vì AB = AC nên từ (1) và (2)
BD CD , '	''
suy ra	do đó : BD.CE = BE.CD.
BE CE
c) Ta có AMBD co AMCB (g.g)
MB
MD , MA MC hay —- = — MD MA
MD J MA
, do đó
suy ra
MC MB	MC MA
dẫn tới AMAC co AMDA (c.g.c).
Suy ra Cj =Aj, do đó Eị = Aj (vì Ej =Cj).
Dẫn tới AB // CE, do đó tứ giác ABEC là hình thang.