Giải toán 9 Bài 5. Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn
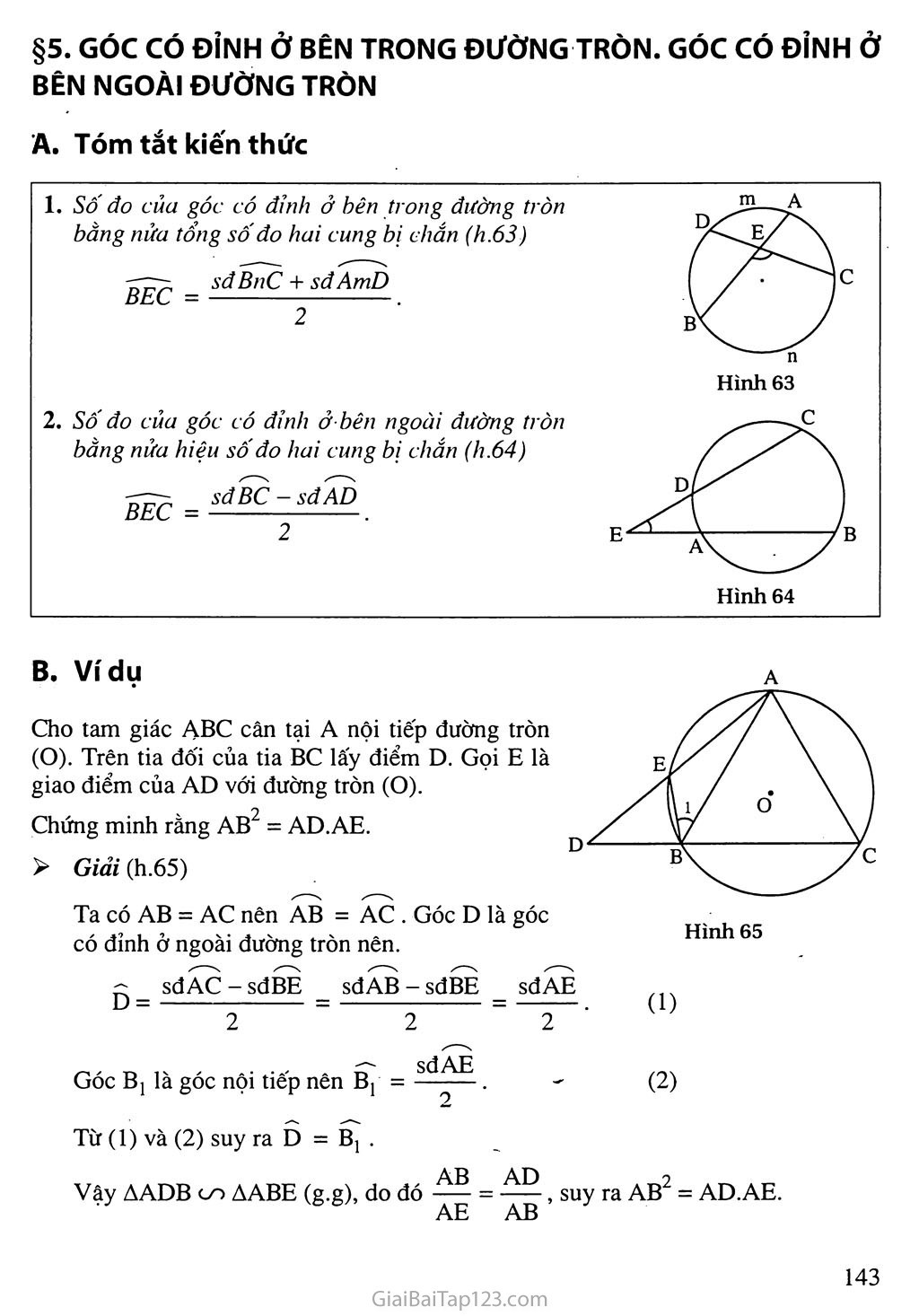
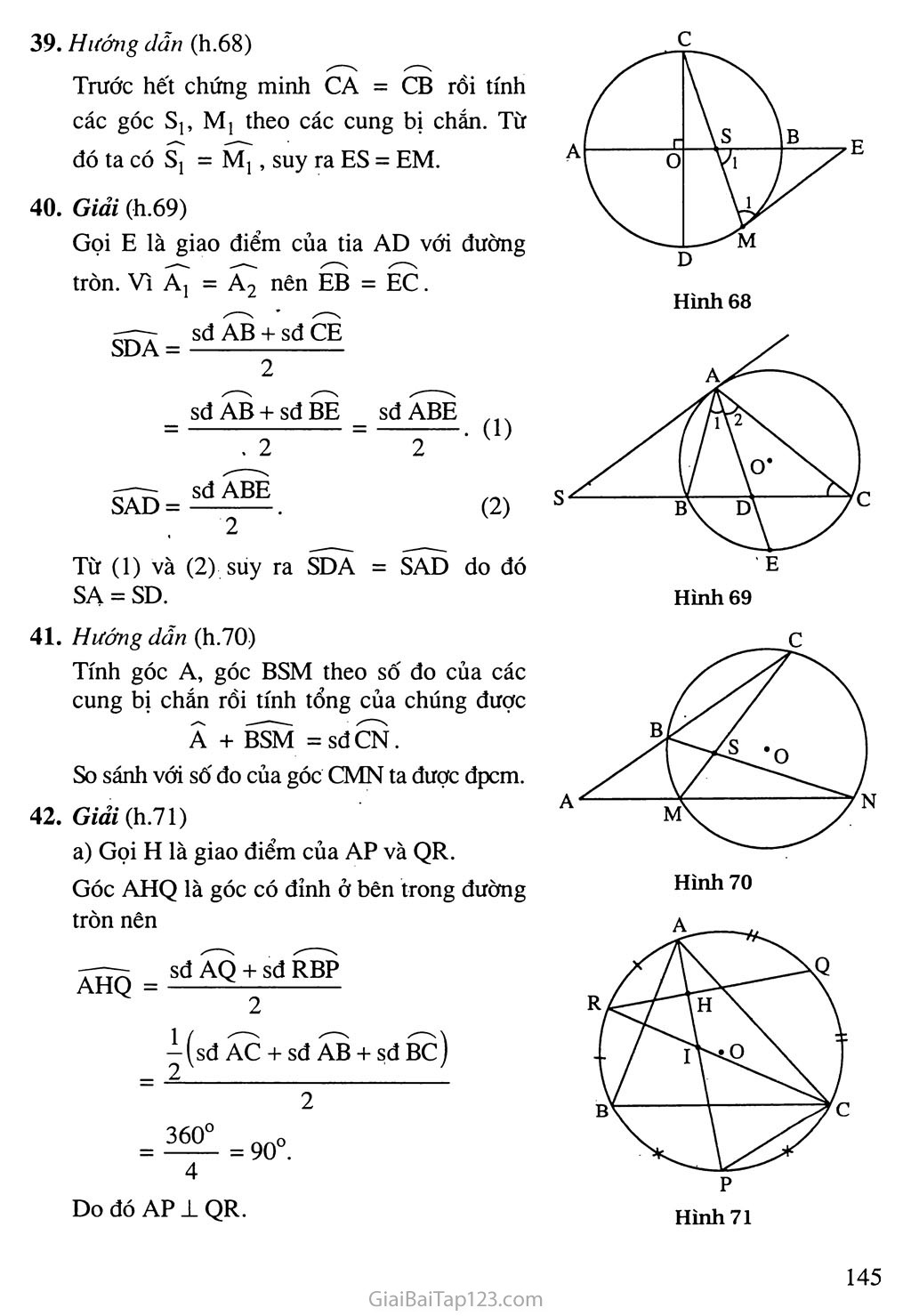
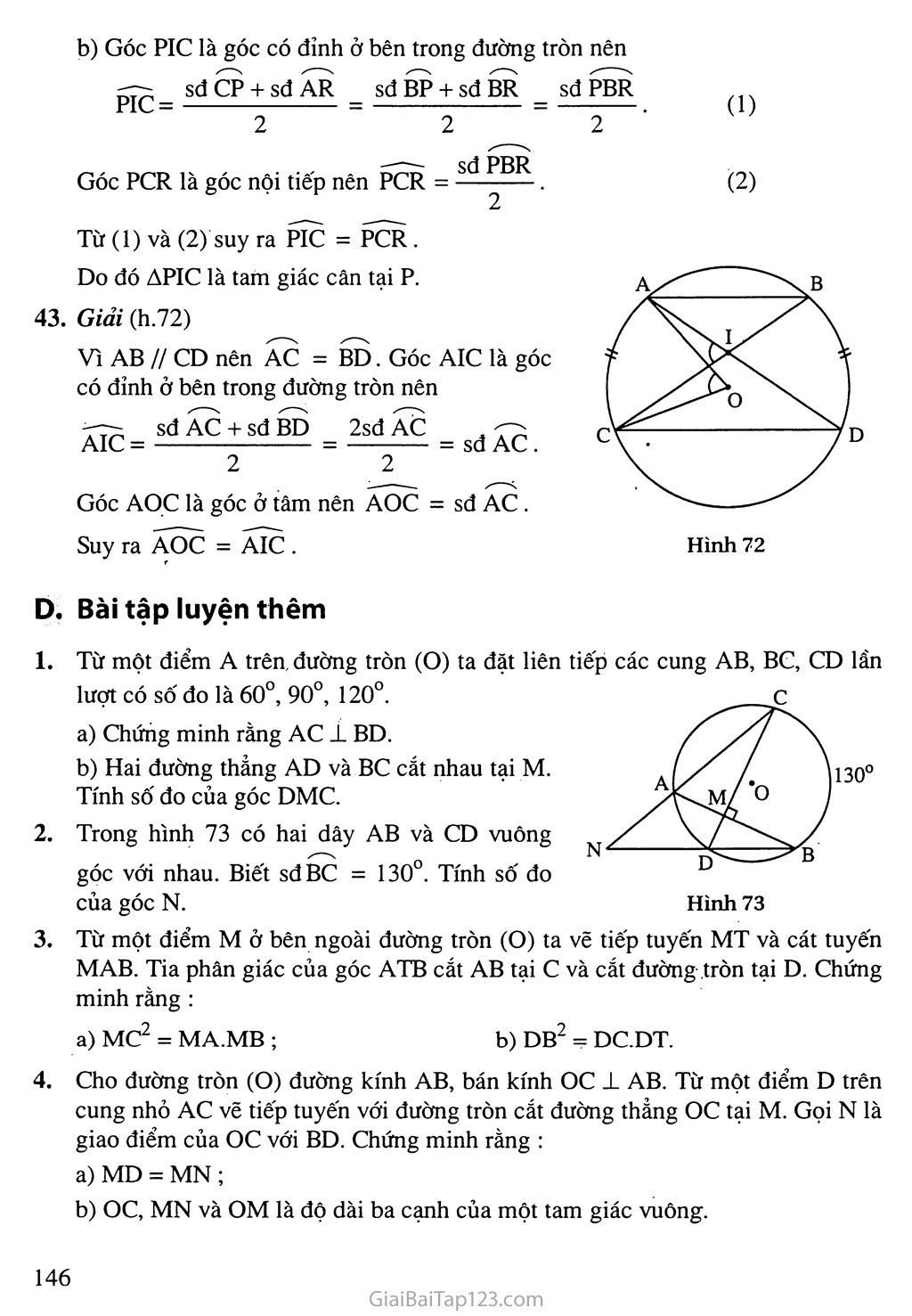
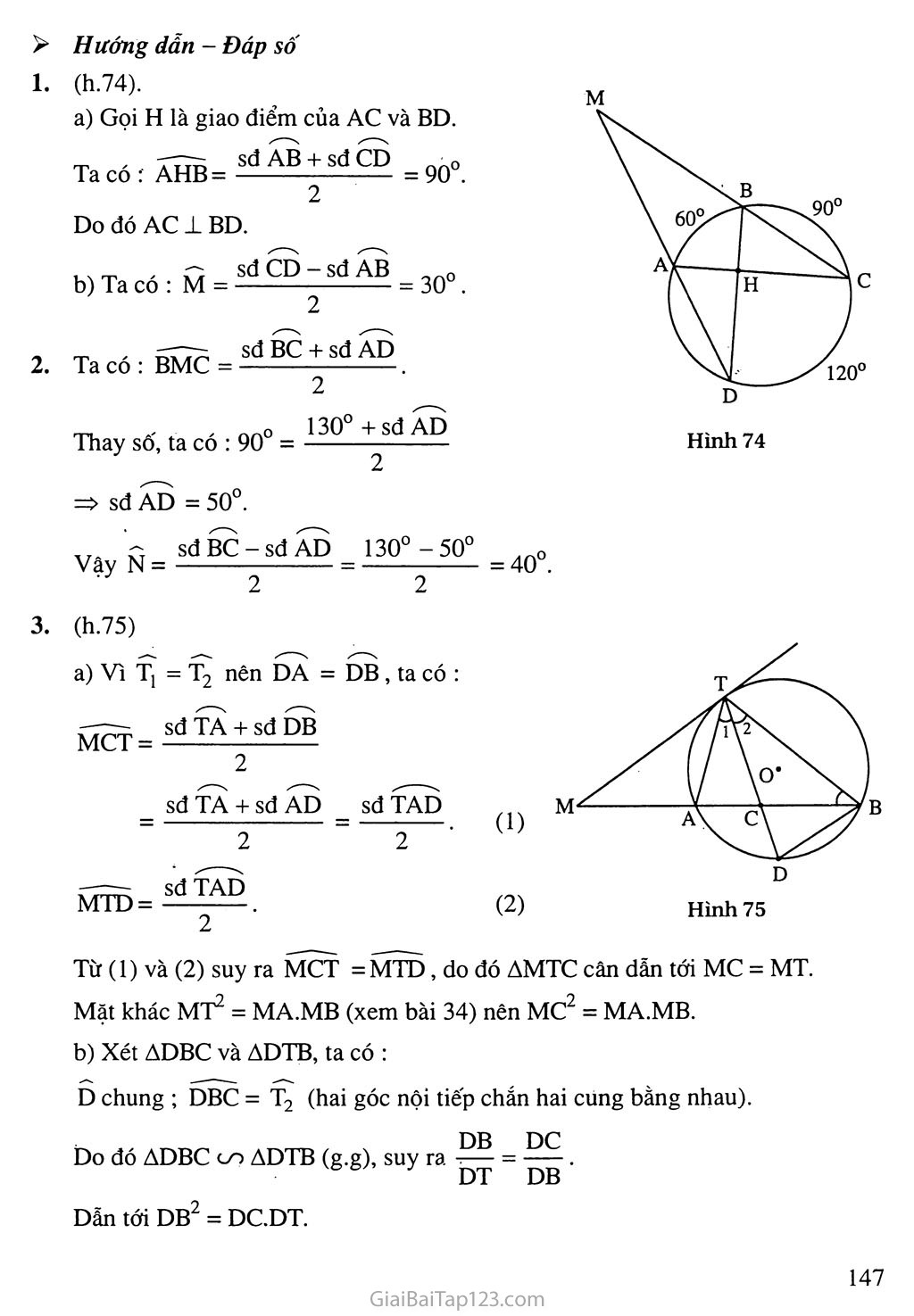
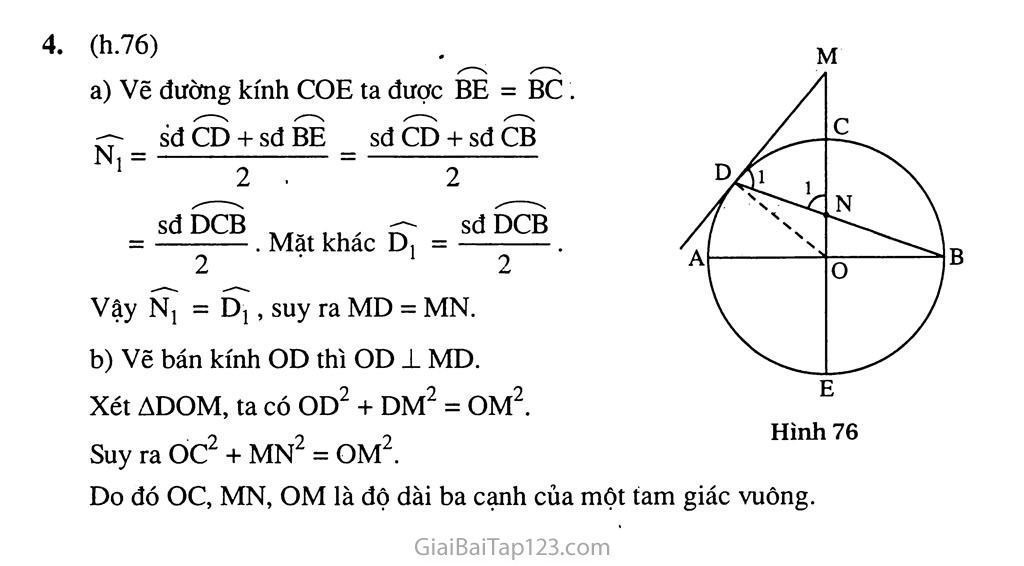
§5. GÓC CÓ ĐỈNH Ở BÊN TRONG ĐƯỜNG TRÒN. GÓC CÓ ĐỈNH Ở BÊN NGOÀI ĐƯỜNG TRÒN A. Tóm tắt kiến thức 1. Số đo của góc có đỉnh ở hên trong đường tròn bằng nửa tổng số đo hai cung bị chắn (h.63) BEC = sđBnC + sđAmD 2. Sô' đo của góc có đỉnh ở bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn (h.64) BEC = sđBC - sđAD B. Ví dụ Cho tam giác ẠBC cân tại A nội tiếp đường tròn (O). Trên tia đối của tia BC lấy điểm D. Gọi E là giao điểm của AD với đường tròn (O). Chứng minh rằng AB- , í? sđAE Góc B] là góc nội tiếp nên Bj = . Từ (1) và (2) suy ra D = Bị . AB AD Vậy AADB on AABE (g.g), do đó —— = ——, suy ra AB = AD.AE. AE AB = AD.AE. > Giải (h.65) Ta có AB = AC nên AB = AC . Góc D là góc có đỉnh ở ngoài đường tròn nên. Hình 65 m A Hình 64 (1) (2) ~ _ sđAC - sđBE _ sđAB - sđBE _ sđAE 2 Nhận xét: Trong ví dụ này, khi tính số đo của góc D ta đã thay thế cung AC bởi cung AB bằng nó. Nói chung khi phải tính tổng (hay hiệu) số đo của hai cung ta thường dùng phương pháp thay thế một cung bởi cung khác bằng nó để được hai cung liền nhau (nếu tính tổng) hoặc hai cung có một phần chung (nếu tính hiệu). c. Hướng dẫn giải bài tập trong sách giáo khoa 36. Giải (h.66). Góc AEH và góc AHE là các góc có đỉnh ở bên trong đường tròn nên : AEH = sđ AN + sđ BM (1) AHE = sđ CN + sđ AM (2) Mặt khác AN = CN ; BM= AM nên từ (1) và (2) ta có AEH = AHE . Do đó AAEH là tam giác cân. Hướng dẫn : Giải tương tự như cách giải trong ví dụ của xoắn này. Giải (h.67) a) Góc E và góc T là các góc có đỉnh ở ngoài đường tròn nên : sdAB-sdCD _ 180° -60° 2 - 2 sd CAB - sd CDB 240° - 120° = 60°. = 60°. Do đó E = T. b) Góc TCD là góc giữa tia tiếp tuyến và một dây nên TCD = ịsđCD =30°. 2 Góc BCD là góc nội tiếp nên BCD = — sđBD = 30°. Vậy TCD = BCD, do đó CD là tia phân giác của góc BCT. Hình 67 SDA = sđ AB + sđ BE _ sđ ABE SAD = . 2 sđẤẼE . (1) (2) Hình 68 Hình 69 360° = 90°. Do đó AP 1 QR. Hướìỉg dẫn (h.68) Trước hết chứng minh CA = CB rồi tính các góc Sj, Mj theo các cung bị chắn. Từ đó ta có Sj - Mj, suy ra ES = EM. Giải (h.69) Gọi E là giao điểm của tia AD với đường tròn. Vì Aj = A2 nên EB = EC. sđ AB + sđ CE Từ (1) và (2) suy ra SDA = SAD do đó SẠ = SD. Hướng dẫn (h.70) Tính góc A, góc BSM theo số đo của các cung bị chắn rồi tính tổng của chúng được A + BSM =sdCN. So sánh với số đo của góc CMN ta được đpcm. Giải (h.71) a) Gọi H là giao điểm của AP và QR. Góc AHQ là góc có đỉnh ở bên trong đường tròn nên 7777- sđ AQ + sđ RBP AHQ = —— ị(sđ AC + sđ AB + sđ Ỗc) = 22 _ (1) b) Góc PIC là góc có đỉnh ở bên trong đường tròn nên _ sđ CP + sđ AR _ sđ BP + sđ BR _ sđ PBR Góc PCR là góc nội tiếp nên PCR = sdPBR (2) Tính số đo của góc DMC. Trong hình 73 có hai dây AB và CD vuông góc với nhau. Biết sđBC = 130°. Tính số đo của góc N. Từ một điểm M ở bên ngoài đường tròn (O) ta vẽ tiếp tuyến MT và cát tuyến MAB. Tia phân giác của góc ATB cắt AB tại c và cắt đường.tròn tại D. Chứng minh rằng : a) MC2 = MA.MB ; b) DB2 - DC.DT. Cho đường tròn (O) đường kính AB, bán kính oc ± AB. Từ một điểm D trên cung nhỏ AC vẽ tiếp tuyến với đường tròn cắt đường thẳng oc tại M. Gọi N là giao điểm của oc với BD. Chứng minh rằng : MD = MN ; oc, MN và OM là độ dài ba cạnh của một tam giác vuông. Từ (1) và (2) suy ra PIC = PCR . Do đó APIC là tam giác cân tại p. 43. Giải (h.72) Vì AB // CD nên AC = BD. Góc AIC là góc có đỉnh ở bên trong đường tròn nên 7—~ sđ AC + sđ BD 2sđ AC . -77; 2 2 Góc AỌC là góc ở tâm nên AOC = sđ AC . Suy ra Ấõc = Ấĩc . D. Bài tập luyện thêm Từ một điểm A trên đường tròn (O) ta đặt liên tiếp các cung AB, BC, CD lần lượt có số đo là 60°, 90°, 120°. Chứng minh rằng AC ± BD. Hai đường thẳng AD và BC cắt nhau tại M. 130° > Hướng đẫn - Đáp số 1. (h.74). a) Gọi H là giao điểm của AC và BD. To oA , ALTD- sđ AB + sđ CD o Ta có : AHB= ——-— = 90 . 2 Do đó AC 1 BD. b) Ta có : M = sđ CD - sđ AB = 30°. - Tn oA . ŨÃÃ? _ sđ BC + sđ AD Ta có : BMC = . 2 TKO..OA- „A.nnO_ 130°+sđẤD Thay số, ta có : 90 = — => sđ AD = 50°. , ‘Ct sdBC-sdAD 130°-50° O Vậy N = —— = —— = 40 . 2 2 (h.75) a) Vì Tị = T2 nên DA = DB , ta có : sđ TA + sđ DB MCT = MTD = sđ TA + sđ AD _ sđ TAD "~2 - 2~ sđ TAD (1) (2) Hình 75 Từ (1) và (2) suy ra MCT = MTD , do đó AMTC cân dẫn tới MC = MT. Mặt khác MT2 = MA.MB (xem bài 34) nên MC2 = MA.MB. b) Xét ADBC và ADTB, ta có : D chung ; DBC = T2 (hai góc nội tiếp chắn hai cung bằng nhau). _ . ' DB DC Do đó ADBC co ADTB (g.g), suy ra —— = —— . DT DB Dẫn tới DB2 = DC.DT. B (h.76) Ni = Vẽ đường kính COE ta được BE = BC . sd CD + sđ BE _ sđ CD + sđ CB 2 . " 2 sdDCB — sđ DCB = ———— . Mặt khác D, = . 2 2 Vậy Nj = Dj, suy ra MD = MN. Vẽ bán kính OD thì OD ± MD. Xét ADOM, ta có OD2 + DM2 = OM2. Suy ra oc2 + MN2 = OM2. Do đó oc, MN, OM là độ dài ba cạnh của một tam giác vuông.