Giải bài tập Toán 11 Bài 1. Đại cương về dường thẳng và mặt phẳng

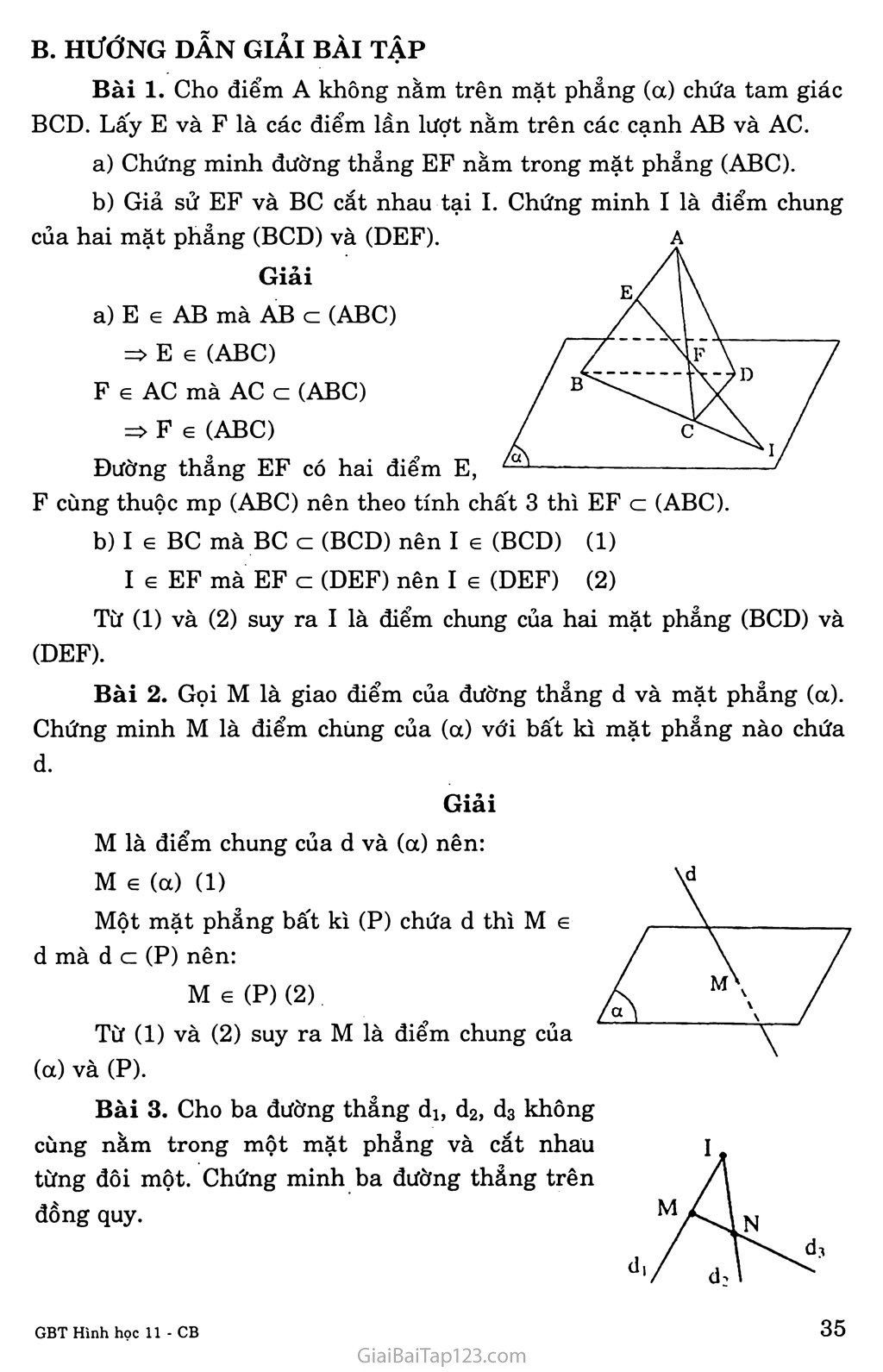
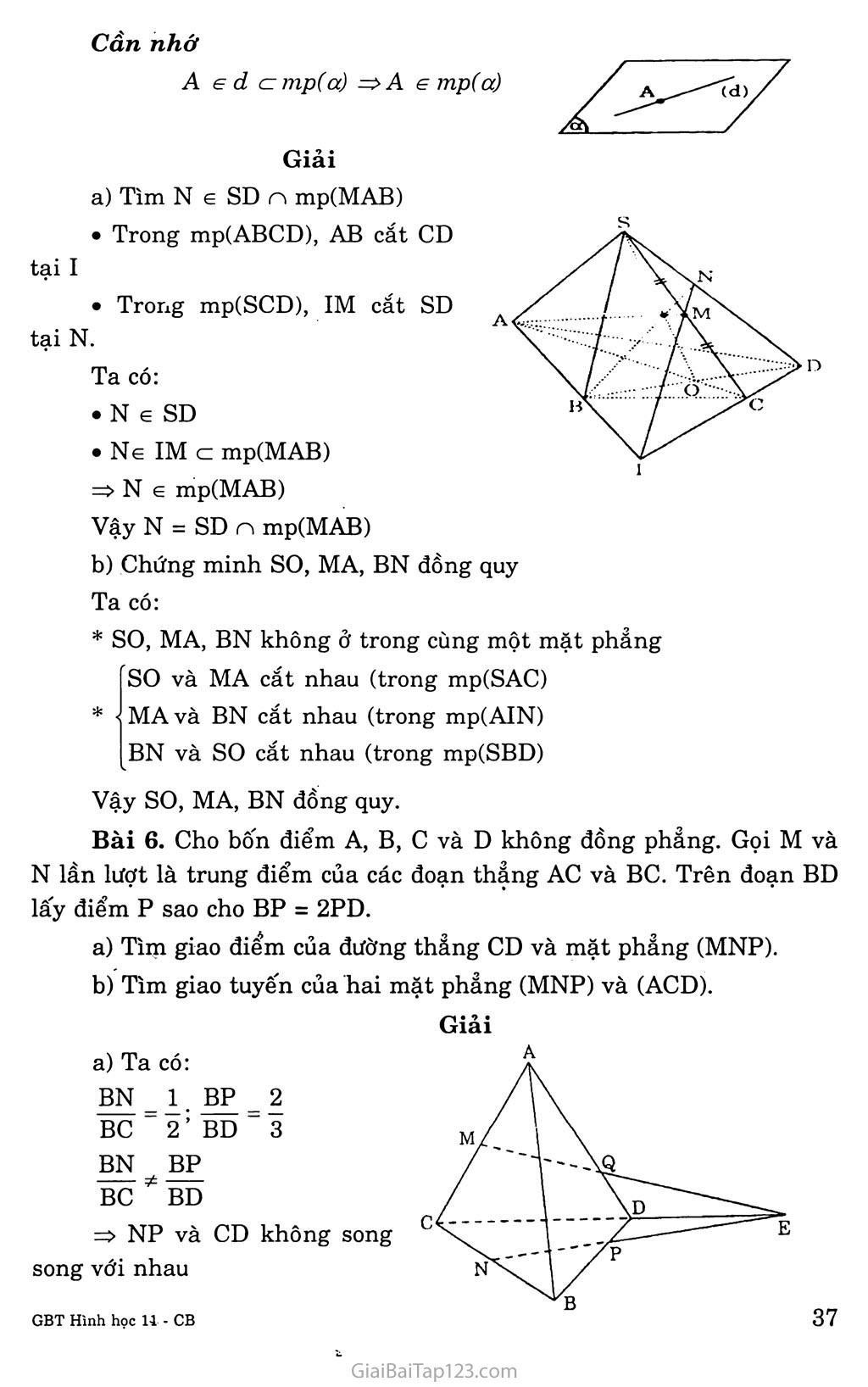
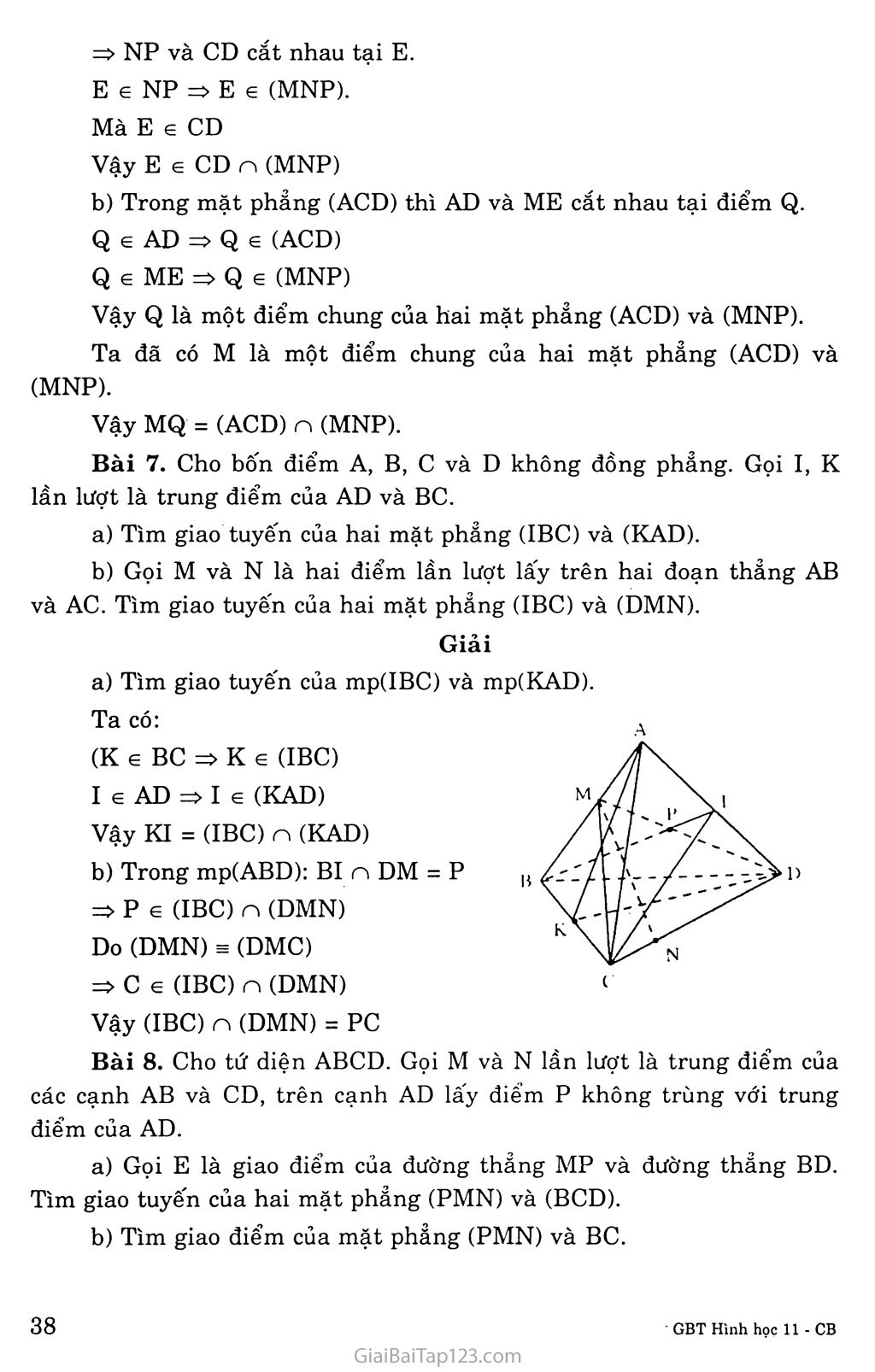
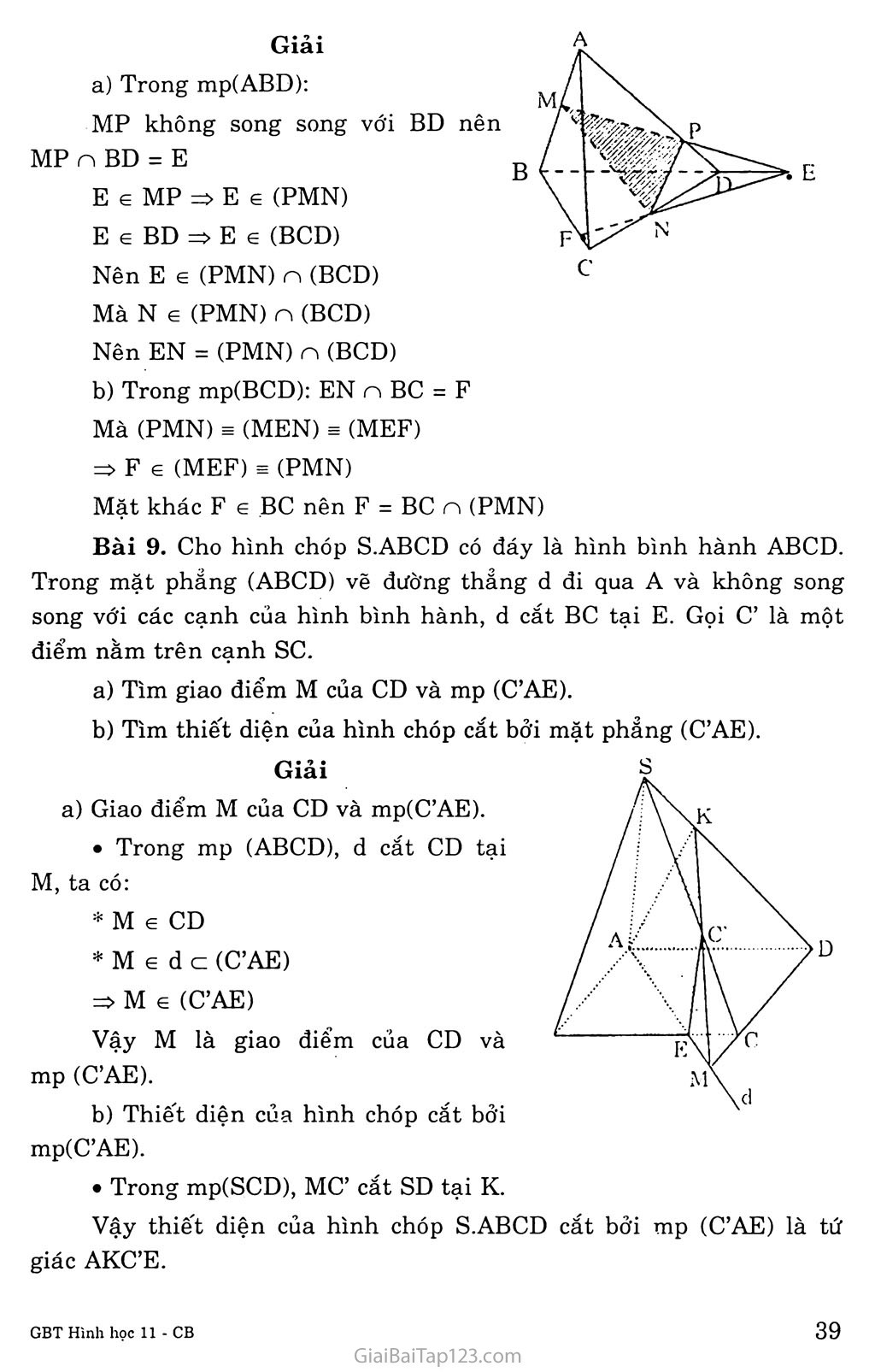
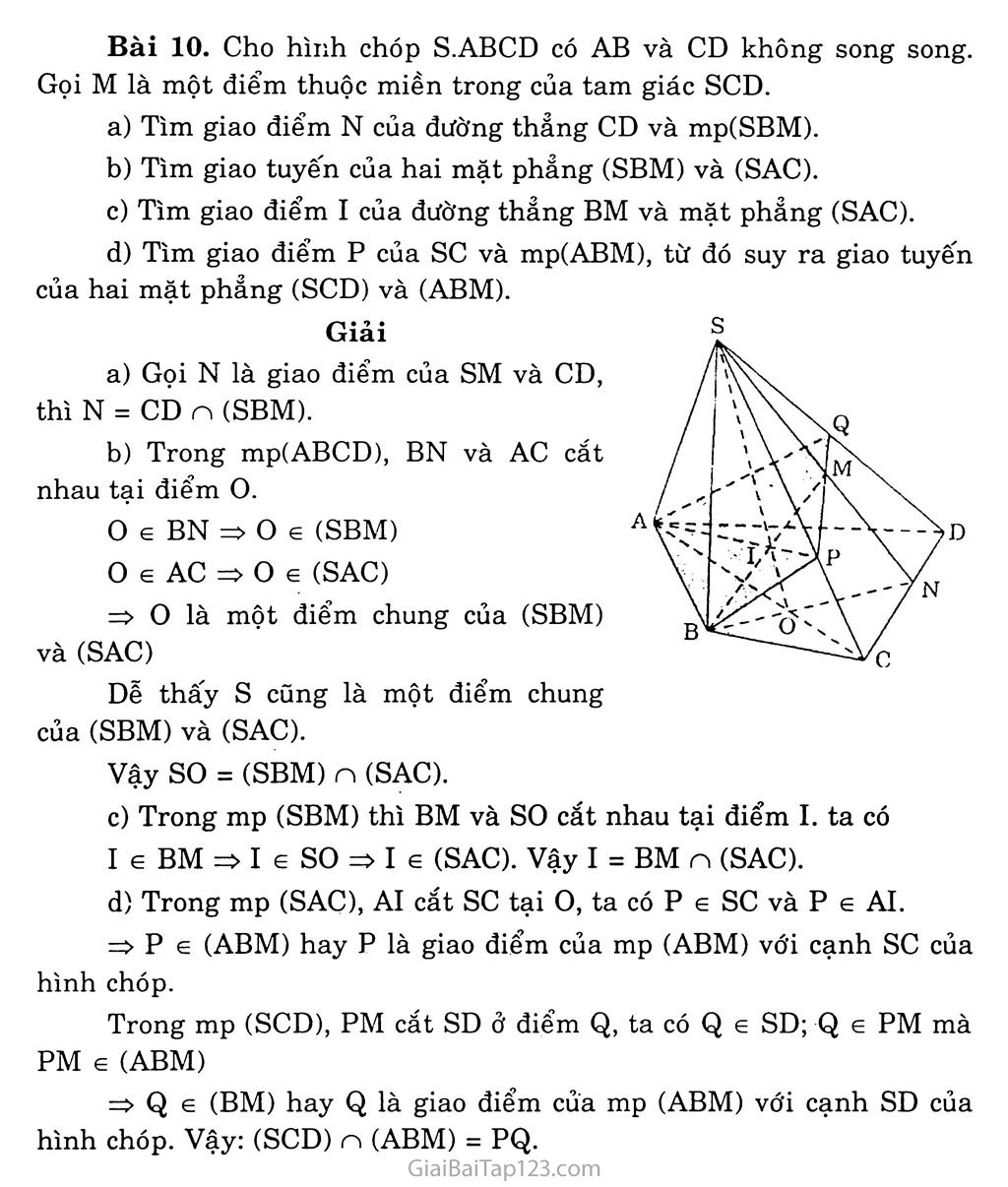
Chương II
ĐƯỜNG THẲNG VÀ MẶT PHANG trong không gian
QUAN HỆ SONG SONG
Bài 1. ĐẠI CƯƠNG VỂ ĐƯỜNG THANG và mặt phang
A. KIẾN THỨC CẦN NAM vững
Khái niệm
Mặt phẳng
Mặt nước hồ yên lặng cho ta hình ảnh một phần của mặt phảng. Mặt phảng không có bề dày và không có giới hạn.
• Để biểu diễn một mặt phẳng ta thường dùng một hình bình hành hay một miền góc và ghi tên của mặt phẳng vào một góc của hình biểu diễn.
• Để kí hiệu một mặt phẳng, ta thường dùng chữ cái hoa như p, Q, R... hay a, p, Ỵ... và có thể đặt chúng trong ngoặc khi cần thiết như (R), (Q), (ã), (p)...
Điểm thuộc mặt phẳng
Khi điểm A thuộc mặt phẳng a ta nói: A nằm trên a hay a chứa A, hay a đi quá A và kí hiệu A 6 CC.
Nếu điểm B không nằm trên a, ta ghi Bia.
Các tính chất thừa nhận
Tính chất thừa nhận lĩ
Có một và chỉ một đường thẳng đi qua hai điểm phân biệt cho trước
Tóm tắt:
• A và B phân biệt
• A qua A và B
■ => A duy nhất
Tính chất thừa nhận 2:
Có một và chỉ một mặt phảng đi qua ba điểm không thẳng hàng cho trước.
=> mp(ABC) duy nhất
m.	• A, B, c phân biệt
Tóm tắt:	’1 \\
• và không thăng hàng
Tính chất thừa nhận 3:
Tồn tại bôn điểm không cùng nằm trên một mặt phẳng
Tính chất thừa nhận 4:
Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất chứa tất cả các điểm chung của hai mặt phẳng đó.
..í. • (P) và (0) phân biệt ì	„
Tóm tắt: À	„2' ' Á 22 ^=> 3 A 3 A Với A cz (P) và A c
. A e (P)vàA G (Q)J
(Q)
(Kí hiệu 3! đọc là tồn tại duy nhất) Chú ý-. A là giao tuyến của (P) và (Q) Kí hiệu: A = (P) n (Q)
Tính chất thùa nhận 5:
Trên một mặt phẳng, các kết quả đã biết trong hình học phẳng đều đúng.
Định lít Nếu một đường thẳng đi qua hai điểm phân biệt của một mặt phảng thì đường thẳng đó nằm trên mặt phảng ấy.
A e (P) và B e (P)ì
Tóm tắt:	2,	f => AB cz (P)
A và B phân biệt
Điều kiện xác định mặt phẳng
Một mặt phẳng được xác định nếu nó đi qua ba điểm không thẳng hàng.
Một mặt phẳng được xác định nếu biết nó đi qua một đường thẳng và một điểm không thuộc đường thẳng đó.
Một mặt phẳng được xác định nếu biết nó đi qua hai đường thẳng cắt nhau.
Hình chóp
Định nghĩa:
Hình chóp là một vật thể hình học giới hạn bởi một đa giác phảng (có thể một tam giác), các mặt còn lại là tam giác có chung đỉnh.
Hình tứ diện được coi là hình chóp theo bốn cách khác nhau.
B. HƯỚNG DẪN GIẢI BÀI TẬP
Bài 1. Cho điểm A không nằm trên mặt phảng (a) chứa tam giác BCD. Lấy E và F là các điểm lần lượt nằm trên các cạnh AB và AC.
a) Chứng minh đường thẳng EF nằm trong mặt phẳng (ABC).
của hai mặt phẳng (BCD) và (DEF).
Giải
b) Giả sử EF và BC cắt nhau tại I. Chứng minh I là điểm chung
a) E e AB mà AB c (ABC)
=> E e (ABC)
F e AC mà AC c (ABC)
=> F e (ABC)
Đường thẳng EF có hai điểm E,
F cùng thuộc mp (ABC) nên theo tính chất 3 thì EF c (ABC).
b) I e BC mà BC c (BCD) nên I e (BCD) (1)
I e EF mà EF c (DEF) nên I 6 (DEF) (2)
Từ (1) và (2) suy ra I là điểm chung của hai mặt phảng (BCD) và (DEF).
Bài 2. Gọi M là giao điểm của đường thẳng d và mặt phảng (a). Chứng minh M là điểm chúng của (a) với bất kì mặt phẳng nào chứa d.
Giải
M là điểm chung của d và (a) nên:
M e (a) (1)
Một mặt phảng bất kì (P) chứa d thì M 6 d mà d C2 (P) nên:
M 6 (P) (2)
Từ (1) và (2) suy ra M là điểm chung của (a) và (P).
Bài 3. Cho ba đường thẳng di, d2, d3 không cùng nằm trong một mặt phẳng và cắt nhau từng đôi một. Chứng minh ba đường thẳng trên đồng quy.
Giải
Gọi I = di n d2
Giả sử d3 không qua I:
Khi đó phải cắt di, d2 lần lượt tại M, N khác I => d3 đồng phảng với di, d2: điều này mâu thuẫn!
Vậy d3 đồng qui với di, d2tại I
Bài 4. Cho bôn điểm A, B, c và D không đồng phẳng. Gọi Ga, Gb, Gc, Gd lần lượt là trọng tâm của các tam giác BCD, CDA, ADB, ACB. Chứng minh rằng AGa, BGb, CGc, DGd đồng qui.
B
Giải
Gọi M, N, p là trung điểm của CD, DB, BA.	c
Trong mp(MAB): AGa n BGb = I.
Ta có:	= 3 => BA // GAGB
mga mgb . A B
Vậy AIAB đồng dạng với AIGaGb
IA _ IB AB .
IGa ■ IGb ■ GaGb
Lại có AMAB đồng dạng với AMGbGa
=> —= 3	(2)
gagb mgb
Từ (1) và (2), ta có:	- -7^- = 3
iga igb
Chứng minh tương tự, ta cũng có
IB _ IC _3và IC _ ID
igb igc igc igd
Vậy các đường trên đồng qui tại điểm xác định I.
Bài 5. Cho tứ giác ABCD nằm trong mặt phẳng (a) có hai cạnh AB và CD không song song với nhau, s là điểm nằm ngoài mặt phẳng (a) và M là trung điểm của đoạn sc.
Tìm giao điểm N của đường thẳng SD và mặt phẳng (MAB).
Gọi o là giao điểm của AC và BD. Chứng minh rằng ba đường thẳng SO, AM và BN đồng quy.
cần nhớ
A e d c mp(a) => A e mp(a)
Giải
Tìm N e SD n mp(MAB)
Trong mp(ABCD), AB cắt CD tại I
Trong mp(SCD), IM cắt SD tại N.
Ta có:
N 6 SD
. Ne IM c mp(MAB)
=> N e mp(MAB)
Vậy N = SD n mp(MAB)
Chứng minh so, MA, BN đồng quy
Ta có:
* SO, MA, BN không ở trong cùng một mặt phẳng
SO và MA cắt nhau (trong mp(SAC)
MA và BN cắt nhau (trong mp(AIN)
BN và SO cắt nhau (trong mp(SBD)
Vậy SO, MA, BN đồng quy.
Bài 6. Cho bôn điểm A, B, c và D không đồng phảng. Gọi M và N lần lượt là trung điểm của các đoạn thẳng AC và BC. Trên đoạn BD lấy điểm p sao cho BP = 2PD.
Tìm giao điểm của đường thẳng CD và mặt phẳng (MNP).
37
Tìm giao tuyến của hai mặt phẳng (MNP) và (ACD).
Ta có:
BN _ 1. BP _ 2
BC - 2 ; BD “ 3
BN BP
BC * BD
=> NP và CD không song song với nhau
=> NP và CD cắt nhau tại E.
E e NP => E € (MNP).
Mà E e CD
Vậy E e CD n (MNP)
Trong mặt phẳng (ACD) thì AD và ME cắt nhau tại điểm Q.
Q E AD Q e (ACD)
Q e ME => Q e (MNP)
Vậy Q là một điểm chung của hai mặt phảng (ACD) và (MNP).
Ta đã có M là một điểm chung của hai mặt phẳng (ACD) và (MNP).
Vậy MQ = (ACD) n (MNP).
Bài 7. Cho bốh điểm A, B, c và D không đồng phẳng. Gọi I, K lần lượt là trung điểm của AD và BC.
Tìm giao tuyến của hai mặt phẳng (IBC) và (KAD).
Gọi M và N là hai điểm lần lượt lấy trên hai đoạn thẳng AB và AC. Tìm giao tuyến của hai mặt phẳng (IBC) và (DMN).
Giải
a) Tìm giao tuyến của mp(IBC) và mp(KAD).
Ta có:
(K G BC => K e (IBC)
I e AD => I e (KAD)
Vậy KI = (IBC) n (KAD)
b) Trong mp(ABD): BI n DM = p p e (IBC) n (DMN)
Do (DMN) = (DMC)
=> c e (IBC) n (DMN)
Vậy (IBC) n (DMN) = PC
Bài 8. Cho tứ diện ABCD. Gọi M và N lần lượt là trung điểm của các cạnh AB và CD, trên cạnh AD lấy điểm p không trùng với trung điểm của AD.
Gọi E là giao điểm của đường thẳng MP và đường thẳng BD. Tìm giao tuyến của hai mặt phẳng (PMN) và (BCD).
Tìm giao điểm của mặt phảng (PMN) và BC.
Giải
Trong mp(ABD):
MP không song song với
MP n BD = E
E G MP => E G (PMN)
E G BD => E G (BCD)
Nên E G (PMN) n (BCD)
Mà N G (PMN) n (BCD)
Nên EN = (PMN) n (BCD)
Trong mp(BCD): EN n BC = F
Mà (PMN) = (MEN) EE (MEF)
=> F G (MEF) = (PMN)
Mặt khác F G BC nên F = BC n (PMN)
Bài 9. Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Trong mặt phẳng (ABCD) vẽ đường thẳng d đi qua A và không song song với các cạnh của hình bình hành, d cắt BC tại E. Gọi C’ là một điểm nằm trên cạnh sc.
Tìm giao điểm M của CD và mp (C’AE).
Tìm thiết diện của hình chóp cắt bởi mặt phẳng (C’AE).
Giải
a) Giao điểm M của CD và mp(CAE).
Trong mp (ABCD), d cắt CD tại M, ta có:
M G CD
M G d c (C’AE)
=> M G (C’AE)
Vậy M là giao điểm của CD và mp (C’AE).
b) Thiết diện của hình chóp cắt bởi mp(C’AE).
Trong mp(SCD), MC’ cắt SD tại K.
Vậy thiết diện của hình chóp S.ABCD cắt bởi mp (C’AE) là tứ giác AKC’E.
Bài 10. Cho hình chóp S.ABCD có AB và CD không song song. Gọi M là một điểm thuộc miền trong của tam giác SCD.
Tìm giao điểm N của đường thẳng CD và mp(SBM).
Tìm giao tuyến của hai mặt phẳng (SBM) và (SAC).
Tìm giao điểm I của đường thẳng BM và mặt phẳng (SAC).
Giải
Tìm giao điểm p của sc và mp(ABM), từ đó suy ra giao tuyến của hai mặt phẳng (SCD) và (ABM).
Gọi N là giao điểm của SM và CD, thì N = CD n (SBM).
Trong mp(ABCD), BN và AC cắt nhau tại điểm o.
o e BN o e (SBM)
0 e AC => o e (SAC)
=> o là một điểm chung của (SBM) và (SAC)
Dễ thấy s cũng là một điểm chung của (SBM) và (SAC).
Vậy SO = (SBM) n (SAC).
Trong mp (SBM) thì BM và so cắt nhau tại điểm I. ta có
I G BM => I e so => I (= (SAC). Vậy I = BM n (SAC).
Trong mp (SAC), AI cắt sc tại o, ta có p e sc và p e AI.
=> p e (ABM) hay p là giao điểm của mp (ABM) với cạnh sc của hình chóp.
Trong mp (SCD), PM cắt SD ở điểm Q, ta có Q e SD; Q e PM mà PM e (ABM)
=> Q e (BM) hay Q là giao điểm của mp (ABM) với cạnh SD của hình chóp. Vậy: (SCD) n (ABM) = PQ.