Giải bài tập Toán 11 Bài 2. Hai đường thẳng vuông góc

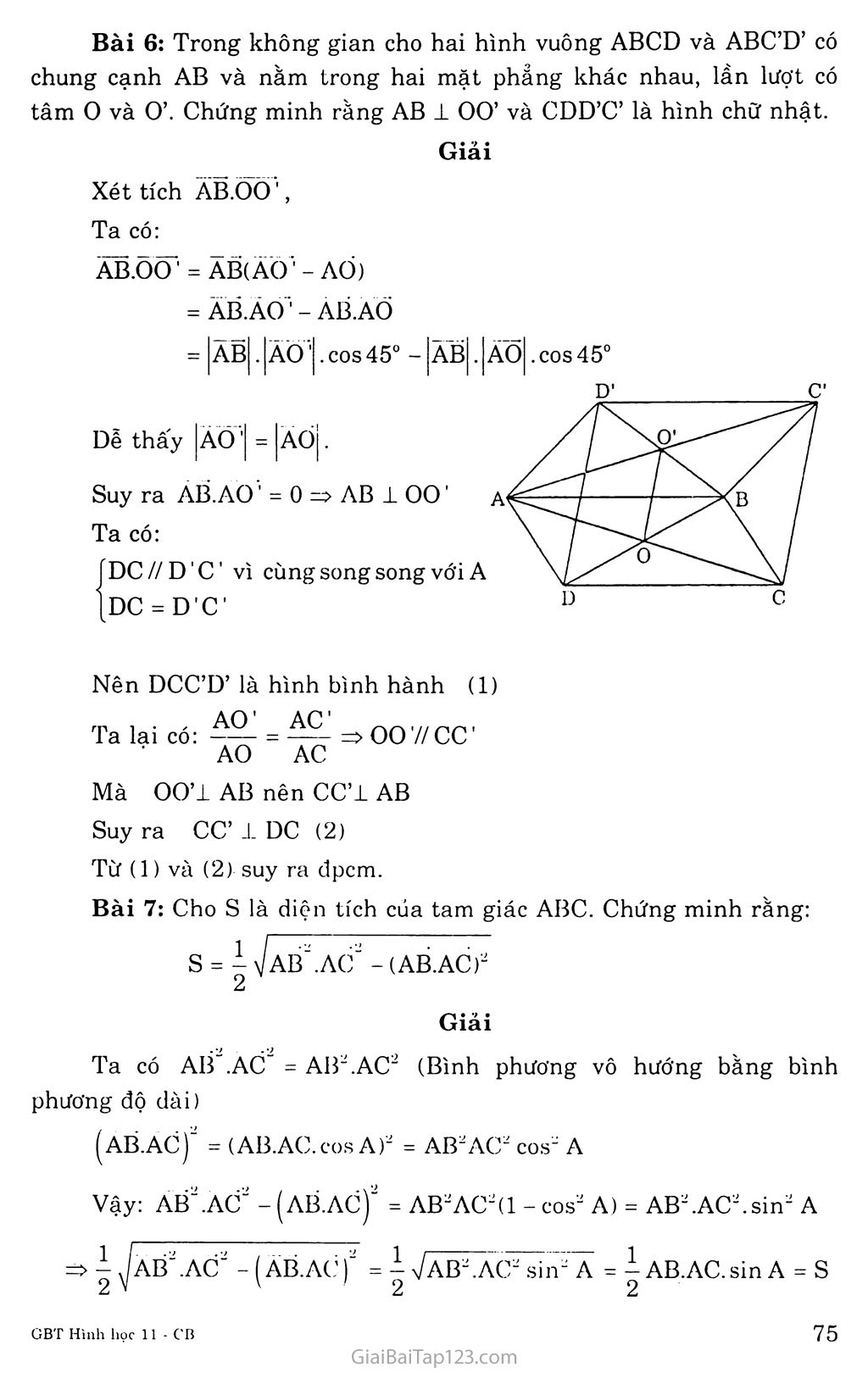
Bài 2. HAI ĐƯỜNG THẮNG VUÔNG GÓC
A. KIẾN THỨC CẦN NAM vững
I. Vectơ chỉ phương của đường thẳng
Định nghĩa
Vectơ ã khác vectơ 0 được gọi là vectơ chỉ phương của đường thẳng d nếu giá của vectơ ã song song hoặc trùng với đường thẳng d.
Tính chất
Nếu ã là vectơ chỉ phương của đường thẳng d thì vectơ kã với k 0 cũng là vectơ chỉ phương của d. Tất cả các vectơ chỉ phương của đường thẳng d đều cùng phương.
Một đường thẳng d trong không gian hoàn toàn được xác định nếu biết một điểm A thuộc d và một vectơ chỉ phương á của nó.
b’
b
Góc giữa hai đường thẳng bất kì trong không gian
Định nghĩa: Góc giữa hai đường thẳng a, b là góc của hai đường thẳng song song với a và b, kí hiệu là (a, b) hay (b, a).
Chú ỷ: Để xác định (a, b) ta có thể lấy điểm o nằm ngay trên một trong hai đường thẳng đó.
Hai đường thẳng vuông góc
Định nghĩa: Hai đường thẳng gọi là vuông góc với nhau nếu góc giữa chúng bằng 90°.
Như vậy: a ± b (a, b) = 90°.
Liên hệ giữa quan hệ song song và quan hệ vuông góc của hai đường thẳng
Định lí: Cho hai đường thẳng song song. Đường thẳng nào vuông góc với đường thẳng thứ nhất thì vuông góc với đường thẳng thứ hai.
Tức là:
ía // b
=> c 1 b.
[c 1 a
Chú ý:
Trong không gian, hai đường thẳng vuông góc thì hoặc cắt nhau hoặc chéo nhau.
Trong mặt phẳng, hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì song song với nhau, nhưng trong không gian thì không còn đúng.
B. HƯỚNG DẪN GIẢI BÀI TẬP
Bài 1: Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa các cặp vectơ sau đây:
AB và EG b) AF và EG c) AB và DH
Giải
Đ
a) Góc giữa AB, EG
EG = AC => (AB, eg) = (ÃB, ÁC) = BAG
Mà ABCD là hình vuông nên BAG = 45"
Vậy (AB, eg) = 45°
b) Góc giữa AF, EG
EG = AC => (AF, eg) = (AF, AC) = FAC
AC, AF, FC là các đường chéo hình vuông bằng nhau nên bằng nhau Vậy A AFC đều nên FAC = 60°
Do đó (AF, eg) = 60°
Góc giữa AB và DH
DH = AẺ nên (ÁB, Dli) = (AB, ÃỂ) = 90"
Bài 2: Cho tứ diện ABCD
Chứng minh rằng AB.CD + AC.DB + AD.BC = 0. (1)
Từ đẳng thức trên hãy suy ra rằng nếu ABCD có AB 1 CD và AC 1 DB thì AD 1 BC.
Giải
Đưa các vecto’ có cùng gốc A, ta có:
AB.CD = AB (ad - AC) = ÃB.ÃD - AB.AC
< AC.DB = AC (AB - AD) = AB. AC - AC. AD
AD.BC = AD (AC - AỖ) = ÃC.ÃD - AB.AD
Cộng cậc đẳng thức trên ta được: AB.CD + ÃC.DB + AD.BC = 0
Do AB 1 CD nên AB.CD = 0
Do AC 1 DB nên AC.DB = 0
Thay vào đẳng thức (1) ta được: 0 + 0 + AD.BC = 0 => AD 1 BC
Bài 3:
Trong không gian nếu hai đường thẳng a và b cùng vuông góc với đường thẳng c thì a và b có song song với nhau không?
Trong không gian nếu đường thẳng a vuông góc với đường thẳng b và đường thầng b vuông góc với đường thẳng c thì a có vuông góc với c không?
Giải
Trong không gian nếu hai đường thẳng a và b cùng vuông góc với đường thẳng c thì nói chung a và b không song song với nhau vì a và b có thể cắt nhau hoặc có thể chéo nhau.
Trong không gian nếu a 1 b và b 1 c thì a và c vẫn có thê’ cắt nhau hoặc chéo nhau do đó, nói chung a và c không vuông góc với nhau.
Bài 4: Cho hai tam giác điều ABC và ABC’ trong không gian nói chung cạnh AB và nằm trong hai mặt phẳng khác nhau. Gọi M, N, p và Q lần lượt là trung điểm của các cạnh AC, CB, BC’ và C’A.
Chứng minh rằng:
AB 1 CC’
Tứ giác MNPQ là hình chữ nhật.
Giải
Đặt AB = a, ta có AC = BC = AC’ = BC’ = a
Chứng minh AB 1 CC’
Ta có:
AB.CC ’= AB.(AC - AC)
= AB.AC' - ÁB.AC
AB.AC = AB.AC.cos(AB.AC)
- a.a.cos60” -
2
AB.AC = AB.AC.cos(AB.AC) = a.a.cos60° =
2
Vậy AB.CC = -a- - y = 0 => AB 1 CC’ (dpcm)
Chứng minh MNPQ là hình chữ nhật
MN là đường trung bình của tam giác ABC => MN = -gAB (1)
2
QP là đường trung bình của tam giác ABC’ => QP = AB (2)
2
(1) và (2) -> MN - QP
=> MNPQ là hình bình hành (3)
Ta có MN // AB và NP // CC’ mà AB 1 CC’ nên MN 1 NP (4)
Từ (3) và (4), suy ra MNPQ là hình chữ nhật (đpcm)
Bài 5: Cho hình chóp tam giác S.ABC có SA - SB - sc và có
ASB = BSC - CSA . Chứng minh rằng SA 1 BC, SB 1 AC, sc 1 AB.
Giải
SA.SC SA.SC. cos(SÁ.SC) = a" cosa
SẤ.SC ~ SA.SB. cos(SA.SB) = a~ cosa B
Vậy SẤ.BCÌ 0 SA . BC (đpcm)
Chung minh tương tự ta cũng có SB 1 AC và sc 1 AB
Bài 6: Trong không gian cho hai hình vuông ABCD và ABC’D’ có chung cạnh AB và nằm trong hai mặt phẳng khác nhau, lần lượt có tâm 0 và O’. Chứng minh rằng AB 1 00’ và CDD’C’ là hình chữ nhật.
Giải
Xét tích ÂB.ÕÕ',
Ta có:
ÃB.ÕÕ’ = ÃỖCÀO ■' - AÓ)
= AB.A0' - AB.A0
= |ÃỖ|.IAO'1. cos 45° - |ab| .|ÃỒ|.cos 45°
ư	 C’
Dễ thấy |ÃÕ'| = |Ã0|.	z71	I
Suy ra AB.A0’’ = 0 => AB 1 00'	A	/
Ta có:	\	\ /
. \ / \/
j DC // D1 c ’ vì cùng song song với A
[DC = D’C’	D	c
Nên DCC’D’ là hình bình hành (1)
AO' AC
Ta lại có: 4^- = ^5-	00 7/ cc ’
■ AO AC
Mà 00’1 AB nên CC’l AB
Suy ra CC’ 1 DC (2)
Từ (1) và (2) suy ra đpcm.
Bài 7: Cho s là diện tích cúa tam giác ABC. Chứng minh rằng:
S = ịựABJ.AC’ -(AB. AC)2
2
Giải
Ta có AB .AC = A1T.AC2 (Bình phương vô hướng bằng bình phương độ dài)
(AB.AC)2 = (AB.AC.cosA)2 = AB2AC2 cos2 A
Vậy: AB'.AC2 -(abac)2 = AB2AC2(1 - cos2 A) = AB2.AC2.sin2 A => ị Jab' .AC' - I AB.AC )■ = ị VÃB^Ãcrlĩirà = ị AB.AC. sin A = s
2V	\	’	2	2
Bài 8: Cho tứ diện ABCD có AB = AC = AD và BAC = BAD = 60°
Chứng minh rằng:
AB 1 CD
Nếu M, N lần lượt là trung điểm của AB và CD thì MN 1 AB và MN 1 CD
Giải
Đặt AB = AC = AD = a
Ta có:
AB.AC = AB(AD - AC) - AB. AD - AB. AC
= a.a.cos60° - a.a.cos60° = 0
=> AB 1 CD
* Ta co: MN = MA + AD + DN (1)
Và MN = MB + BC + CN (2)
(1)+ (2)ta được:
2MN = (mà + mb) + AD + BC + (DN + CN)
2MN = 0 I AD i BC + 0 = AD + BC
Từ đó:
AB.(2MN) = AB (ad + BC) = Ali.AD + AB.BC - AB.AD - BA.BC
Mà A ABC đều nên: AB.(2MN) = a.a.cos60° - a.a.cos60° = 0
Vậy: AB.(2MN) = 2AB.MN = 0 => AB 1 MN
* MN.CD = j(AD + BC)CD = |(AD + AC +AB)(Ãĩj-ÃC)
2	2	.
= ị (ADJ - AC.AD 4- ACAD - AC' - ABAC + abac)
2\	I
= ị (AD" - AC2 - ABAC + ABAC)
2 \	)
- (a2 - a2 - a.a cos 60° + a.a cos 60°) = 0
=> MN 1 CD