Giải bài tập Toán 11 Bài 3. Đường thẳng vuông góc với mặt phẳng

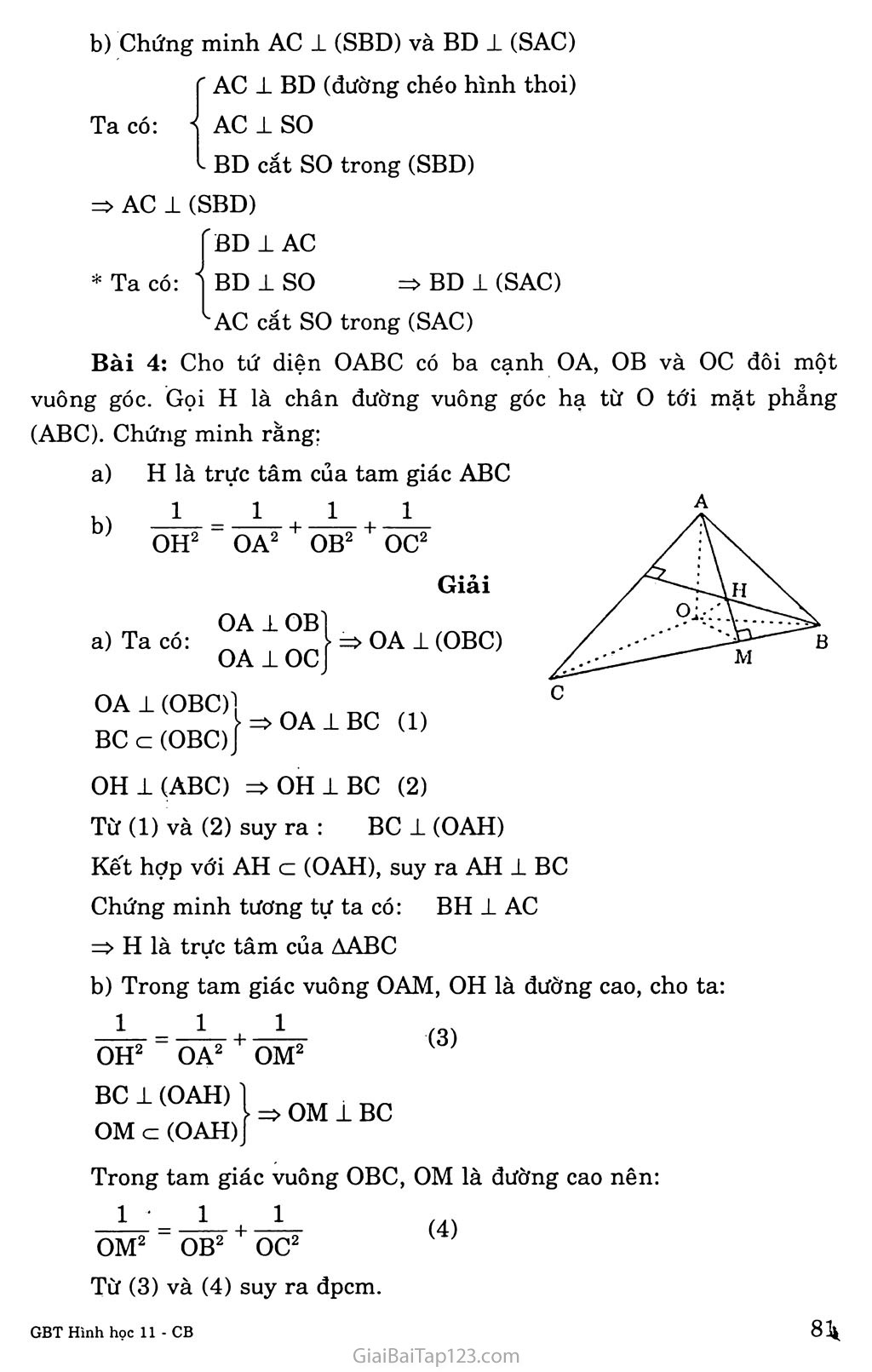
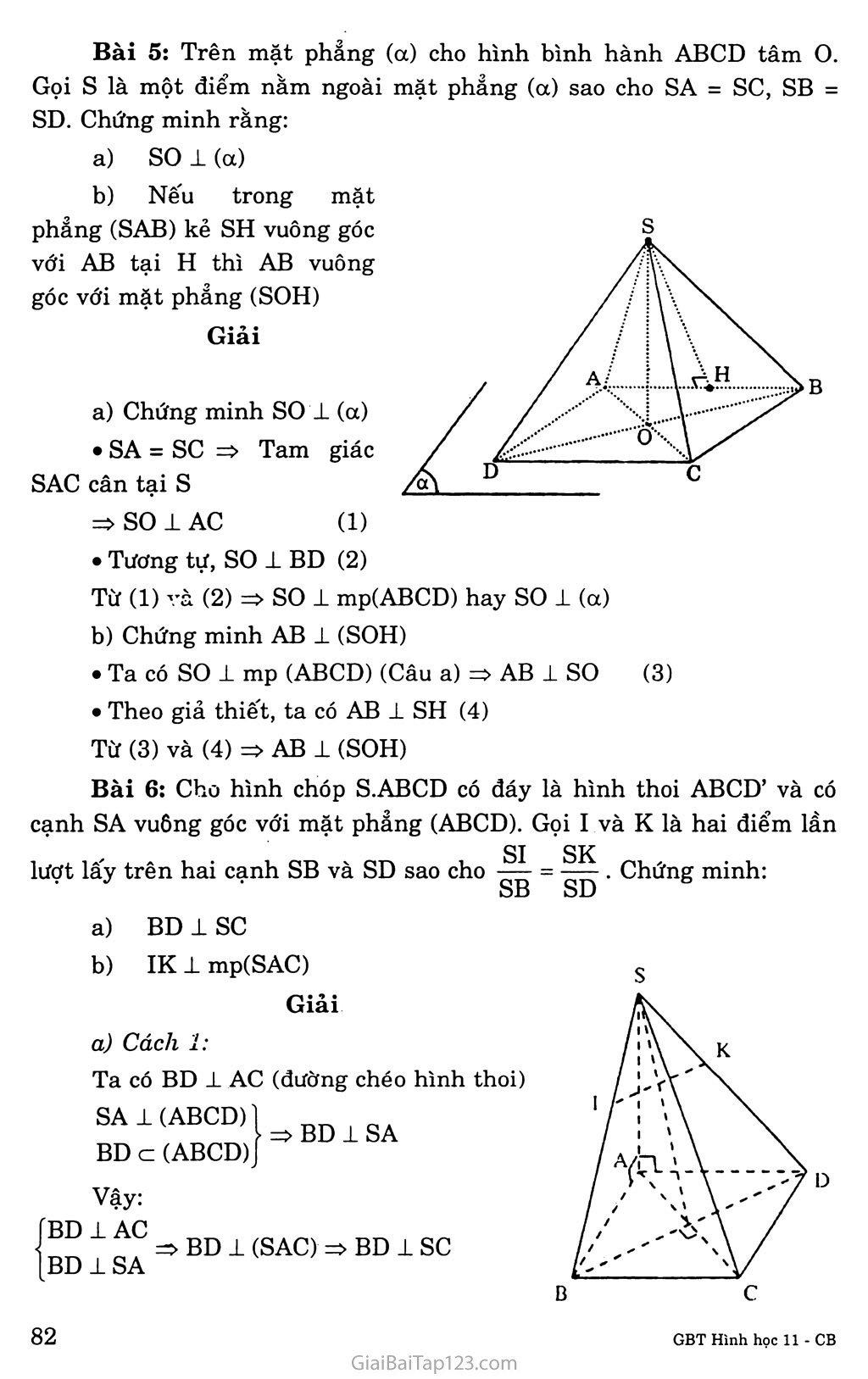
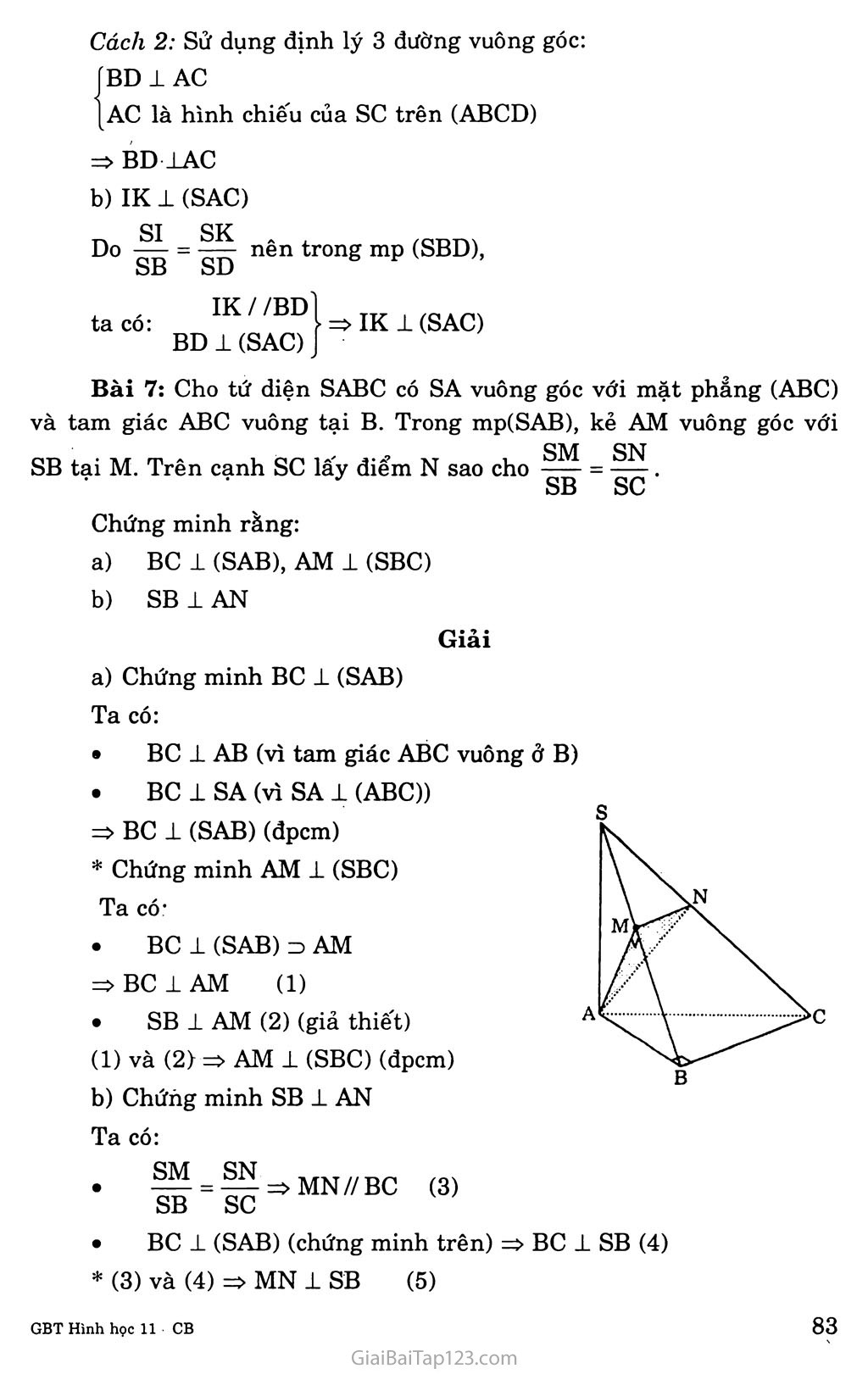
Bài 3. ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHANG
A. KIẾN THỨC CẦN NAM vững
I. Đường thẳng vuông góc với mặt phẳng:
a) Định nghĩa-. Nếu đường thắng d vuông góc với mọi đường thẳng thuộc mặt phẳng (P) thì đường thẳng d được gọi là vuông góc với mặt phẳng (P).
d t ... .3 _	,n J => d 1 (P)
m là đường thăng bất kỳ thuộc (P)J
Định lí: Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b của mặt phẳng (P) thì d vuông góc với mặt phẳng (P).
d ± a
=> d 1 (P)
d lb anb í ộ a; b c (P)
Định lý 2: Qua một điểm o cho trước có một và chỉ một mặt phẳng vuông góc với đường thẳng A cho trước.
vectơ pháp tuyến cúa mặt
Định lí 3: Qua một điểm o cho trước có một và chí một đường thẳng vuông góc với một mặt phẳng (P) cho trước.
II. Vectơ pháp tuyến của mặt phang
1. Định nghĩa
Vecto' ri khác vectư 0 được gọi là phẳng a nếu giá của ri vuông góc với a.
Tính chất
a) Nếu ri là vectơ pháp tuyến của mặt phẳng a thỉ kri với k * 0 củng là một veclơ pháp tuyến của mặt phang dó.
Nếu mặt phang a có cặp vectơ cliỉ ph ương \ả, bị và nhận ri làm vectơ pháp tuyến thì ri . á = 0 và ri . b = 0.
Sự liên quan giữa hệ vuông góc và quan hệ song song
a) Mặt phẳng nào vuông góc với một trong hai đường thẳng song song thì cũng vuông góc với dường thẳng kia.
Đường thẳng nào vuông góc với một trong hai mặt phẳng song song thì cũng vuông góc với mặt phẳng kia.
Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
Xác định mặt phẳng vuông góc với dường thẳng và đường thẳng vuông góc với mặt phẳng.
Định lí 3
Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.
Hệ quả
Một mặt phẳng hoàn toàn được xác định nếu biết một điểm và một vectơ pháp tuyến của mặt phẳng đó.
Mặt phẳng trung trực của một đoạn thẳng
Người ta gọi mặt phẳng a đi qua trung điểm của đoạn thẳng AB và vuông góc với đoạn thẳng AB là mặt phảng trung trực của đoạn AB.
Nếu a là mặt phảng trung trực của đường thẳng AB ta có:
M e a MA = MB
Định lí 4
Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phảng cho trước.
1 M
Phép chiếu vuông góc
1. Định nghĩa: Phép chiếu song song trong đó phương chiếu vuông góc với mặt chiếu gọi là phép chiếu vuông góc.
Chú ỷ: Phép chiếu vuông góc có đầy đủ các tính chất của phép chiếu song song.
Định lí (Định lí ba đường vuông góc): Cho đường thẳng a không vuông góc với mặt phẳng oc. Một đựờng thẳng b nằm trong a vuông góc với đường thẳng a khi và chỉ khi b vuông góc với hình chiếu của a trên a.
Tức là, với a’ lè hình chiếu vuông góc của a lên a thì: a ± b C7 a a’ ± b.
Góc giữa đường thẳng và mặt phẳng
Định nghĩa.
Cho đường thẳng d cắt mặt phảng a tại điểm o và không vuông góc với cc. Góc giữa đường thẳng d và mặt phảng a là góc tạo bởi đường thẳng d và hình chiếu vuông góc d’ của d trên mặt phẳng a và được kí hiệu là (đ, cộ .
• Nếu d vuông góc với a, ta quy ước id, aj = 90°.
• Nếu d // cc hay d nằm trong a, ta quy ước (d, a) = 0°.
Chú ý: Nếu d không vuông góc với a ta có (d, cộ = (d, d'j. Trong trường hợp này ta lấy một điểm A tùy ý trên d, khác với điểm o và gọi H là hình chiếu vuông góc của điểm A trên mặt phảng a.
Khi đó ta có (d, cộ = AOH.
B. HƯỚNG DẪN GIẢI BẤI TẬP
Bài 1: Cho mặt phảng (a) và hai đường thẳng a, b.
Các mệnh đề sau đây đúng hay sai?
Nếu	a	// (a), b	± (a) thì a 1 b.
Nếu	a	// (a), b	1 a thì b 1 (a).
Nếu	a	// (a), b	// (a) thì b // a.
Nếu	a	1 (a), b	1 a thì b 1 (a).
Giải
a) Đúng	b) Sãi
Sai	d) Sai
Giải thích:
• a // (a) => a // a’c (a) (1)
• b 1 (a) => b 1 a’ (2)
* (1) và (2) => a ± b
fa //(a)
4) 1 a
Điều này chưa đủ đế b _L (cc)
• a // (a) => a // a’c (a)
• b // (a) => b // b’c (a)
a’ và b’ có thể cắt nhau nên
a và bước có thể chéo nhau
a i (a) và b 1 a thì b có thể nằm trong mp(a)
Bài 2: Cho tứ diện ABCD có hai mặt ABC và BCD là hai tam giác cân có chung đáy BC. Gọi I là trung điểm của cạnh BC.
Chứng minh rằng BC vuông góc với mặt phẳng (ADI)
Gọi AH là đường cao của tam giác ADI, chứng minh rằng AH vuông góc với mặt phẳng (BCD)
Giải
a) AABC cân tại A => AI 1 BC. Tương tự AI 1 BC.
AI 1BC'
DI1BC
=> BC 1 (AID)
b)
BC 1 (ADI)
AH 1 (ADI)
=> AH 1 BC
AH1BC
AH1DI
=> AH 1 (BCD)
í SO 1 AC
SAC, SBD nên: s so 1 BD
1 AC A BD = o
Bài 3: Cho hình chóp S.ABCD có đáy là hình thoi ABCD tâm 0 và có SA = SB = SC = SD. Chứng minh rằng:
a) Đường thẳng so vuông góc với mặt phảng (ABCD)
b) Đường thẳng AC vuông góc với mặt phẳng (SBD) và đường thẳng BD vuông góc với mặt phảng (SAC)
Giải
a) Chứng minh so 1 (ABCD)
SO là trung tuyến của hai tam giác cân
=> SO 1 (ABCD)
b) Chứng minh AC ± (SBD) và BD 1 (SAC)
' AC 1 BD (đường chéo hình thoi)
Ta có: 5 AC 1 so
- BD cắt SO trong (SBD)
=> AC 1 (SBD)
CbD 1 AC
* Ta có: BDiSO
=> BD 1 (SAC)
lAC cắt SO trong (SAC)
Bài 4: Cho tứ diện OABC có ba cạnh OA, OB và oc đôi một vuông góc. Gọi H là chân đường vuông góc hạ từ o tới mặt phảng (ABC). Chứng minh rằng:
H là trực tâm của tam giác ABC
1 - 1	1	1
OH2 OA2 + OB2 + oc2
Giải
a) Ta có:
OA 1 OB
OA 1 oc
OA 1 (OBC)Ị
BCc(OBC)]
=> OA 1 BC (1)
=> OA 1 (OBC)
OHl(ABC) OH 1 BC (2)
Từ (1) và (2) suy ra : BC 1 (OAH)
Kết hợp với AH c (OAH), suy ra AH 1 BC
Chứng minh tưorng tự ta có: BH 1 AC
=> H là trực tâm của AABC
b) Trong tam giác vuông OAM, OH là đường cao, cho ta:
1 1 1
0H2 ÕÃ7 0M2
BC 1 (OAH)
OM c (OAH)
1 => OM 1BC
(3)
Trong tam giác vuông OBC, OM là đường cao nên:
1.1 1 OM2 " OB2 + oc2
Từ (3) và (4) suy ra đpcm.
(4)
Bài 5: Trên mặt phẳng (a) cho hình bình hành ABCD tâm o. Gọi s là một điểm nằm ngoài mặt phẳng (a) sao cho SA = sc, SB = SD. Chứng minh rằng:
SO 1 (a)
Nếu trong mặt phảng (SAB) kẻ SH vuông góc với AB tại H thì AB vuông góc với mặt phảng (SOH)
Giải
a) Chứng minh so ± (a)
• SA = sc => Tam giác SAC cân tại s
=> SO 1 AC	(1)
• Tương tự, SO 1 BD (2)
(3)
Từ (1) và (2) => SO 1 mp(ABCD) hay so 1 (a) b) Chứng minh AB 1 (SOH)
• Ta có SO 1 mp (ABCD) (Câu a) => AB 1 so
• Theo giả thiết, ta có AB 1 SH (4)
Từ (3) và (4) => AB 1 (SOH)
Bài 6: Cho hình chóp S.ABCD có đáy là hình thoi ABCD’ và có cạnh SA vuông góc với mặt phẳng (ABCD). Gọi I và K là hai điểm lần
SI SK
lượt lấy trên hai cạnh SB và SD sao cho —. Chứng minh:
■ ử	■	SB SD
a) BD 1 sc
b) IK 1 mp(SAC)
Giải
Ta có BD ± AC (đường chéo hình thoi)
SAKABCD)'
BD c (ABCD)
) => BD 1 SA
a) Cách ỉ:
Vậy:
RD I AC
_ *" BD 1 (SAC) => BD 1 sc BD ISA
Cách 2: Sử dụng định lý 3 đường vuông góc:
BD 1 AC
AC là hình chiếu của sc trên (ABCD)
=> BD 1AC
b) IK 1 (SAO
Do	nên trong mp (SBD),
SB SD	6
IK//BD
ta có:	
BD 1 (SAO
Bài 7: Cho tứ diện SABC có SA vuông góc với mặt phẳng (ABC) và tam giác ABC vuông tại B. Trong mp(SAB), kẻ AM vuông góc với SB tại M. Trên cạnh sc lấy điểm N sao cho	.
SB sc
Chứng minh rằng:
BC 1 (SAB), AM 1 (SBC)
SB 1 AN
Giải
a) Chứng minh BC 1 (SAB)
Ta có:
• BC 1 AB (vì tam giác ABC vuông ở B)
BC 1 SA (vì SA 1 (ABO) => BC ± (SAB) (đpcm)
Chứng minh AM 1 (SBC)
Ta có.'
BC 1 (SAB) z> AM
=> BC 1 AM (1)
SB 1 AM (2) (giả thiết)
(1) và (2)=> AMI (SBC) (đpcm) b) Chứng minh SB ± AN
Ta có:
SB SC
BC ± (SAB) (chứng minh trê
B
=> BC 1 SB (4)
* (3) và (4) => MN 1 SB (5)
* Theo giả thiết, ta có AM 1 SB (6)
Từ (5) và (6), suy ra SB 1 (AMN) => SB 1 AN (đpcm).
Bài 8: Cho điểm s không thuộc mặt phẳng (a) có hình chiếu trên (a) là điểm H. Với điểm M bất kì trên (a) và không trùng với H, ta gọi SM là đường xiên và đoạn HM là hình chiếu của đường xiên đó.
Chứng minh rằng:
Hai đường xiên bằng nhau khi và chỉ khi hai hình chiếu của chúng bằng nhau;
Với hai đường xiên cho trước, đường xiên nào lớn hơn thì có hình chiếu lớn hơn và ngược lại, đường xiên nào có hình chiếu lớn hơn thì lớn hơn.
Giải
a) Giả sử ta có hai đường xiên SA, SB và các hình chiếu HA, HB
của chúng trên mp(a)
• Giả sử HA = HB
ASHA = ASHB => SA = SB
Vì SH 1 mp(a) nên SH 1 HA và SH _L SB và các tam giác SHA, SHB là các tam giác vuông. Hai tam giác vuông SHA, SHB có cạnh SH chung và HA = HB nên.
• Ngược lại nếu SA = SB thì ASHA = ASHB ha = HB
Kết quả, ta có HA = HB SA = SB (đpcm)
b) Giả sử có hai đường xiên SA, SC và các hình chiếu HA, HC của chúng trên mp(a) với giả thiết HC > HA.
Trên đoạn HC, lấy điểm B’ sao cho HA’ = HA => HC > HA’. Như vậy, theo kết quả câu a) ta có SA’ = SA. Ta có trong các tam giác vuông SHB’, SHC thì:
SC2 = SH2 + HC2
SA2 = SH2 + HA2
Vì HC > HA’ nên sc2 > SA2 => sc > SA
Suy ra sc > SA
Như vậy HC > HA => sc > SA
Lí luận tương tự, ta có:
Kết quả: HC > HA 
SC > SA => HC > HA
sc > SA