Giải bài tập Toán 11 Bài 5. Khoảng cách

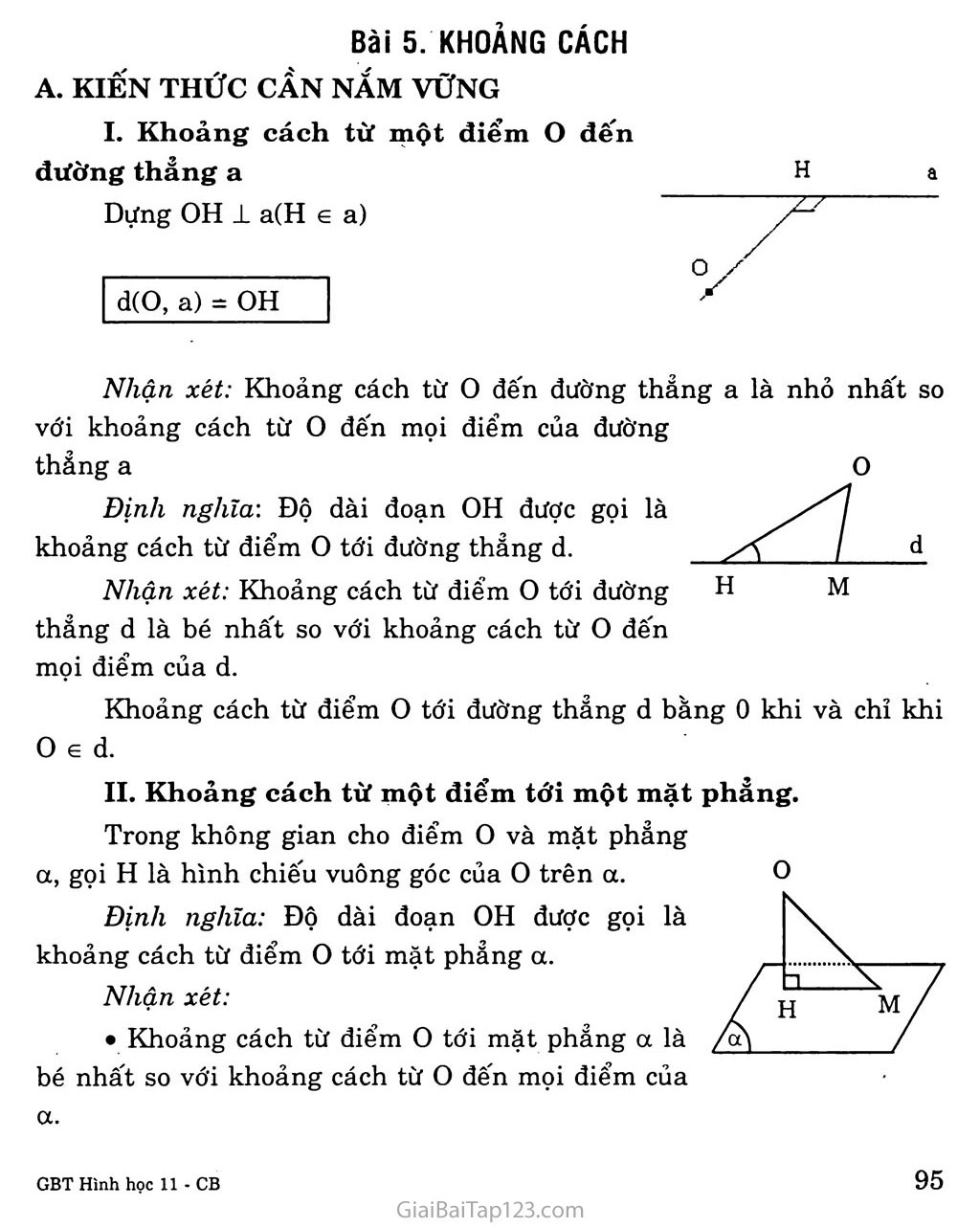
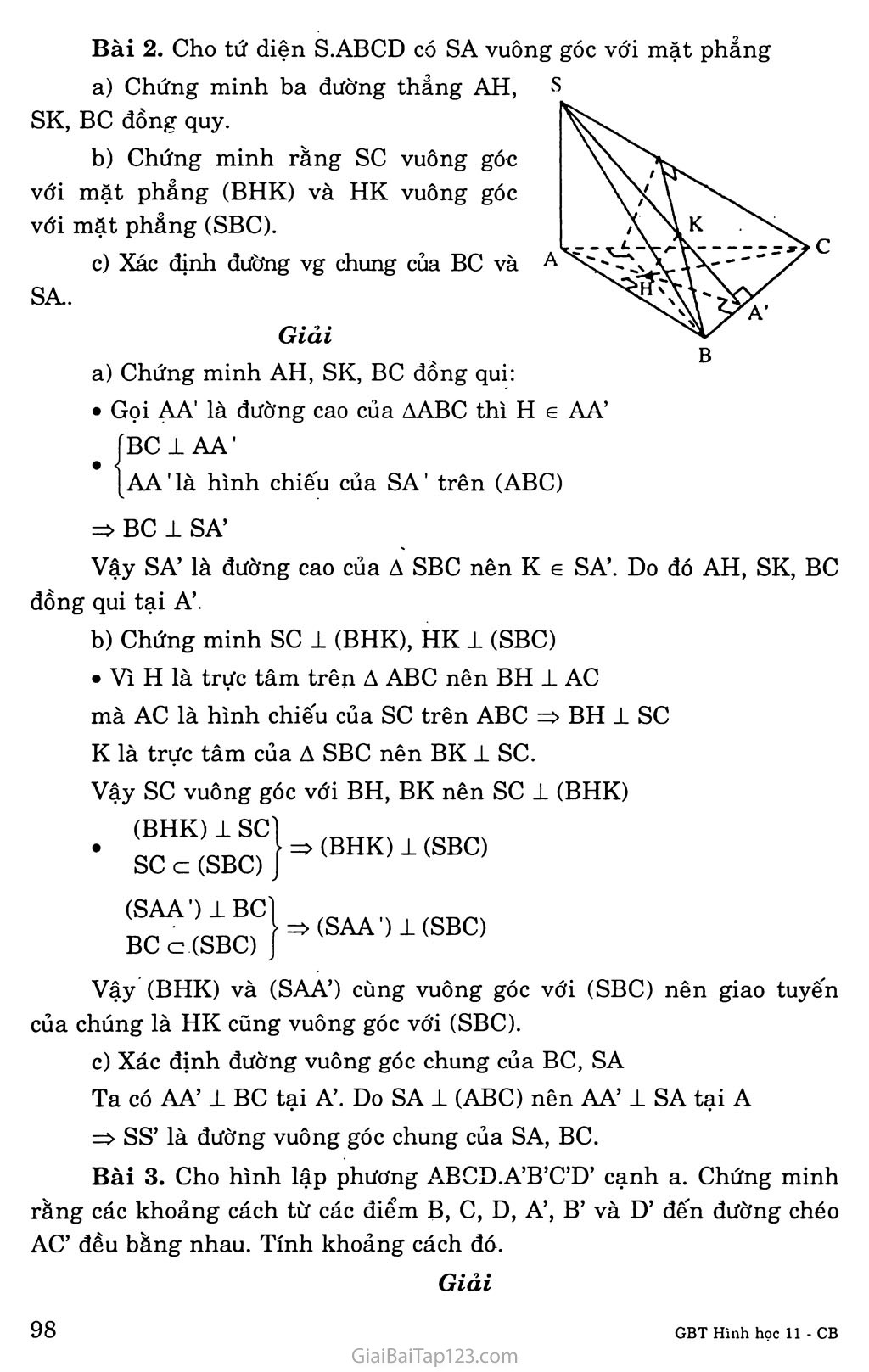
o.
Bài 5. KHOẢNG CÁCH
A. KIẾN THỨC CẦN NAM vững
I. Khoảng cách từ một điểm o đến đường thẳng a
Dựng OH 1 a(H e a)
d(O, a) = OH
Nhận xét: Khoảng cách từ o đến đường thẳng a là nhỏ nhất so
với khoảng cách từ o đến mọi điểm của đường thẳng a
Định nghĩa’. Độ dài đoạn OH được gọi là khoảng cách từ điểm o tới đường thẳng d.
o
M
Nhận xét: Khoảng cách từ điểm o tới đường H thẳng d là bé nhất so với khoảng cách từ o đến
mọi điểm của d.
Khoảng cách từ điểm o tới đường thẳng d bằng 0 khi và chỉ khi 0 e d.
II. Khoảng cách từ một điểm tới một mặt phẳng.
Trong không gian cho điểm o và mặt phảng a, gọi H là hình chiếu vuông góc của o trên cc.
Định nghĩa: Độ dài đoạn OH được gọi là khoảng cách từ điểm o tới mặt phẳng a.
Nhận xét:
• Khoảng cách từ điểm o tới mặt phẳng a là bé nhất so với khoảng cách từ o đến mọi điểm của
a.
• Khoảng cách từ điểm o tới mặt phảng a bằng 0 khi và chỉ khi o e a
Khoảng cách từ một đường thẳng và một mặt phẳng
song song.
Trong không gian cho đường thẳng d song song với mặt phẳng a. Lấy điểm A bất kì trên d, gọi H là hình chiếu vuông góc của A trên a.
Định nghĩa: Độ dài đoạn AH được gọi là khoảng cách từ đường thẳng d tới mặt phẳng a.
Nhận xét: Khoảng cách từ đường thẳng d tới mặt phảng a là bé nhất so với khoảng cách từ một điểm tùy ý thuộc d tới mọi điểm bất kì của cc.
Khoảng cách giữa hai mặt phẳng song song
Trong không gian cho hai mặt phẳng a, p song song với nhau.
Định nghĩa: Khoảng cách từ một điểm tùy ý của a tới p được gọi là khoảng cách giữa hai mặt phẳng a và p.
Nhận xét: Khoảng cách giữa hai mặt phẳng a, p là bé nhất so với khoảng cách từ một điểm tùy ý thuộc a tới một điểm bất kì của p.
Đường vuông góc chung và khoảng cách giữa hai đường thẳng chéo nhau.
Định lí: Cho hai đường thẳng chéo nhau a và b, luôn có duy nhất một đường thẳng d cắt cả a và b và vuông góc với mỗi đường thẳng ấy. Đường thẳng d được gọi là đường vuông góc chung của a và b.
Giả sử d cắt a, b theo thứ tự tại M và N.
Định nghĩa-. Đoạn MN được gọi là đoạn vuông góc chung của a và b. Độ dài đoạn thẳng MN được gọi là khoảng cách giữa hai đường thẳng chéo nhau a và b.
Nhận xét: Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa:
Một trong hai đường thẳng đó và mặt phẳng song song với nó chứa đường thẳng còn lại.
Hai mặt phẳng song song chứa hai đường thẳng đó.
Từ đó suy ra: “Khoảng cách giữa hai đường thẳng chéo nhau là bé nhất so với khoảng cách giữa hai điểm bất kỳ lần lượt nằm trên hai đường thẳng ấy”.
B. HƯỚNG DẪN GIẢI BÀI TẬP
Bài 1.'Trong các mệnh đề sau đây mệnh đề nào là đúng?
Đường thẳng A là đường vuông góc chung của hai đường thẳng a và b nếu Ala và Aỉb.
Gọi (P) là mặt phảng song song với cả hai đường thẳng a và b chéo nhau thì đường vuông góc chung của a và b luôn luôn vuông góc với (P).
Gọi A là đường vuông góc chung của hai đường thẳng chéo nhau a và b thì A là giao tũyến của hai mặt phẳng (a, A) và (b, A).
Cho hai đường thẳng chéo nhau a và b. Đường thẳng nào đi qua một điểm M trên a đồng thời cắt b tại N và vuông góc với b thì đó là đường vuông góc chung của a và b.
Đường vuông góc chung A của hai đường thẳng chéo nhau a và b nằm trong mặt phẳng chứa đường này và vuông góc với đường kia.
Giải
Sai. đúng là “Đường thẳng A là đường thẳng vuông góc chung của hai đường thẳng chéo nhau a và b nếu 4 cắt cả a và b, đồng thời A lavàAlb.”
Đúng	c) Đúng
Sai	e) Sai.
Bài 2. Cho tứ diện S.ABCD có SA vuông góc với mặt phẳng
Chứng minh ba đường thẳng AH, SK, BC đồng quy.
Chứng minh rằng sc vuông góc với mặt phảng (BHK) và HK vuông góc với mặt phẳng (SBC).
Xác định đường vg chung của BC và SA..
Giải
a) Chứng minh AH, SK, BC đồng qui:
Gọi AA' là đường cao của AABC thì H e AA’
BC1AA'
<
AA'là hình chiếu của SA' trên (ABC)
=> BC 1 SA’
Vậy SA’ là đường cao của A SBC nên K e SA’. Do đó AH, SK, BC đồng qui tại A’.
Chứng minh sc 1 (BHK), HK 1 (SBC)
• Vì H là trực tâm trên A ABC nên BH ± AC
mà AC là hình chiếu của sc trên ABC => BH ± sc
K là trực tâm của A SBC nên BK 1 sc.
Vậy sc vuông góc với BH, BK nên sc ± (BHK)
=> (BHK) 1 (SBC)
(BHK) 1 sc
sc c (SBC)
=>(SAA') l(SBC)
(SAA') 1BCÌ
BC c.(SBC) J
Vậy (BHK) và (SAA’) cùng vuông góc với (SBC) nên giao tuyến của chúng là HK cũng vuông góc với (SBC).
Xác định đường vuông góc chung của BC, SA
Ta có AA’ 1 BC tại A’. Do SA 1 (ABC) nên AA’ 1 SA tại A
=> SS’ là đường vuông góc chung của SA, BC.
Bài 3. Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Chứng minh rằng các khoảng cách từ các điểm B, c, D, A’, B’ và D’ đến đường chéo AC’ đều bằng nhau. Tính khoảng cách đó.
Giải
Các tam giác BAC’, CA’A, DAC’, A’AC, B’C’A, D’C’A bằng nhau nên các đường cao ứng với cạnh AC’ bằng nhau.
Ta có CC’ = a ; CA = aự2
1 11
CH2 - cc12 + AC2
0.7«
Từ đây ta tính được CH = —
J	3
Bài 4. Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = b,
CC’ = c.
a) Tính khoảng cách từ B đến mặt phảng (ACC’A’).
b) Tính khoảng cách giữa hai đường thẳng BB’ và AC’.
H
Giải
Ta có: AA’ 1 (ABCD)
AA’ c (ACC’A’)
=> (ACC’A’) 1 (ABCD)
Hai mặt phảng này vuông góc với nhau và cắt nhau theo giao tuyến AC nên nếu từ B ta kẻ BH 1 AC thì BH 1 (ACC’A’) và BH là khoảng cách từ B đến mp (ACC’A’)
Ta có AC2 = a2 + b2 => AC = yja2 + b2
Ta lại có BH.AC = BA.BC (= 2Sabc) => BH = B^BC- => BH = ab
AC T^Tb7
b) (ACC’A’) o AC mà CC’ // BB’ nên BB’ // (ACC’A’)
Mặt phảng (ACC’A’) chính là mặt phảng chứa A’C’ và song song với BB’; B là một điểm thuộc BB’, do đó khoảng cách BH từ B đến mp (ACC’A’) cũng là khoảng cách giữa hai đường thẳng BB’ và A’C’ và eũngtòng-^.
Bài 5. Cho hình lập phương ABCD.A’B’C’D’
Chứng minh rằng B’D vuông góc với mặt phẳng (BA’Ơ)
Tính khoảng cách giữa hai mặt phảng (BA’C’) và (ACD)
Tính khoảng cách giữa hai đường thẳng BC’ và CD’.
Giải
Chứng minh B’D 1 (BA’C’):
* Cách 1. Ta có BD là đường chéo của hình chữ nhật BB’D’D và hình chữ nhật AB’C’D
m , A'C'lB’D'i
Ta có: , _,
A'C'IDD' Ị
=> A’C-1 (BB’D’D) => A’C’ 1 B’D
Tương tự : A’B 1 (AB’C’D) => A’B 1 B’D => B’D 1 (BA’Ơ)
* Cách 2. D.BA’C’ và B’.BA’C’ là các hình chóp đều có chung mặt đáy là A BA’C’. Gọi I là tâm của tam giác BA’C’ thì DI ± (BA’C’) và BT 1 (BA’C’) => B, I, D thẳng hàng và B’D ± (BA’C’)
có :
Khoảng cách giữa (BA’C’), (ACD’)
BA 7/ CD ’■
BC7/AD'
(BA’C')//(ACD')
Ta
Gọi o, O’ là tâm của ABCD, A’B’C’D’
và gọi I, J lần lượt là tâm của hai tam giác đều BA’C’ và ACD’.
Xét hình chữ nhật BBD’D’D ta có BO’ // OD’ nên
OJ là đường trung bình của A DBI nên IJ = JD. 10’ là đường trung bình của A B’JD nên IJ = BI => BI = IJ = JD = |b’D
3
Theo câu trên B’D 1 (BA’C) nên IJ 1 (BA’C’)
Mà J é (ACD’) nên khoảng cách giữa 2 mặt phẳng song song (ACD’) và (BA’C’) là độ dài IJ.
Và IJ = 4b'D = 4VB’B2+ BD2 =ịjĩ
3	3	3’
Bài 6. Chứng minh rằng nếu đường thẳng nối trung điểm hai cạnh AB và CD của tứ diện ABCD là đường vuông góc chung của AB và CD thì AC = BD và AD = BC.
100
Giải
* Thực hiện phép đốì xứng trục Đij, ta có:
[A->B ÍAC = BD
!._	(đpcm)
[c -> D [AD = BC F
Bài 7. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 3a, cạnh bên bằng 2a. Tính khoảng cách từ s tới mặt đáy (ABC).
Giải
• Gọi o là tâm của đáy ABC (O là trọng tâm, trực tâm của tam giác ABC)
• S.ABC là hình chóp đều => so 1 (ABC)
Tam giác SAO vuông ở o
=> SO2 = SA2 - AO2 với:
SA = 2a
.AO^AM-ị^-aVã
3	3	2
=> SO2 = 4a2 - 3a2 = a2 so = a
Vậy khoảng cách từ s tới mp(ABC) bằng a.
Bài 8. Cho tứ diện ABCD cạnh a. Tính khoảng cách giữa hai cạnh đối diện của tứ diện đều đó.
Giải
Gọi M là trung điểm AB và N là trung điểm CD
MN = 7bN2 - BM2 = . Ííặ-T - f =
vl 2 I l2j \ 4
Vậy d(AB, CD) = MN =