Giải toán 11 Bài 2. Giới hạn của hàm số
§2. GIỚI HẠN CỦA HÀM số
A. KIẾN THỨC CÃN BẢN
GIỚI HẠN HỮU HẠN CỦA HÀM số TẠI MỘT ĐIEM
Định nghĩa
Cho khoảng K chứa điểm Xo và hàm số y = f(x) xác định trên K hoặc trên K \ {Xo}.
Ta nói hàm số y = f(x) có giới hạn là số L khi X dần tới Xo nếu với dãy số (xn) bất kì, xn e K \ {x0} và xn -> x0, ta có f(xn) dần tới L.
Kí hiệu: lim f(x) = L hay f(x) -> L khi X -> x0.
x->Xg
Định lí về giới hạn hữu hạn
Định lí
Giả sử lim f(x) = L và lim g(x) = M. Khi đó
X—>Xq X—>Xq
lim [f(x) + g(x)] = L + M;
x-»x0
. lim [f(x) - g(x)] = L - M; x-»x0
. lim [f(x).g(x)] = L.M;
x->x0
f(x) L
lim -7-7 = 7“ (nếu M * 0). x->x0 g(x) M
Nếu f(x) > 0 và lim f(x) = L, thì L > 0 và lim Jf(x) = 7Ĩ .
X->x0 X—»xg
(Dấu của f(x) được xét trên khoảng đang tìm giới hạn với X * x0).
Giới hạn một bên
Cho hàm sô' y = f(x) xác định trên khoảng (x0; b).
Số L được gọi là giới hạn bên phải của hàm số y = f(x) khi X -> Xo nếu với dãy số (xn) bất kì, Xo x0, ta có f(xn) -> L.
Kí hiệu lim f(x) = L.
X-»Xq
Cho hàm số f(x) xác định trên khoảng (a; x0).
Số L được gọi là giới hạn bên trái của hàm số y = f(x) khi X -> x0 nếu với dãy số (xn) bất kì, a x0, ta có f(xn) -> L.
Kí hiệu lim f(x) = L. x->x0
Định lí: lim f(x) = L khi và chỉ khi lim f(x) = lim f(x) = L.
X-»Xg x-»xỏ X->xj
GIỚI HẠN HỮU HẠN CỦA HÀM số TẠI VÔ cực
Định nghĩa
Cho hàm số y = f(x) xác định trên khoảng (a; +oo).
Ta nói hàm sô' y = f(x) có giới hạn là số L khi X -> +00 nếu với dãy số (xn) bất kl, xn > a và xn -> +00, ta có f(xn) -» L.
Kí hiệu lim f(x) = L hay f(x) -> L khi X -> +00.
X—>+00
Cho hàm sô' y =f(x) xác định trên khoảng (-oo; a).
Ta nói hàm sô' y = f(x) có giới hạn là sô' L khi X -» -00 nếu với dãy sô' (xn) bất kì, xn -00, ta có f(xn) -> L.
Kí hiệu lim f(x) = L hay f(x) -> L khi x -> -00.
X—>—<30
GIỚI HẠN VÔ cực CỦA HÀM số
Giới hạn vô cực
Định nghĩa: Cho hàm sô' y - f(x) xác định trên khoảng (a; +oo).
Ta nói hàm sô' y = f(x) có giới hạn là -00 khi X -> +00 nếu với dãy sô' (xn) bất kl, xn > a và xn -> +00, ta có f(xn) -> -00.
Kí hiệu lim f(x) = -00 hay f(x) -> -00 khi X -> +00.
X—»+co
Nhận xét: lim f(x) = +00 lim (-f(x)) = -00.
X->+cc X—>+<o
Các giới hạn đặc biệt
lim xk = +00 với k nguyên dương.
X—>+<30
lim xk = -00 nếu k là sô' lẻ.
X—>—<30
lim xk = +00 nếu k là sô' chẵn.
X->—00
Các quy tắc tìm giới hạn
lim f(x) x-»x0
lim g(x) x->x0
lim f(x).g(x) x-»xg
L > 0
+00 '
+ 30
-00
-00
L < 0
+00
-00
-00
+00
lim f(x) x-»x0
lim g(x)
x-»x0
Dấu của g(x)
.. f(x) lim -f-i x->x0 g(x)
L
±00
Tùy ý
0
L > 0
0
+
+00
-
-00
L < 0
+
-00
-
+00
2-5xà các dãy số (Un) với u„ = - ; (vn) với Vn = .
n n
c. PHƯƠNG PHÁP GIẢI BÀI TẬP
1. Dùng định nghĩa, tim các giới hạn sau: x + 1
a) lim
X-.4 3x - 2 '
b) lim
x->«c x + 3
£jtải
a) Xét hàm số f(x) =
x + 1
3x - 2
có tập xác định
D = K\ ± ±;+00 ;x = 4 e
Giả sử (xn) là dãy số bất kì với xn > ; xn í 4 và x„ 4 khi n -> +00.
3
2-5xTính limUn, limVn, limf(Un) và limf(Vn).
Từ đó có kết luận gi về giới hạn của hàm số đã cho khi X -> 0?
„ xác định trên K. x2 + 3
Giả sử (xn) là dãy số bất kì, xn -> +x khi n +00.
2 - 5x2 X2 - 5
Ta có limílXn) = lim—° = lim „ = -5.
b) Hàm sô' f(x) =
4+3
VA i;~ 2-5x2
Vậy lim —-- ■■ = -5.
*-»+« X2 + 3
Cho hàm số f(x) = nếux>0
[2x nê’ux<0
(sjiai
limVn = liml - —I =0.
Ta có limun = lim— = 0;
n
Do un = — > 0 và vn = <0, nên f(un) = /— + 1 và f(vn) = - —.
n .11 V n n
Từ đó: limf(un) = lim
— + 11=1; n
limf(vn) = lim— = 0.
Vi un -» 0 và vn -> 0, nhưng limflUn) * limf(vn) nên hàm số f(x) không có giới hạn khi X —> 0.
Tính các giới hạn sau:
a) lim
X ->-(
d) lim
3 X + 1
2x-6
4 - X
b) lim
X-.-;
e) lim
4-xz 2 X + 2
17
c) lim
Jx + 3 - 3
.6 X - 6
-2xz + X -1
a) Ta có lim
x2-l
x->-3 X +
x--'X ^1
ỐịiẦi
f) lim
X-XWC 3 + X
-- = lim (x -1) = -3 -1 = -4
1 x-x-3
4 - X2
lim = lim(2-x)=4
X—»—2 X + 2 X—*—2
. 1. Vx + 3 - 3 .
lim —-— = lim
x->6 x-6
(x + 3)-9 ' 1 1
m . . , 7 = lim . —- = —
*6 (x - 6)(\/x + 3 + 3) x~*6 Vx + 3 +3 6
d) lim 4—- = lim
x-»+x 4 — X x->+co
XR) 2~x 2
\ 4 = lim = 4 = -2
17
Vì lim (X2 + 11 = +00 nên lim ——— = 0
0 lim '•'•y ‘ - lim
x-x+oo 3 + X X—»+x
X -2 +
11 X X2
..I 3 , ,
XI - + 1
X
X—>+co \ ' x-*+co + 1
-2 +-2+ 4
= lim X —-—— = -00 (vì lim X= +00 và lim —-—— = -2 < 0).
X—»+cO O X—»+cC X—>+CC O „
- +1 — + 1
X X
4. Tìm các giới hạn sau: 3x-5
a) lim
X—»2
(x-2)2
. . , 2x-7 2x-7
t>) lim ■ ; c) lim ——7-.
X-.1- X - 1 X -1
Ốịiảí
lim(3x -5)= 1 > 0; lim(x - 2)2= 0 và (x - 2)2 > 0, Vx * 2
X—»2 ’ x-»2 7
3x-5
=> lim—- - = +0O
*“2(x-2)2
lim (2x - 7) = -5 lim -X - 7 = +00.
x-»r X-»J- ' x“i X -1
,. / _ 2x — 7
lim (2x - 7) = -5 0 => lim ——— = -00
x-»i+ X-»1+ x-r X -1
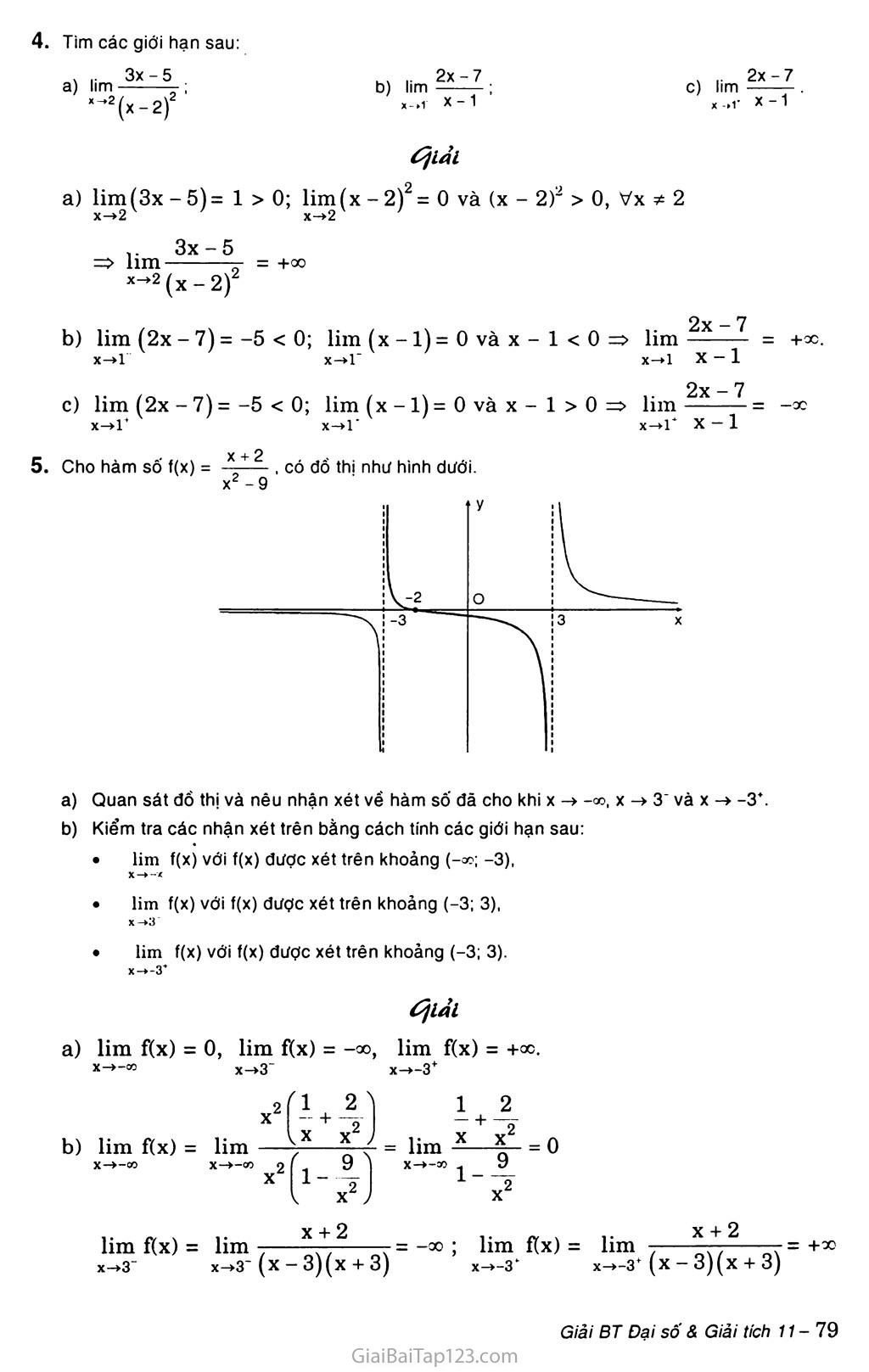
5. Cho hàm số f(x) = * + 2 , có đồ thị như hình dưới.
X2 - 9
Quan sát đồ thị và nêu nhận xét vể hàm số đã cho khi X -> -a>, X -> 3' và X -» -3‘.
Kiểm tra các nhận xét trên bằng cách tính các giới hạn sau:
lim f(x) với f(x) được xét trên khoảng (-»; -3),
x-»-x
lim f(x) với f(x) được xét trên khoảng (-3; 3),
x->3’
• lim f(x) với f(x) được xét trên khoảng (-3; 3).
ỐỊiải
a) lim f(x) = 0, lim f(x) = -00, lim f(x) = +oc. x->-=0 x-»3“ x->-3+
*1
'1 2Ì <x + X2 J
X2
1-1
l X2 J
x“b-+-2i 1+4
b) lim f(x) = lim ——^-4- = lim ——= 0
X—>—00 X-»-cc 9 ( 9 I X—>—co - y
x 1--J
lim f(x) = lim x->3_
= +»
=-00 ; lim fíx) = lim .
x~3* (x - 3)(x + 3) x”-3* x-»-3+(x - 3)(x + 3)
Tính: a) lĩm (X -Xc + X-1); C) lim vx -2X + Õ
X-++X X->-X
t>) lim (—2x3 + 3x2 - 5) d) lim + 1 .
X—»-x X—>+« 5 - 2x
ốịlẦi
lim (x4 - X2 + X - 1) = lim X4 11 -1= +C0
X—»+co X—>+cc ỵ x^ XJ X? J
(vì lim X4 = +00 và lim I 1 - + “3 - Ậ I = 1 > 0)
X->+cc X—>+ce Ỳ X* X X4 /
lim (-2x3 + 3x2 - 5) = lim xs(-2 + — - -^-) = +00
X->-co X->-00 X
(vì lim X3 = -00 và lim (-2 + — - -^-) = -2-00 X
lim 7x2 - 2x + 5 = lim |x| /1- — + -^- =+00
X—00 x->-oo Y X x^
I 2 5-
(vì lim Ixl = +00 và lim 1 - — + —r = 1 > 0)
X-+-CŨ X—>—00 ỵ X X
= -l.
.„ 77TĨ.X x ? ■ x‘ •1 .... fĩ
-2
x^»+M 5 - 2x x-»+<o (5
7. Một thấu kính hội tụ có tiêu cự là f. Gọi d và d' lần lượt là khoảng cách từ một vật thật AB và từ ảnh A'B’ của nó tới quang tâm o cùa thấu kính.
Công thức thấu kinh là 4 + 37= / ■ d d' f
X -- - 2
í d d'
1« - *1«--
Tìm biểu thức xác định hàm số d' = <p(d).
Tim lim (d) và lim <p(d). Giải thích ý nghĩa của các kết quả tìm được.
d->f* d->f" d~>+'
éỹlải
a) Từ hệ thức 3- + 37 = 3 suy ra: d' = tp(d) = tá J d d' f d-f
b) • lim <p(d) = lim
J .r+ ' ' .f+
fd
d->r ' ’ d->f+ d - f
= +00.
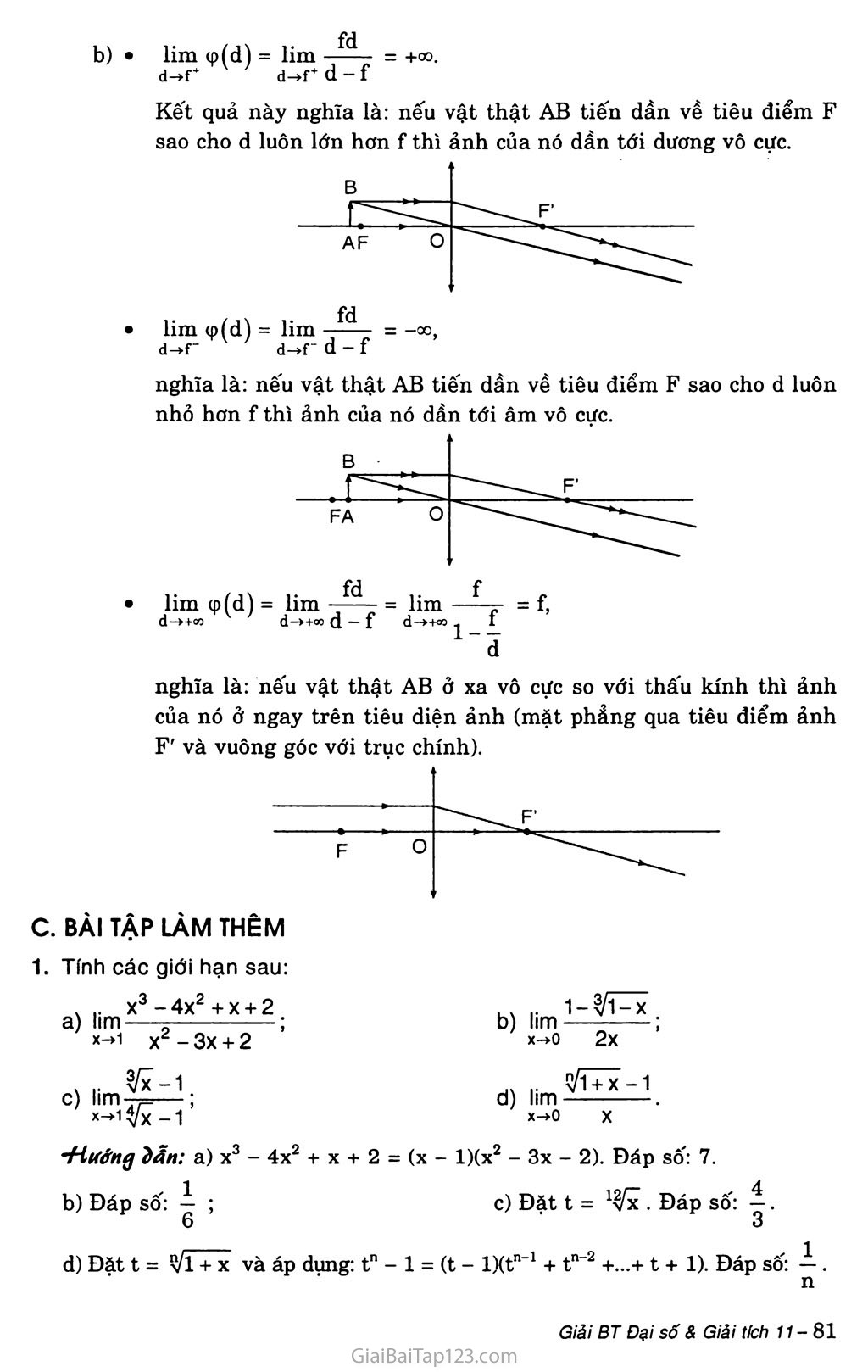
Kết quả này nghĩa là: nếu vật thật AB tiến dần về tiêu điểm F sao cho d luôn lớn hơn f thì ảnh của nó dần tới dương vô cực.
nghĩa là: nếu vật thật AB tiến dần về tiêu điểm F sao cho d luôn nhỏ hơn f thì ảnh của nó dần tới âm vô cực.
d-*+co
nghĩa là: nếu vật thật AB ở xa vô cực so với thấu kính thì ảnh của nó ở ngay trên tiêu diện ảnh (mặt phẳng qua tiêu điểm ảnh F' và vuông góc với trục chính).
c. BÀI TẬP LÀM THỀM
1. Tính các giới hạn sau: X3 -4x2 +X + 2
a) lim
X->1 X - 3x + 2
b) lim
x-»0 2x
5/1 +- X — 1
c lim ; x-ii/x-1
-Hướng ìẫn: a) X3 - 4x2 + X + 2 = (x - l)(x2 - 3x - 2). Đáp số: 7.
d) lim x-»ỏ
b) Đáp sô': ;
c) Đặt t = . Đáp số: .
3
Đặt t = 3/l + x và áp dụng: tn - 1 = (t - l)(tn_1 + tn’2 +...+ t + 1). Đáp số: .
n
2. Tính các giới hạn:
Đáp số: a)
X -1
lim——— X-»1 x" -1
n(n-l)
—— •
X -nx + n-1 b) lim- ——
X-»1 x-1
Vx2 +1
b) lim ịx-Vx2 +5x );
X—>+cc \ /
Tính các giới hạn:
a) .Iim -
X'Ạ+Kx + 1 + Vx2 +1
lim ỉ7x2 +1 - >Jx3 -ì) .
X—>+cc \ /
Đáp số: a) — ;
2
Tìm các giới hạn sau:
a) lim (-3x3 + 4x2 - 2x + 1);
X—»-oo
. 5x~1.
lim
X-»1 1-x
ĐS: a) +oo; b) +oo;
Tlm các giới hạn sau:
, 3x 2
a) lim - ; ;
X_>_1(x + 1) (x-2)
0.
b) lim A?2x4 -2x-1
X—>—00
.. 5x-1
lim--—-.
X—>1 1-X
c) -oo; d) +oo;
b) lim- ——- — .
*->-1(x+ 1)(X2 -2x + 3)
ĐS: a) +oo;
b) -00.