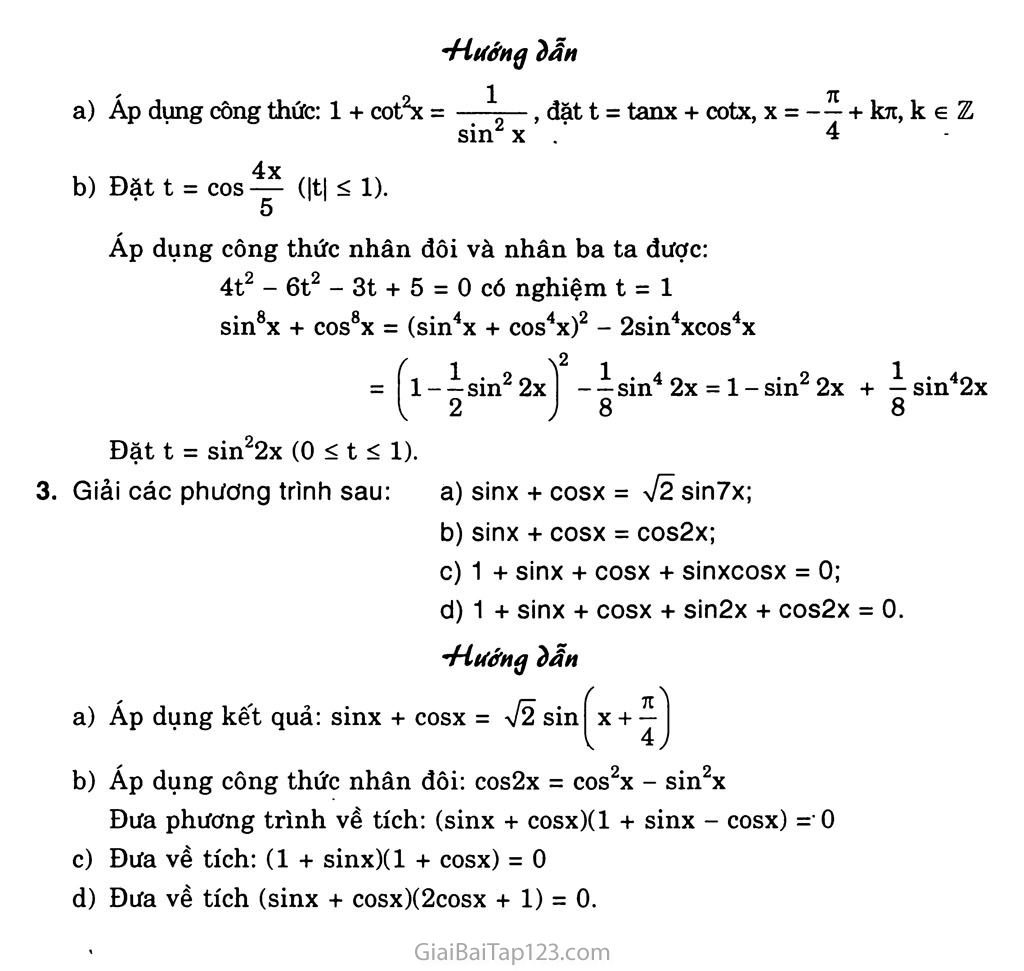Giải toán 11 Bài 3. Một số phương trình lượng giác thường gặp

§3. MỘT SỐ PHƯƠNG TRÌNH LƯỢNG GIÁC
THƯỜNG GẶP
A. KIẾN THỨC CĂN BẢN
PHƯƠNG TRÌNH BẬC NHẤT Đốl VỚI MỘT HÀM số LƯỢNG GIÁC
.Phương trình bậc nhất đối với một hàm số lượng giác là phương trình có dạng
at + b = 0 (a * 0)	(1)
trong đó a, b là các hằng số, t là một trong các biểu thức sinx, cosx, tanx hoặc cotx.
Cách giải: Chuyển vế rồi chia hai vế của phương trình (1) cho a ta đưa phương trình (1) vể phương trình lượng giác cơ bản.
PHƯƠNG TRÌNH BẬC HAI ĐÔÌ VỚI MỘT HÀM số LƯỢNG GIÁC
Phương trình bậc hai đối với một hàm số lượng giác là phương trình có dạng
at2 + bt + c = 0 (a * 0)
trong đó a, b, c là các hằng số và t là một trong các biểu thức sinx, cosx, tanx hoặc cotx.
Cách giải: Đặt biểu thức lượng giác làm ẩn phụ và đặt điều kiện cho ẩn phụ (nếu có) rồi giải phương trình theo ẩn phụ này. Cuối cùng ta đưa về việc giải các phương trình lượng giác cơ bản.
PHƯƠNG TRÌNH BẬC NHẤT Đốl VỚI SINX VÀ cosx
asinx + bcosx = c (1) (a2 + b2 * 0)
Cách giải thứ nhất: Chia hai vế phương trình cho Va2 + b2 ta được:
a 	 b .	c
,	cos X + ,	sinx = ,
Va2 +b2 Va2 + b2 Va2 +b2 Đặt , a =CQS(p thì , b =sin<p
* V^Tb^
Đưa phương trình về dạng:
COSXCOSỌ + sinxsincp -	, c hay cos(x - ọ) = -. c =
Điều kiện có nghiêm:
 c A = a + b - c2 > 0
7a2+b2	7a2+b2
Va2 + b2
_ .	,,	c
Gọi a là cung sao cho cosa =
Va2 +b2
Ta có: cos(x -ọ) = cosa X = ọ ± a + k2rc
,	X
Cách giải thứ hai: Dùng ẩn phụ t = tan (x * 71 + k2n)
Trước hết xem X = 7T + k2n có là nghiêm không. Nếu có ta nhận đó là một nghiêm. Nêu X = 71 + k27t không là nghiêm thì đặt t = tan ~ .
1-t2
Giải phương trình cơ bản tan-| = ti; tan-|= t2
B. PHƯƠNG PHÁP GIẢI BÀI TẬP
1. Giải phương trình: sin2x - s1nx = 0.
ốịíài
sin2x - sinx = 0 sinx(sinx - 1) = 0 
2. Giải các phương trình: a) 2cos2x - 3cosx +1=0;
a) Đặt t = cosx; -1 < t < 1
Ta có 2t2 - 3t + 1 = 0 
sin X = 0 sinx = 1
X = kĩt
X = 7- + k2n. 2
b) 2sin2x + V2sin4x = 0.
(k e Z)
Ốịlải
't = 1
cosx = 1
1 
1 
t = -
cosx = —
2
L	2 L
X = k2ĩi
X = ±-^ + k2rc.
3
(k e Z)
b) 2sin2x + 72 sin4x = 0 2sin2x(l + 72 cos2x) = 0 sin2x = 0
cos2x = -
72 
x = k-.
2'
X = ±—- + krc.
8
(k e Z)
3. Giải các phương trình:
a) sin2 - 2cos^ + 2 = 0;
2 2
2tan2x + 3tanx +1=0;
b) 8cos2x + 2sinx -7 = 0;
tanx - 2cotx +1=0.
Ốjiải
a) sin24-2cos^ + 2 = 0 1 - cos2^-2cos^ + 2 = 0 cos2^ + 2cos; 2	2	2	2	2	í
cos^ = l
 ^ = k2rc X = k4ĩt (k G Z)
cos^ = -3 (loại)
ỵ ’
‘b) 8cos2x + 2sinx - 7 = 0 8(1 - sin2x) + 2sinx -7 = 0
 8sin2x - 2sinx - 1 = 0 
sin x = 4 2
sin X = - -
L'
X = -^ + k2n; X =	+ k2ji
6 6
X = arcsin I - 4 I + k2ĩi; X = n - arcsin
(k e Z)
+ k2n
tan X = -1
c) 2tan2x + 3tanx + 1 = 0 
X = - — + kĩt,
4
tan X = —
X = arctan -4 + krr.
2.
't = 1
tan X = 1
t =-2
tan X = -2
L
X = -7 + krt
4
X = arctan (-2) + krt
4. Giải các phương trinh:
a) 2sin2x + sinxcosx - 3cos2x = 0;
(k e Z)
c) sin2x + sin2x - 2cosJx = 4 ;
2
tan X = 1
2tan2x + tanx - 3 = 0 
tan X = —
3 !
X = — + kĩi
4
X = arctan
(-1)
(k G Z)
+ k?t
b) Ta có với cosx = 0 thì sin2x = 1 nên giá trị X mà cosx = 0 không thỏa mãn phương trình. Chia hai vê phương trình cho cos2x * 0 ta được
3tan2x - 4tanx + 5 = 2( 1 + tan2x)
 tan2x - 4tanx + 3 = 0 
tan X = 1 tan X = 3
X = -7 + krc
4	(k e Z)
X = arctan 3 + kn
Đặt t = tanx ta có phương trình t - — + l = 0t2 + t- 2 = 0 t
b) 3sin2x - 4sinxcosx + 5cos2x = 2;
2cos2x - 3 Ự3 Sin2x - 4sin2x = -4.
íìiẰi
Ta có với COSX = 0 thì sin2x = 1 nên giá tri X mà cosx = 0 không thỏa mãn phương trình. Chia hai vê phương trình cho cos2x * 0 được
Ta có với sin2x + sin2x - 2cos2x = Ậ sin2x + 2sinxcosx - 2cos2x = —
2
Giá trị X mà cox = 0 không thỏa mãn phương trình. Chia hai vê phương trình cho COS2X * 0 ta được:
2tan2x + 4tanx -4=1 + tan2x
o tan X + 4tanx -5 = 0 it
tan X = 1 tan X = -5
X = — + kn 4	'
(k e Z)
 6cos2x - 6 73 sinxcosx =
0
 cosx (cosx - 73 sinx) =
0
cos X = 0
71	1
X = — + ktt
2
X = — + kĩt 2
/- ° cos X - 73 sin X = 0
r
,	• ^3
tan X = -—
3
X = — + kít. 6
Giải các phương trình
a) cosx - 73sinx= 72;
b) 3sin3x - 4cos3x = 5;
c) 2sinx + 2cosx - 72 = 0;
d) 5cos2x + 12sin2x - 13 = 0
ỐịiẢl
a) Chia hai vế phương trình cho
FW =■
2 ta được:
d)
X - arctan (-5) + kn 2cos2x - 6 73 sinxcosx - 4sin2x + 4 = 0
(k e Z)
72
— cosx 2
—— sinx = ——	cosxcos 77 - sin 77 sinx =
2	2	3	3	2
	,	, Tt ■> _ 72	7t
 COS (X + 7- ) =	= COS — 
3	2	4
n 71 , l.n. X + — = — + k2rc
n 71 l.o_ X + — =	+ k2n.
(k e Z)
3	4
71
- _ + k2rt 12
7- ,
X = - 7-7 + k2-t. 12
(k e Z)
Chia hai vế phương trình cho ^32 + (-4)2 = 5 ta được
4
— sin 3x - — cos3x = 1 sin3xcosa - sinacos3x = 1 5	5
(trong đó cosa = Ệ và sincx = 4 )
5
Ta có: sin(3x - a) = sin^ 3x - a = -^ + k27t X = 7 + -r + k^7,keZ 2	2	6	3	3
2 72 sin X + ^ = 72
. 7t = — = sin —
6
o sin Ị X +
71 _ 7t ,
X + — = 77 + k2ĩt
6
,71 5ĩt .
X + — = —- + k2n 4	6
X = --777 + k2rc
12
_ 771 , ,
X = -777 + k2z
12
(k e Z)
Ta có 2sinx + 2cosx - 72 = 0 2(sinx + cosx) = 72 7t
Chia hai vế phương trình cho Võ2 + 122 = 13 ta được 5	12
—-cos2x + — sin2x = 1 cos2xcosa + sin2xsina = 1 13	13
12
(trong đó cosa = —- và sina = —)
13	13
Ta có: cos(2x - a) = 1 2x - a = k2n X = — + kĩi, k e z 2
6. Giải các phương trình sau:
tan(2x + 1 )tan(3x - 1) = 1;
tanx + tan I X + I = 1.
ốjiài
Điều kiện cos(2x + 1) * 0, cos(3x - 1) * 0 tan(2x + l)tan(3x - 1) = 0 sin(2x + l)sin(3x - 1) = cos(2x + l)cos(3x - 1)
 cos(2x + l)cos(3x - 1) - sin(2x + l)sin(3x - 1) = 0 COS [(2x + 1) + (3x -1)] = 0 cos5x = 0
 5x = ỊỊ + krc 2
x = ^- + k^,k e z 10	5
Điều kiện cosx * 0; cos(x +
4
tanx + tan(x + y) = 1 tanx + ——	 = 1
4	1 - tan X
 tanx - tan2x + tanx +1 = 1- tanx o tan2x - 3tanx = 0
tanx(tanx - 3) = 0 o
tan X = 0 tan X = 3
X = kĩi
X = arctan 3 + kĩi
(k e Z).
c. BÀI TẬP LÀM THÊM
1. Giải các phương trình sau:
a) 6cos2x + 5sinx -7 = 0;	b) cos2x + 3sinx = 2;
c) 1 + cosx + cos2x = 0;	d) tan3x - 3tan2x - 2tanx + 4 = 0.
•’Htíớnỹ ỉẫn
Đặt t = sinx; t = —; t = — ;
3
Đặt t = cosx; t = 0; t = - — ;
2
Giải các phương trình sau:
Đặt t = sinx; t = 1; t = —
2
Đặt t = tanx; t = 1; t = 1 +V5
a)
sin2 X
+ 3tanzx + 4(tanx + cotx) -1=0;
b) 2cos:
6x
, , -	8x .
+ 1 = 3cos-^-;
c) sinBx + COS8X = ^Xcos22x.
16
•Hướng dẫn
'	9	1	71
Áp dụng công thức: 1 + cot2x =	, đặt t = tanx + cotx, X = -y + kn, k e z
sin2 X	4
Đặt t = cos^ (|t| < 1).
5
Áp dụng công thức nhân đôi và nhân ba ta được:
4t2 - 6t2 - 3t + 5 = 0 có nghiệm t = 1 sin8x + COS8X = (sin4x + cos4x)2 - 2sin4xcos4x
= 11
Đặt t = sin22x (0 < t < 1). 3. Giải các phương trình sau:
■ vsm X + cos x; - ZSU1 xcus X
fl-ịsin22xì -ịsin4 2x = 1-sin2 2x + ịsin42x <2 ) 8 8
sinx + cosx = 72 sin7x;
sinx + cosx = cos2x;
1 + sinx + cosx + sinxcosx = 0;
1 + sinx + cosx + sin2x + cos2x = 0.
•Hưởng dẫn
Áp dụng kết quả: sinx + cosx = 72 sin^x +
Áp dụng công thức nhân đôi: cos2x = COS2X - sin2x
Đưa phương trình về tích: (sinx + cosx)(l + sinx - cosx) =' 0
Đưa về tích: (1 + sinx)(l + cosx) = 0
Đưa về tích (sinx + cosx)(2cosx + 1) = 0.