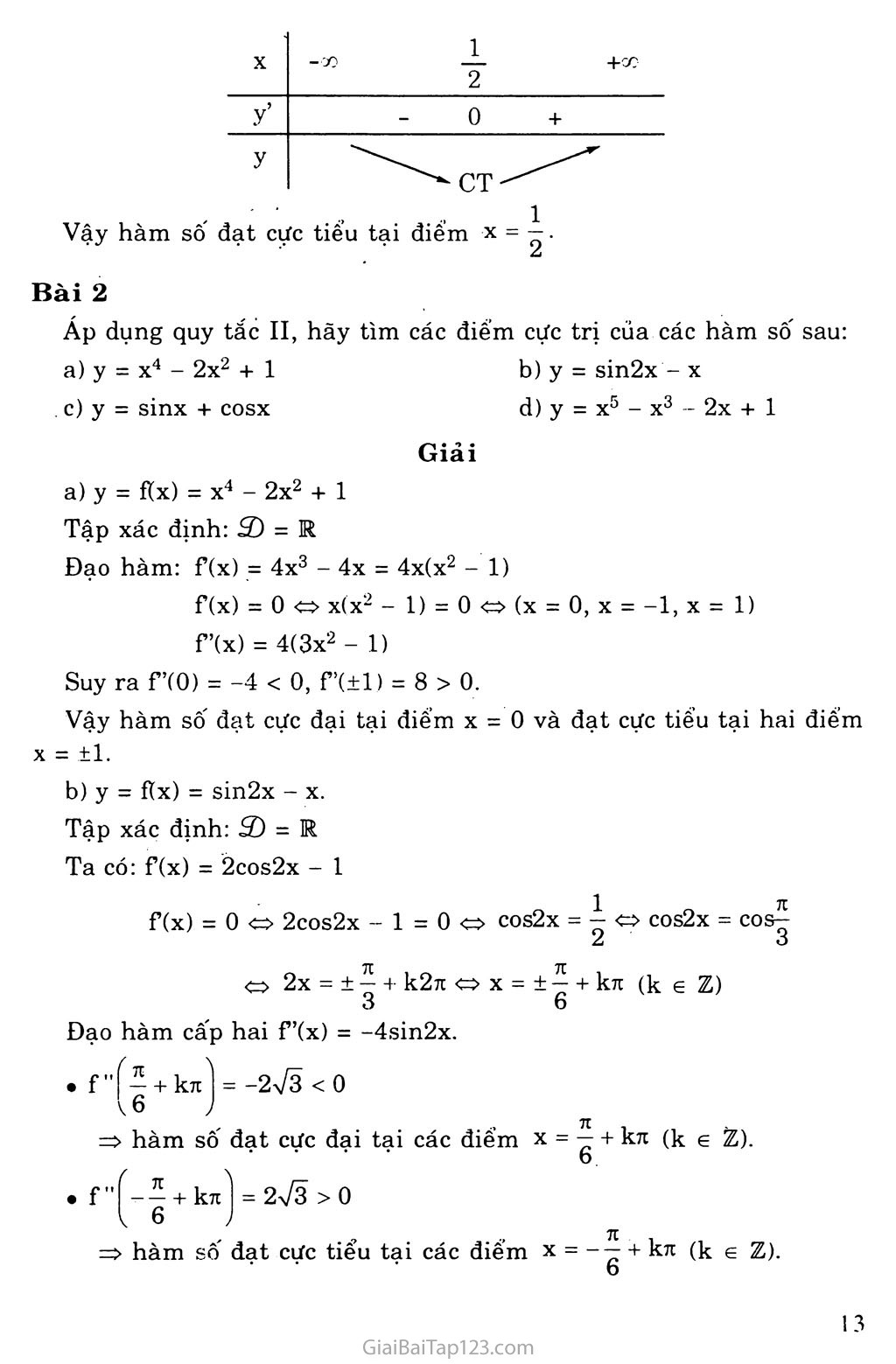Giải Toán 12: Bài 2. Cực trị của hàm số

A. KIẾN THỨC CẦN NHỚ
Định nghĩa
Cho hàm số y = f(x) xác định trên tập hợp 5)c R và x0 e S).
x0 được gọi là một điểm cực đại của hàm số f(x), nếu tồn tại một khoảng (a; b) cẩ) chứa điểm x0 sao cho:
fíx) < f(x0) với mọi X e (a; b) \ {x0Ị
Khi đó flxo) được gọi là giá trị cực đại của hàm số f(x). Ta viết yCĐ = f(x0).
x0 được gọi là mọt điểm cực tiểu của hàm số fíx), nếu tồn tại một khoảng (a; b) c ẩ) chứa điểm x0 sao cho:
fix) > f(x0) với mọi X 6 (a; b) \ íxoí
Khi đó f(x0) được gọi là giá trị cực tiểù của hàm sô f(x). Ta viết yCT = f(x0).
Các điểm cực đại và cực tiểu được gọi chung là điểm cực trị. Giá trị của hàm số tại các điểm cực trị được gọi là cực trị của hàm số. Nếu x0 là một điểm cực trị của hàm số Kx) thì ta nói hàm số đạt cực trị tại điểm x0.
Điểu kiện cần để hàm sô' đạt cực trị
Định lí 1:
Nếu hàm số y = f(x) có đạo hàm tại điếm x0 và đạt cực trị tại điểm x0 thì f(x0) = 0.
Chú ỷ:
Nếu f(x0) = 0 thì hàm số f(x) có thể không đạt cực trị tại điểm XQ.
Điểu kiện đủ để hàm sô' đạt cực trị
Định lí 2: (Dâu hiệu 1)
Cho hàm số y = f(x) có đạo hàm trên khoảng (a; b) chứa điểm x0 (có thể trừ điểm x0).
Nêu f(x) > 0 với mọi X e (a; x0) và f(x) < 0 với mọi X e (x0; b) thì hàm sô' f(x) đạt cực đại tại điểm x0.
. Nếu f(x) 0 với mọi X 6 (x0; b) thì
hàm sô f(x) đạt cực tiểu tại điểm XQ.
Định lí 3: (Dấu hiệu 2)
Cho hàm số y = f(x) có đạo hàm cấp hai trên khoảng (a; b) chứa điểm x0 sao cho f(x0) - 0 và f”(x0) * 0.
Nếu f”(x0) < 0 thì hàm số f(x) đạt cực đại tại điểm x0.
Nếu f”(x0) > 0 thì hàm số f(x) đạt cực tiểu tại điểm x0.
B. BÀI TẬP
Bài 1
Áp dụng quy tắc I, hãy tìm các điểm cực trị của các hàm số sau: ' a) y = 2x3 + 3x2 - 36x - 10	b) y = X-4 + 2x2 - 3
y = X + —	d) y = x3(l - x)2
X	
e) y = ựx2 - X + 1
Giải
a) y = 2x3 + 3x2 - 36x - 10 Tap xaù nành : S) = R
Đạo hàm: y’ = 6x2 + 6x - 36 - 6(x2 + X - 6)
y’ = 0ox2 + x- 6 = 0(x = -3 hoặc X = 2)
X
-00	■ -3
2	+CO
y’
+	0
-
0 +
y
71 -
CĐ
<-54 /
Vậy hàm số đạt cực đại tại điểm X = -3 và đạt cực tiểu tại điếm X = 2. b) y = X4 + 2x2 - 3
Tập xác định: 3) = R
Đạo hàm: y’ = 4x3 + 4x = 4x(x2 + 1)
y’ = 0 X = 0
Do X2 + 1 > 0, Vx nên y’ cùng dấu với 4x.
Vậy hàm số đạt cực tiểu tại điểm X = 0.
y = X + —
X
Tập xác định: 2) = R\{0}
Đạo hàm: y' = 1 7 =	2—
X X
y’ - 0 X2 - 1 = 0 (x = -1 hoặc X = 1)
X
-00-1	0	1	+®
y’
+ 0 -
- 0 +
ý
CĐ
^2^
CT
Vậy hàm số đạt cực đại tại diein X = -1 và đạt cực tiểu tại điềm X = 1.
y = x3(l - x)2
x = 0
3
X = —
5
X = 1
Tập xác định: 5) = R
Đạo hàm: y’ = x2(5x2 - 8x + 3) ■
y’ = 0 o x2(5x2 - 8x + 3) = 0 o
Chú ý rằng khi X / 0 thì y’ cùng dấu với 5x2 - 8x + 3.
X
—co 0
_3
5
1	+00
y’
+ 0
+ 0
- 0 +
y
^CT^^
...	.	.
Vậy hàm sô đạt cực đại tại diêm X = - và đạt cực tiêu tại diêm X = 1. 5
Nhận xét: Hàm sô có y’(0) = 0, nhưng không đạt cực trị tại điểm này, vì đạo hàm không đổi dâu.
y = ựx2 - X + 1
Tập xác định: 2) - R, vì X2 - X + 1 > 0, Vx
Đạo hàm: y ’ =	..2X ~
2vx2 - X + 1
y' = ơ2x-l = 0x = ỉ
2
Nhận thây y’ cùng dấu với 2x - 1.
■	,.x> , .	..	1
Vậy hàm sô đạt cực tiêu tại diêm X = —
Bài 2
Áp dụng quy tắc II, hãy tìm các điểm cực trị của các hàm số sau:
a) y = X4 - 2x2 4-1	b) y = sin2x - X
y = sinx 4- cosx	d) y = X5 - X3 - 2x 4- 1
Giải
y = f(x) = X4 - 2x2 4- 1
Tập xác định: 3) = R
Đạo hàm: f(x) - 4x3 - 4x = 4x(x2 - 1)
f(x) = 0 x(x2 - 1) = 0 (x = 0, X = -1, X = 1) f’(x) = 4(3x2 - 1)
Suy ra f’(0) = -4 0.
Vậy hàm số đạt cực đại tại điểm X = 0 và đạt cực tiểu tại hai điếm X = ±1.
b) y = fix) = sin2x - X. Tập xác định: 3) = R Ta có: f(x) = 2cos2x - 1
f(x) = 0 2cos2x - 1 = 0 cos2x = ỉ o cos2x = cos^
 2x = ± 4' k27i x = ± + kn (ke Z)
3	6
Đạo hàm câp hai f”(x) = -4sin2x.
• f"| ^ + k7ti = -2V3 < 0
6	71
=> hàm sô đạt cực đại tại các điểm X = -- 4- k7i (ke Z).
6
• f" -^4-kn =2^3 >0
l 6 J
=> hàm sô đạt cực tiếu tại các điếm X - - — 4- K71 (k e Z). 6
y = fix) = sinx + cosx
77 	 „ , 71
2 cos X + —
I 4
Tập xác định: 2) = R
Ta CÓ: f(x) - y2 sin X + ~ , suy ra f '(x) =
71
4
X = — + k27t
(k e Z)
4
371 .
X- —- + k.271
4
Đạo hàm cấp hai f "(x) = -5/2 sin X + y .
. z	A	X /
. f" Ị + k2n =->/2 <0
=> hàm số đạt cực đại tại các điểm X = — + k27T.
■
. f” -^ + k2n = V2 >0
( 4 J
=> hàm số đạt cực tiểu tại các điểm X = -— + k27T. 4
y = fix) = X5 - X3 - 2x + 1
Tập xác định: 3) = R
Đạo hàm: f(x) = 5x4 - 3x2 - 2 = (x - l)(x + l)(5x2 + 2)
f(x) = 0 X = ±1
Đạo hàm cấp hai: f”(x) = 20x3 - 6x = 2x(10x2 - 3)
Suy ra: f”(l) = 14 > 0 và f’(-l) = -14 < 0
Vậy hàm số đạt cực đại tại điểm X = -1 và đạt cực tiểu tại điểm X = 1.
Bài 3
Chứng minh rằng hàm số y = ựịx[ không có đạo hàm tại X = 0 nhưng vẫn đạt cực tiếu tại điểm đó.
Giải
Tập xác định: ẩ) = R
Gọi y = f(x) = ựjx|.
• Khi Ax > 0:
Ay = f(0 + Ax) - f(0) = VÃx - 0 = VÃx
Ay _ . : 1
Ax VÃx
lim = lim —~ +00
Ax->0+ Ax Ax-»o+ yAx
• Khi Ax < 0:
Ay = f(0 + Ax) - f(0) = 7-Ax - 0 = 7-Ax
Ay 1
Như vậy đạo hàm của hàm số tại điếm X = 0 không tồn tại.
Nhưng ta luôn có:
f(x) = Th > 0, Vx, và đẳng thức xảy ra khi X = 0.
Suy ra, hàm số đạt cực tiểu tại điểm X = 0.
Vậy hàm số y = T|x| không có đạo hàm tại điểm X - 0, nhưng vẫn đạt cực tiểu tại điểm đó.
Bài 4
Chứng minh rằng với mọi giá trị của tham số m, hàm số
y = X3 - mx2 - 2x + 1
luôn luôn có một điểm cực đại và một điểm cực tiểu.
Giải
Tập xác định: S) = R
Đạo hàm: y’ = 3x2 - 2mx - 2
y’ = 0 3x2 - 2mx - 2 = 0 (*)
Dễ thấy phương trình (*) có hai nghiệm số phân biệt Xp x2 (x1 < x2) và y’ đổi dấu khi X vượt qua hai nghiệm này.
Vậy với mọi m hàm số luôn có một cực đại và một cực tiểu.
Bài 5
Tìm a và b để các cực trị của hàm số
y = Ệ a2x3 + 2ax2 - 9x + b
3
K	.	. ..	5	.
đêu là những sô dương và x0 = - — là điếm cực đại. 9
Giải
Tập xác định: S) = R
Gọi y = f(x) = Ệ a2x3 + 2ax2 - 9x + b.
3
Đạo hàm: y’ = f(x) = 5a2x2 + 4ax - 9
Nếu x0 = --5
Q 9
81
• Nếu a = ~ thì f(x) =
25
V nv.- 6561
và í (x) = ———
125
Q là điếm cực đại của hàm số thì ta có:
125 , 20
—— a	-a-9 = 0
81	9
2187
——— X
125
a = Ệị hoặc a =
25
162: 2
+ —— X — 9x + b 25
2 . 324
X + ——
25 6561 2 ——— X 125
x-9
324
+ _ _ X
25
í	25
-9 = 0 x = 4“- hoặc X =
I	81
Lập bảng xét dấu, ta suy ra hàm số đạt cực đại tại điểm X = ,. 25
đạt cực tiêu tại diêm X = —.
81
5
— và
9
J25Ì
Ta có: Yct _ f I g]l
243
Do đó yCĐ và yCT đều dương khi và chỉ khi
Nếu
. _ 400	400
yCT > 0 -	+ b > 0 b > 4-4
■CT	243
a = - 4 thì f(x) = 44 X
5	5
243
18 2	_	,
—— X - 9x + b
5
Lập bảng xét dấu, ta suy ra hàm số đạt cực đại tại điểm X =
đạt cực tiểu tại điểm X = 1.
Ta có: ỹCT = f(l) = --4- + b
5
Do đó yCĐ và yCT đều dương khi và chỉ khi:
36	36
yCT > 0 - 44 + b > 0 b > 44
5	5
„ • „ 81 , ,	400 ,	„	9 x ,	36
■y 25	243	5	5
X2 + mx + 1 	 đạt cực X + m
Bài 6
Xác định giá trị của tham số m đế’ hàm số đại tại X = 2.
Giải
Tập xác định: 3) = R
Hàm số f(x) =	—	 có đạo hàm:
X + m , X2 + 2mx + m2 - 1 f (x) =	7„ 1x2	’
(x + m)
Nếu f(x) đạt cực đại tại điểm X = 2 thì ta có: m2 + 4m + 3	.
r (2) = 0 ,o .	,2	= 0 o m2 + 4m + 3 = 0, (m * -2)
(2 + m)
 (m = -1 hoặc m = -3)
Kiểm tra lại, ta chỉ nhận giá trị m = -3.
Vậy nếu m = -3 thì hàm số đạt cực đại tại điểm X = 2.