Giải Toán 12: Bài 3. Ứng dụng của tích phân trong hình học

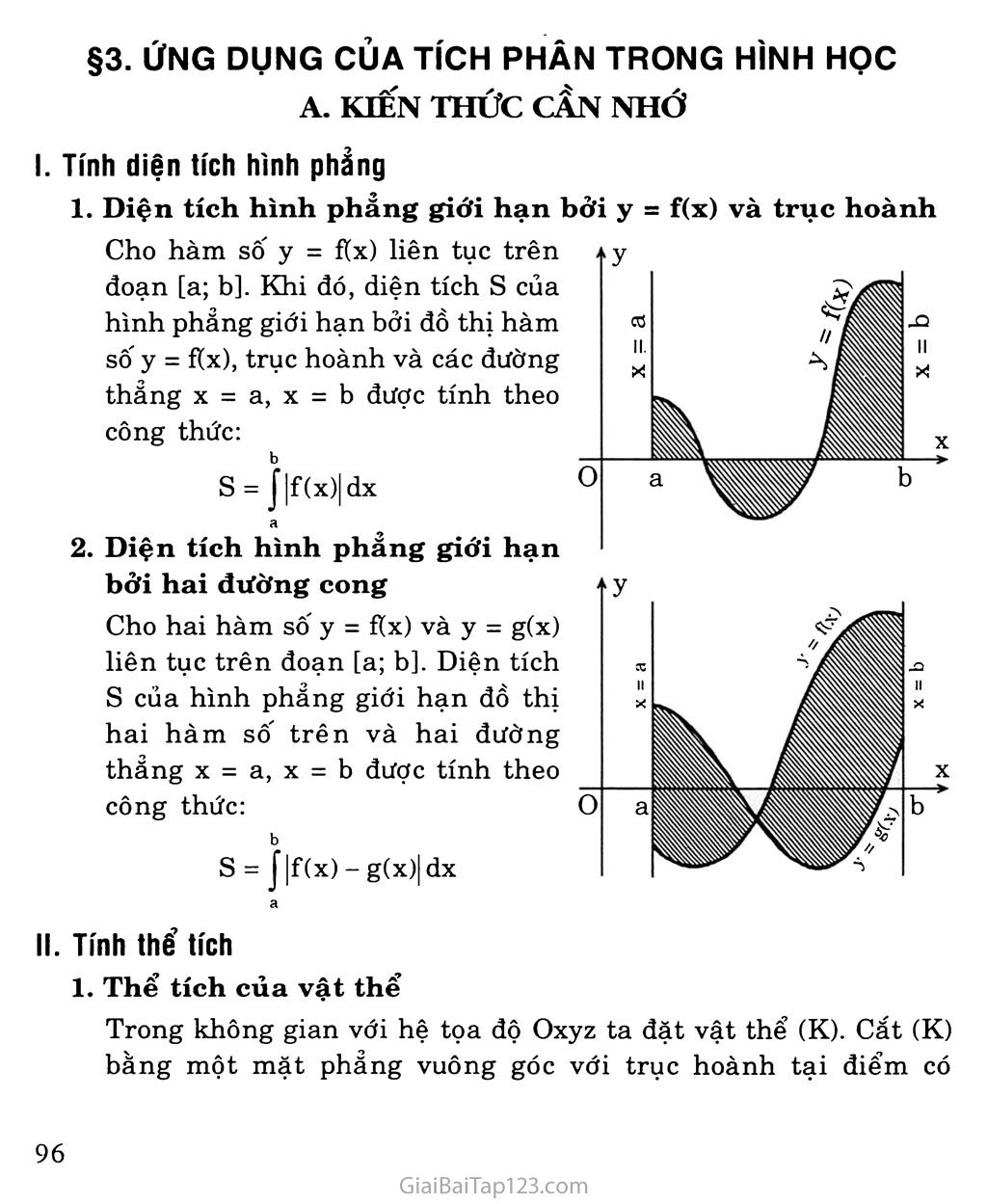
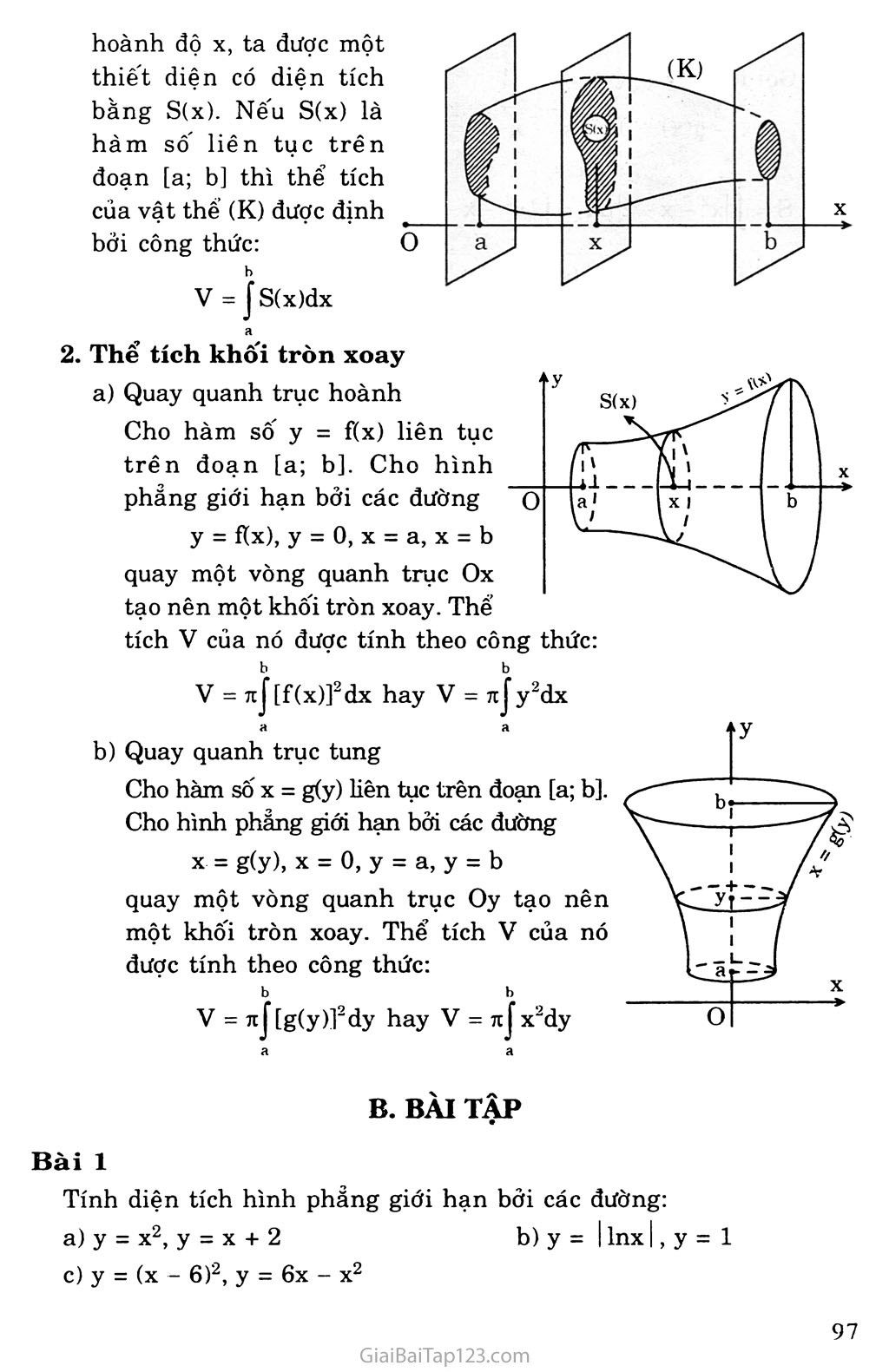
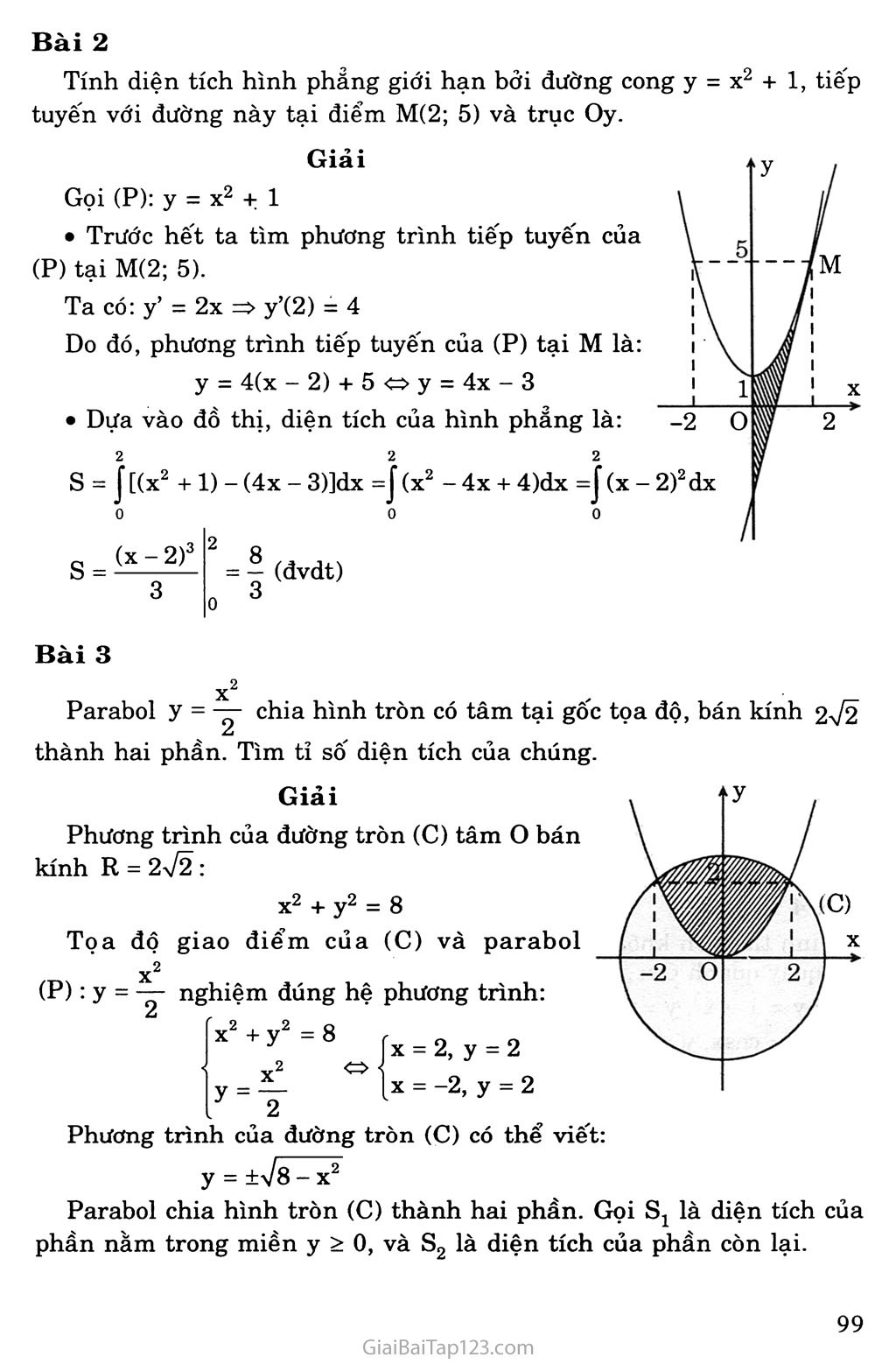
§3. ỨNG DỤNG CỦA TÍCH PHÂN TRONG HÌNH HỌC
A. KIẾN THỨC CẦN NHỚ
Tính diện tích hình phăng
Diện tích hình phẳng giới hạn bởi y = f(x) và trục hoành
Cho hàm số y = f(x) liên tục trên đoạn [a; b]. Khi đó, diện tích s của hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành và các đường thẳng X = a, X = b được tính theo công thức:
b s = J|f(x)|dx
a
Diện tích hình phẳng giới hạn bởi hai đường cong
Cho hai hàm số y = f(x) và y = g(x) liên tục trên đoạn [a; b]. Diện tích s của hình phẳng giới hạn đồ thị hai hàm số trên và hai đường thẳng x = a, X = b được tính theo công thức:
b
s = J |f(x) - g(x)| dx
II. Tính thể tích
Thể tích của vật thể
Trong không gian với hệ tọa độ Oxyz ta đặt vật thể (K). cắt (K) bằng một mặt phẳng vuông góc với trục hoành tại điểm có
hoành độ X, ta được một thiết diện có diện tích bằng S(x). Nếu S(x) là hàm sô' liên tục trên đoạn [a; b] thì thể tích của vật thể (K) được định bởi công thức:
b
V = J S(x)dx
X
Thể tích khối tròn xoay
Quay quanh trục hoành
Cho hàm số y = f(x) liên tục trên đoạn [a; b]. Cho hình phẳng giới hạn bởi các đường
y = fix), y = o,x = a, x = b quay một vòng quanh trục Ox tạo nên một khối tròn xoay. Thể
tích V của nó được tính theo công thức:
b	b
= 7t J [f(x)]2dx hay V = 7tJ y2dx
a	a
b) Quay quanh trục tung
Cho hàm số X = g(y) liên tục trên đoạn [a; b].
Cho hình phảng giới hạn bởi các đường
X = g(y), X = 0, y = a, y = b
quay một vòng quanh trục Oy tạo nên một khối tròn xoay. Thể tích V của nó được tính theo công thức:
b	b
= 71J [g(y)]2dy hay V = 71J x2dy
a	a
B. BÀI TẬP
Bài 1
Tính diện tích hình phẳng giới hạn bởi các đường:
y = X2, y = X + 2	b) y = I Inx I, y = 1
y = (x - 6)2, y = 6x - X2
Giải
a) Gọi f(x) = X2, g(x) = X + 2
f(x) - g(x) = 0ox2-x-2 = 0
2
fix2 -X
2
í (x2 - X - 2)dx =
X = —1
X = 2
X3
^-2x
3	2
-1
9
= (đvdt)
2
b) Gọi fíx) = I Inx I, g(x) = 1
X = e
1
X = —
e
Ta có s = J(1 - |lnx|)dx =J(1 + lnx)dx + J(1 - lnx)dx
111
Tính JInxdx.
Đặt u = Inx, dv = dx, ta được du = — dx, V = X X
Do đó J Inxdx = X Inx - I dx = X Inx - X + c
1
r	1
J (1 + lnx)dx = (x + X Inx - x) I = —
1	— e
e
J (1 - ln x)dx = (x - xln X + x)
e
= e-2
1
Vậy: s = — + e - 2 (đvdt)
c) Gọi f(x) = (x - 6)2, g(x) - 6x - X2
f(x) - g(x) = (x - 6)2 - (6x - X2) = 2x2 - 18x + 36
f(x) - g(x) = 0 2x2 - 18x + 36 = 0 (x = 3 hoặc X = 6)
Do đó:
- 18x + 36)dx
6
3
c 2x3
—— 9x2 + 36x
l 3	>
Vậy s = 9 (đvdt).
= ị-9| = 9
Tính diện tích hình phảng giới hạn bởi đường cong y = X2 + 1, tiếp tuyến với đường này tại điểm M(2; 5) và trục Oy.
y /
V 5
i\ l\
1 \
■
/1
/1
1 \
1	\
! 1
1
f 1 ĩ
-2 0
I 2'
2)2dx
/
Giải
Gọi (P): y = X2 + 1
Trước hết ta tìm phương trình tiếp tuyến của (P) tại M(2; 5).
Ta có: y’ = 2x => y’(2) = 4
Do đó, phương trình tiếp tuyến của (P) tại M là: y = 4(x -2) + 5y = 4x-3
Dựa vào đồ thị, diện tích của hình phẳng là:
2
+ 1) - (4x - 3)]dx =J (x2 - 4x + 4)dx =J (x -
0	0
2
s = ị[(x’
s=(x_2)l
3
Q
= ? (đvdt)
3
0
Bài 3
X2 , . , ' ,
Parabol y = — chia hình tròn có tâm tại gốc tọa độ, bán kính 2V2 thành hai phần. Tìm tỉ số diện tích của chúng.
Giải
X2 + y2 = 8
Phương trình của đường tròn (C) tâm o bán kính R = 2V2 :
X2
(P):y4
Tọa độ giao điểm của (C) và parabol nghiệm đúng hệ phương trình:
X = 2, y = 2
X = -2, y = 2
|x2+y2=8
• X2
Phương trình của đường tròn (C) có thể viết:
[y 2 y = ±yjs-x2
Parabol chia hình tròn (C) thành hai phần. Gọi là diện tích của phần nằm trong miền y > 0, và S2 là diện tích của phần còn lại.
Vì Oy là trục đối xứng của (C) và (P) nên ta có:
2
Sj = 2 J \/8 - x2 - dx =
0 \	2 ,
X3
2_ 8
0 3
0
2
• Tính J ^8-x2ảx
0
Bặt X = 2V2 sint, te “
2 ’ 2 Suyra
dx = 2V2 cost.dt
2 í
Khi X = 0 thì t = 0, khi X = 2 thì t = —.
4
7t	7t	Tt
2 	 4 	 4	4
0
= 4 -7 + 9 = 7T + 2 14 2)
0
7t
4
Do đó J78-x2dx = Iự8(l-sin2t).2V2cost.dt = 8jcos2t.dt = 4j(l + cos2t)dt 00
. f,	sin2t
= 4 t + —7-—
l 2
Suy ra Sj = 2(71 + 2) -
o O
Diện tích của phần còn lại:
S2 . k(272)2 -	- 8k - ỉĩií = 18v4
3	3	3
Vậy tỉ số diện tích của hai phần theo đề bài là:
Sj 9n - 2
k = —L = —-—-
S2 3n + 2
Bài 4
Tính thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường sau quay quanh Ox:
y = 1 - X2, y = 0
y = cosx, y = 0, x = 0, X = JX
y = tanx, y = 0, X = 0, x = 4
Giải
a) Phương trình hoành độ giao điểm của đồ thị hàm sô' và trục hoành:
1	1	/5	3	\ 1	lf>
Do đó: v = TrRl-x^dx = 7ii(x4-2x2+l)2dx-7t-2^-+ x =-— (đvtt)
-1	i	15	3	J _4	15
b)
c)
\ 7t
) 0
71
4 =
0
sin2x
X + —-—
2
TT f 2	, X -
0	“	0
4	4
V = TiJ tan2xdx = nJ ((1 + tan2x) - l)dx = 7i(tanx - x)
0	0
V = 7Ĩ f cos2xdx = f (1 4- cos2x)dx =
J 2 J	2
= (dvtt)
2
71 l--y (đvtt)
I 4 J
Bài 5
Cho tam giác vuông OPM có cạnh OP nằm trên trục Ox.
Đặt POM = a,OM = R |oO| , ,7 I 3 _ )
Gọi V là khối tròn xoay thu được khi quay tam giác đó xung quanh trục Ox.
Tính thế tích của V theo a và R.
Tìm a sao cho thể tích của V lớn nhất.
Giải
Phương trình của đường thẳng OM là: y = xtana
Hoành độ của điểm M là: a = XM = Rcosa
Thể tích của V:
a	a	.	2	a _ J	2 _
V = 71 f (xtana)2dx = 7itan2af x2dx = 71 an a .X3 = - an a.R3 cos3a
V = — TtR3 sin2a cosa = 4 7iR3(cosa - cos3a), 3 J	3
b) Tim a để V lớn nhất: Gọi f(x) = X - X3 với X - cosa Do 0 < a < nên ị
3	2
Jo	Ỉ	3	0	3
1
X = —7=
Ta CÓ f(x) = 1 - 3x2, f'(x) = 0
73
1
X =	7=
73 f"(x) = -6x=>f”|-k] = -2I/3 <0
..	. 17777.. 1
27
Suy ra fix) đạt cực đại tại điếm X =	, khi đó maxV =
Vậy maxV = ^3. KR3 khi cos a =	.