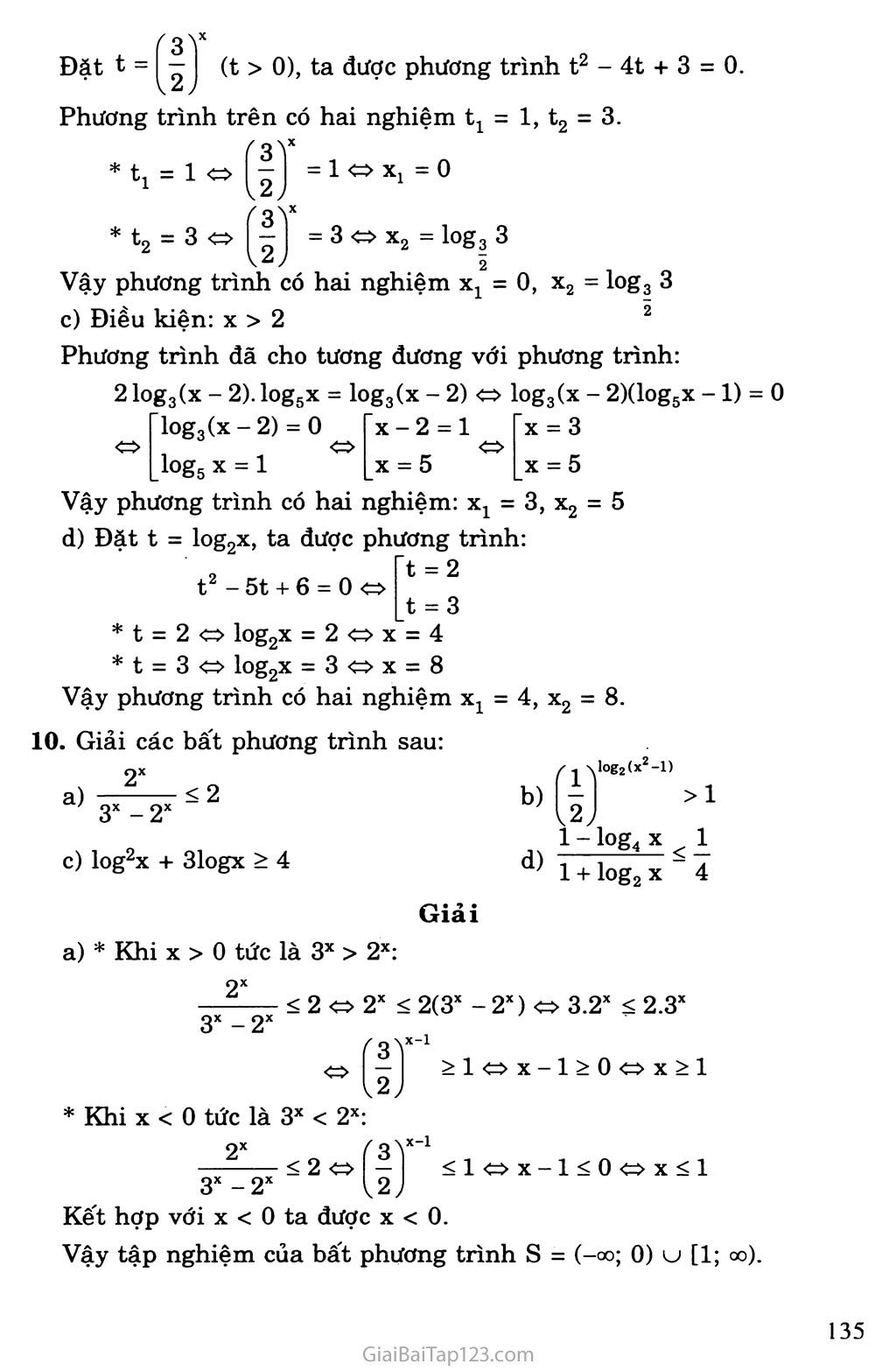Giải Toán 12: Ôn tập cuối năm

ÔN TẬP CUỐI NĂM
Các câu hỏi từ 1 đến 10, độc giả xem lại trong sách giáo khoa.
I. Câu hỏi
1. Định nghĩa sự đơn điệu (đồng biến, nghịch biến) của một hàm số trên một khoảng.
Phát biểu các điều kiện cần và đủ đế hàm số f(x) đơn điệu trên một khoảng.
Phát biểu các điều kiện đủ đế’ hàm số f(x) có cực trị (cực đại, cực tiểu) tại điểm XQ.
Nêu sơ đồ khảo sát sự biến thiên và vẽ đồ thị của hàm số.
Nêu định nghĩa và các tính chất cơ bản của lôgarit.
Phát biểu các định lí về quy tắc tính lôgarit, công thức đổi cơ số của lôgarit
Nêu tính chất của hàm số mũ, hàm số lôgarit, mối liên hệ giữa đồ thị các hàm số mũ và hàm số lôgarit cùng cơ sô'.
Nêu định nghĩa và các phương pháp tính nguyên hàm.
Nêu định nghĩa và các phương pháp tính tích phân.
Nhắc lại các định nghĩa số phức, số phức liên hợp, môđun của số phức. Biểu diễn hình học của số phức.
Bài tập
1. Cho hàm số fix) = ax2 - 2(a + l)x + a + 2 (a 0)
Chứng tỏ rằng phương trình f(x) = 0 luôn có nghiệm thực. Tính các nghiệm đó.
Tính tổng s và tích p của các nghiệm của phương trình f(x) = 0. Khảo sát sự biến thiên và vẽ đồ thị của s và p theo a.
Giải
2
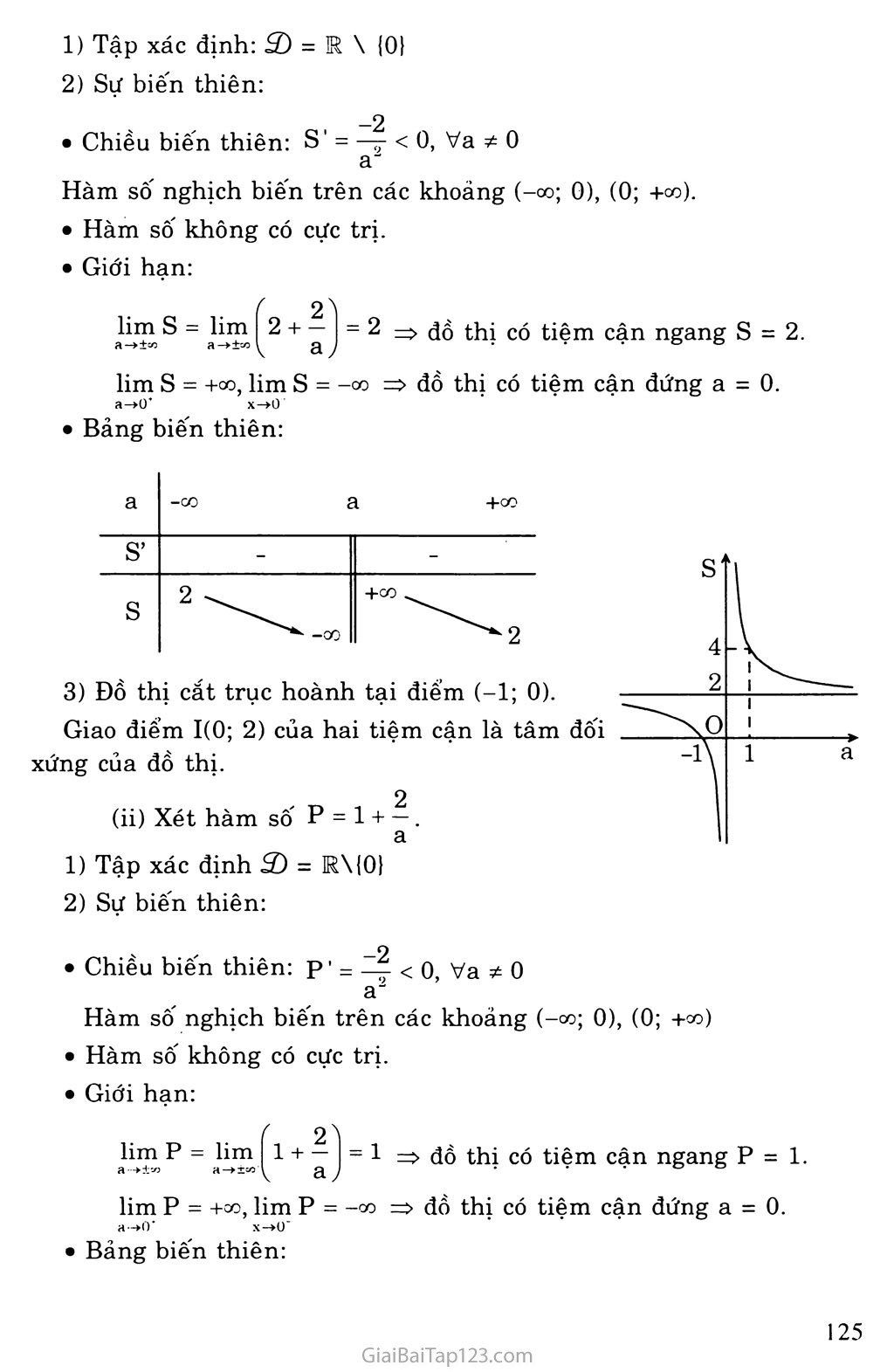
(i) Xét hàm sô' s = 2 + —
a
Tập xác định: S) - R \ ỊOÍ
Sự biến thiên:
• Chiều biến thiên: S' - —y < 0, Va 0 a
Hàm số nghịch biến trên các khoảng (-co; 0), (0; +co).
Hàm số không có cực trị.
Giới hạn:
lim s - lim 2 + — - 2 đồ thị có tiệm cận ngang s = 2. a—>±co	a—>±co I	a, y	■
lim s = +00, lim s = -co => đồ thị có tiệm cận đứng a = 0. a->0+	x-*0”
• Bảng biến thiên:
S’
a
-co	a
+co
P’
-
p
1
-co
+co
"^1
Đồ thị cắt trục hoành tại điểm (-2; 0).
Giao điểm J(0; 1) của hai tiệm cận là tâm đối xứng của đồ thị.
Cho hàm số y = - — X3 + (a - l)x2 + (a + 3)x - 4.
O
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm sô khi a = 0.
Tính diện tích hình phẳng giới hạn bởi (C) và các đường thẳng y = 0, X = -1, X = 1.
Giải
1	3	2
Khi a = 0 phương trình của hàm sô trở thành y = - — X' - X + 3x - 4.
Tập xác định: 3) - R
Sự biến thiên:
Chiều biến thiên: y’ - -X2 - 2x + 3, y’ = 0 X = -3 hoặc X = 1 Suy ra:
y’ < 0 khi X e (-co; -3) u (1; +co). Hàm số nghịch biến trên các khoảng (-co; -3), (1; +co).
y’ > 0 khi X e (-3; 1). Hàm số đồng biến trên khoảng (-3; 1).
Cực trị: Hàm số đạt cực tiêu tại điểm X = -3, yCT = -13 và đạt cực đại tại điểm X = 1, yCĐ = - —
O
Các giới hạn: lim y = lim X
= +co
lim y = lim X
X—>——30
1 A
3 X X2 X3
1 _ 1 3 _±
3 XX2 X3
Bảng biến thiên:
X
-CO
-3
1
+co
y’
0
+ 0
-
y
-4-00
^-13"
-
3
—cc-
Cho hàm số y = X3 + ax2 + bx + 1.
Tìm a và b đê đồ thị của hàm số đi qua hai điểm A(l; 2) và B(-2; -1).
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số ứng với các giá trị tìm được của a và b.
Tính thể tích vật thể tròn xoay thu được khi quay hình phẳng giới hạn bởi các đường y = 0, X - 0, X - 1 và đồ thị (C) xung quanh trục hoành.
Giải
a) Đồ thị hàm số đi qua hai điểm A(l; 2) và (-2; -1) khi và chi khi:
|T + a + b + 1 = 2	[a + b = o	ịa = l
[-8 + 4a - 2b + 1 = 1	[2a - b = 3	[b = -1
b) Khi a = 1 và b = -1 phương trình của hàm sô trở thành:
y = x3 + x2-x + l
Tập xác định: 3) - R
Sự biến thiên:
• Chiều biến thiên: y' = 3x2 + 2x - 1, y' - 0 X - -1 hoặc X - —
. Hàm sô’ đồng biên trên các
0 khi X e (-co; -1) o I —; +CO
13
khoảng (_00ỉ~
. Hàm sô’ nghịch biến trên khoảng
y' < 0 khi X e
• Cực trị: Hàm sô’ đạt cực đại tại điếm X = -1, yCĐ = 2 và đạt cực
22
tiểu tại điếm X = yCT =	.
0	ỉ
Các giới hạn:
và lim y = lim X3
-1
22
27
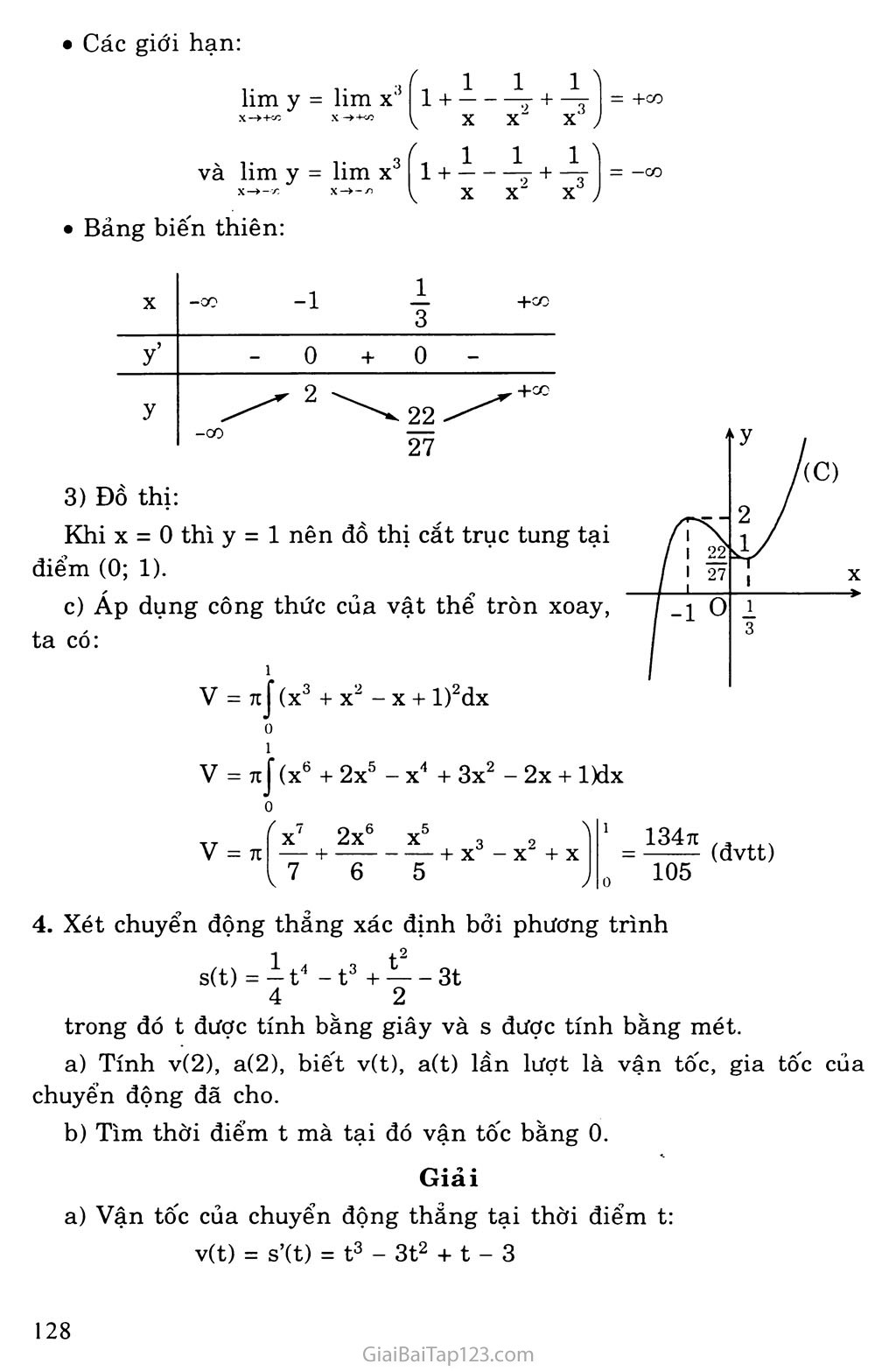
+ X2 - X + l)2dx
J(x6
0
fx7
+ 2x5 - X4 + 3x2 - 2x + l)dx
2x6 X5 3	2
„	_ + X - X
7	6	5
(đvtt)
1 _ 134 7t o“ 105
■y
/(C)
2 .
/1 \
/ 1 22
1/
/ 1 27
/	1
1
X
/ 0
_Ị_
3
3) Đồ thị:
Khi X = 0 thì y = 1 nên đồ thị cắt trục tung tại điểm (0; 1).
c) Áp đụng công thức của vật thể tròn xoay, ta có:
-00
Bảng biến thiên:
lim y = lim X3
Gia tốc của chuyển động thẳng tại thời điểm t:
a(t) = v’(t) = 3t2 - 6t + 1
Suy ra: v(2) = -5 (m/s), a(2) = 1 (m/s2)
Theo giả thiết ta có phương trình:
v(t) = 0 t3 - 3t2 + t - 3 = 0 (t - 3)(t2 + l) = 0t = 3 Vậy khi t = 3 thì vận tốc bằng 0.
Cho hàm số y = X4 + ax2 + b.
Tính a, ■; để hàm số có cực trị bằng 2 khi X = 1.
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho khi
a = b = 1.
Viết phương trình tiếp tuyến của (C) tại các điểm có tung độ bằng 1.
Giải
Gọi Kx) = X4 + ax2 + b, suy ra f(x) = 4x3 + 2ax.
Từ giả thiết ta có hệ phương trình:
f'(l) = o	Í4 + 2a = 0	[a = -2
f(l) = <	l + a + b=37	b =-T
l 2 l 2 l 2
5
Vậy a = -2 và b = .
1
Khảo sát hàm số y = X4 - — X2 +1 (ứng với a = - — và b = 1)
Tập xác định: S) = R
Sự biến thiên:
• Chiều biến thiên: y’ = 4x3 - X = x(4x2 - 1)
y' = 0 x(4x2 -1) = 0 
X = 0 hoặc X = ±4
2
y' < 0 khi X G
1
—co;	
2
uí0;ỉì-
l 2 '
Hàm số nghịch biến trên các khoảng
J.
2
. Hàm số đồng biến trên các khoảng
y ' > 0 khi X e
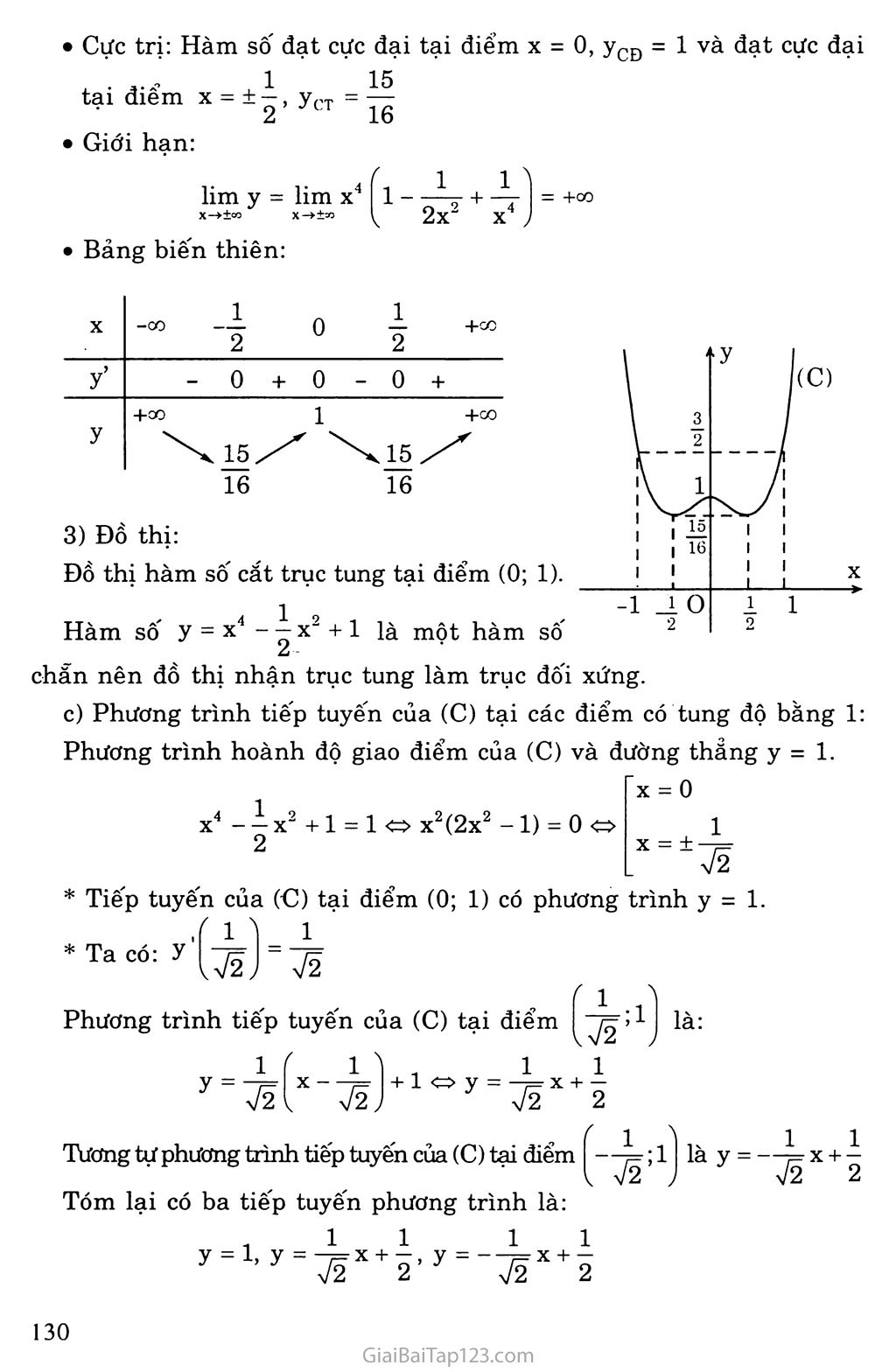
Cực trị: Hàm số đạt cực đại tại điểm X = 0, yCĐ = 1 và đạt cực đại
, 1	15
tại diêm X = + —, yPT = —
2 CT 16
Giới hạn:
lim y = lim X4 1 - ~~ + —7- = +co X->±00	X->±so	I 2x2 X4;
• Bảng biến thiên:
chẵn nên đồ thị nhận trục tung làm trục đôi xứng.
Phương trình tiếp tuyến của (C) tại các điểm có tung độ bằng 1:
Phương trình hoành độ giao điểm của (C) và đường thẳng y = 1.
X = 0
X4-ịx2+1 = 1 o x2(2x2-1) = 0 «	1
2	X = ±-7=
72
Tiếp tuyến của (C) tại điểm (0; 1) có phương trình y = 1.
1 ì 1
Ta có:	=
	, _ , . f 1 J
Phương trình tiếp tuyến của (C) tại điểm I J2’1 I là: lí 1 ì . ~	1 .. . 1
V2I	72;	72	2
Tương tự phương trình tiếp tuyến của (C) tại điểm —; 1 \ V 2
Tóm lại có ba tiếp tuyến phương trình là:
. 1.1	1 .. . 1
y = 1, y = -7= X + —, y = —7= X + — 72	2	72	2
Cho hàm số y =	—— .
X + m - 1
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số khi m = 2.
Viết phương trình tiếp tuyến d của đồ thị (C) tại điểm M có hoành độ a -1.
Giải
, , '	X - 2
Khi m = 2 phương trình của hàm sô trở thành y = ——.
X +1
Tập xác định: S) = R\{-1}
Sự biến thiên:
3
Chiều biến thiên: y' = -———7T > 0, Vx * -1
(x + lr
Hàm số đồng biến trên các khoảng (-co; -1), (-1; +oo)
Hàm số không có cực trị.
Giới hạn:
1--
lim y = lim	Y - 1 => đồ thị có tiệm cận ngang y = 1.
X—>±CQ	X—>±cc	1
1 + -
X
lim y = -00, lim y = +C0 => đồ thị có tiệm cận đứng X = -1. x-»(-ir	x->(-ir
Bảng biến thiên:
Đồ thị cắt trục tung tại điểm (0; -2), cắt trục hoành tại điểm (2; 0).
Giao điểm K-l; 1) của hai tiệm cận là tâm đối xứng của đồ thị.
Phương trình của tiếp tuyến d:
Lấy điểm M bất kì trên (C) với XM = a (a -1)
y'(a) =
—3	
(a + l)2
a - 2
XM = a yM = Ỹ và
a +1
Phương trình tiếp tuyến của (C) tại M là:
, a - 2	3	.. . à' - 4a - 2
y - 7	—7 (x - a) +	- y = -	— X + — 	7-5—
(a + 1)2	a + 1 (a + 1)2 (a + 1)2
_ “	_	2
Cho hàm sô y = —— .
2 - X
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm sô' đã cho.
Tìm các giao điểm của (C) và đồ thị của hàm số y = X2 + 1. Viết phương trình tiếp tuyến của (C) tại mỗi giao điểm.
Tính thể tích vật thể tròn xoay thu được khi quay hình phẳng H giới hạn bởi đồ thị (C) và các đường thẳng y = 0, x = 0, X=1 xung quanh trục Ox.
Giải
a) Khảo sát hàm số y = —-—.
2 - X
Tập xác định: S) = ]R\(2Ị
Sự biến thiên:
Chiều biến thiên: y ’ =
> 0, Vx 2
2
(2 - X)2
X -co
2
Hàm số đồng biến trên các khoảng (-co; 2), (2; +co)
• Hàm số không có cực trị.
Giới hạn:
2	,
lim y = lim —=— = 0 => đồ thị có tiệm cận ngang y = 0. x->±»	x->±«.2 — X	•	b
lim y = -00, lim y = +co => đồ thị có tiệm cận đứng X = 2. x->2*	x-»2'
Bảng biến thiên:
Đồ thị cắt trục tung tại điếm (0; 1).
Giao điểm 1(2; 0) của hai tiệm cận là tâm đôi xứng của đồ thị.
Gọi (P): y = X2 + 1
Phương trình hoành độ giao điểm của (C) và (P):
——— = X2 + 1 x(x - l)2 = 0 o
2 - X
Suy ra (C) và (P) có hai giao điểm là A(0; 1) và B(l; 2).
Ta có: y '(0) = - và y ’(1) = 2
Zu
Phương trình tiếp tuyến của (C) tại A:
„ 1 , ,
y = —X + 1
2
Phương trình tiếp tuyến của (C) tại B:
y = 2(x - 1) + 2 y = 2x
Áp dụng công thức thể tích của vật thể tròn xoay, ta có:
1
-- 2n (đvtt)
ỵ X	-.2	1
V = 71 í I —-— I dx = 4tt í -—--- „ dx = -4tc —-i— 0<2-xJ J (x - 2)2	x-2
8. Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hẳm số:
-41
2j
trên đoạn [1; e]
trên nửa khoảng [0; +co)
L.3 ' trên đoạn U’2n
a) fix) = 2x3 - 3x2 - 12x 4- 1 trên đoạn
fix) = x2lnx
f(x) = xe~x
d) f(x) = 2sinx + sin2x
Giải
f(x) = 6x2 - 6x - 12 = 6(x2 - X - 2)
	„ „(5
Ta có: fl-l) = 8, fl2) = -19, fl-2) = -3, f I I
r „ 5Ì
X ex. V4 1 U-l LUCl	vx cu	—ĩ 2
f(x) = 0x2-x-2 = 0x = -l hoặc X = 2 33
2
Suy ra: - GTLN của fix) trên “2; 2 là fl-l) = 8 '	.51
- GTNN của f(x) trên “2;^ là f(2) = -19
f(x) = x(21nx + 1), (x > 0)
f(x) = 0 x(21nx + 1) = 0 X = Ế [l;e] e
Suy ra: - GTLN của fix) trên [1; e] là fle) = e2
- GTNN của fix) trên [1; e] là fll) = 0
f(x) = (1 - x)e x, f(x) = 0 X = 1
Từ bảng ta suy ra max f(x) = f(l) = —
[Oi-Ho)	e
Vì fix) = xe~x > 0, Vx e [0; +co) nên min f(x) = f(0) = 0
(0;+=o)
d) f(x) = 2cosx + 2cos2x = 2(cosx + cos2x)
f(x) - 0 cosx + cos2x = 0 o cos2x = cos(7i + x) X = 71 + k27T
«	7t . 2tc
X = --T- + k—-
L 3	3
n. 3tt
xe 0 —-
2
(k e Z)
suy ra
71
X = 71, X = —
3
c 71
Ta co: f(7L) = 0, f I—
3^3
2
-2
X
-00	1	+C0
f(x)
+	0
fix)
1
=ì = -2
2 )
Vậy trên đoạn 0;ậ f(x) có GTLN = fí?ì = ^ và GTNN = f
2	13 J 2
9. Giải các phương trình sau:
132x+1 - 13x - 12 = 0
(3X + 2X)(3X + 3.2X) = 8.6X
log^(x-2).log5 X = 2.1og3(x-2)
logs X - 5 log2 X + 6 = 0
Giải
132x+1 - 13x - 12 = 0 o 13,(13x)2 - 13x - 12 = 0
Đặt t = 13x (t > 0), ta được phương trình 13t2 - t - 12 = 0.
12
Phương trình trên có hai nghiệm tx = 1, t2 (loại M Ta được: tj = 13 13x = 1 X = 0
Vậy phương trình có một nghiệm X = 0.
(3X + 2X)(3X + 3.2X) = 8.6X	(3X)2 - 4.3X.2X + 3(2X)2 = 0
V
-4
Í 3Y
Đặt t = 9 (t > 0), ta được phương trình t2 - 4t + 3 = 0.
Phương trình trên có hai nghiệm t1 = 1, t2 = 3.
tx = 1 IJJ = 1 cx> Xx = 0
<3V
t2 = 3 « I = 3 x2 = logạ 3
' z -	.	- .	2
Vậy phương trình có hai nghiệm xx = 0, x2 = log3 3
Điều kiện: x > 2	2
Phương trình đã cho tương đương với phương trình:
2 log3(x - 2). log5x = log3(x - 2) log3(x - 2)(log5x - 1) = 0
log3(x - 2) = 0
log5 X = 1
X - 2 = 1 X = 3
X = 5 X = 5
Vậy phương trình có hai nghiệm: xx = 3, x2 = 5
Đặt t = log2x, ta được phương trình:
* t = 2 log2x = 2 X = 4
t2 - 5t + 6 = 0 «
= 4, x2 = 8.
* t = 3 o log2x = 3 X = 8 Vậy phương trình có hai nghiệm xx
10. Giải các bất phương trình sau:
2X
a) —- -v <2
3X - 2
log2x + 31ogx > 4

Z. xlog2(x2-l)
b> IJ j
ì- log4 X	1
' 1 + log2 X	4
Giải
a) * Khi X > 0 tức là 3X > 2X:
2X
— 2X < 2(3X - 2X) « 3.2X < 2.3X
3X - 2
/ o \ x 1
o ị >l»x-l>0ox>l
<2j
* Khi X < 0 tức là 3X < 2X:
9X	í Q
- < 2 « I <1^X-1<O«X<1
3-2	<2J
Kết hợp với X < 0 ta được X < 0.
Vậy tập nghiệm của bất phương trình s = (-oo; 0) u [1; oo).
Điều kiện X +1 ị_t > 1
XT- 1 - loỗ2 X _ _ rloể2 X < -1
 Như vậy: 7—;	
 1 + log2 X |_log2 X > 1
 Kết hợp với điều kiện ta được tập nghiêm của bất phương trình là:
 = ^0;|ju[2;+oo)
 11. Tính các tích phân sau bằng phương pháp tích phân từng phần:
 - 1 > 0 o (x 1)
Với điều kiện đó ta có:
/	\ log2(x2-!)
—	> 1 log2(x2 -1) X2 -1 X2 < 2
 -72 < X < V2
Kết hợp với điều kiện ta được tập nghiệm của bất phương trình là: s = (-72;-1) o (1; 72)
Điều kiện X > 0
Ta có: log2x + 31ogx > 4 log2x + 31ogx - 4 > 0
t2 + 3t - 4 > 0 
t <-4
t > 1
logx < -4
logx > 1
Vậy tập nghiệm của bất phương trình là:
o[10; +00)
. 1
Như vậy: log2x + 3 logx - 4 > 0 
S = |0;—
10000
c) Điều kiện X > 0 và
X * 7-
2
0<x<	1
10000
X >10
Đặt t = logx, bất phương trình trên trở thành bất phương trình:
Ta có: Ị - ‘°g< x < - <7, 2'0g2 x s - o 1 ~ !°Ea x s 0 (*)
1 + log2 X 4	1 + log2 X 4	1 + log2 X
Đặt t = log2x, bất phương trình (*) trở thành:
r xdx b) J sin2 X
7x ln xdx
7t
J (rt - x) sinxdx
0
6
0
J (2x + 3)e"xdx
-1
Giải
dx	2 ị
a) Đặt u = Inx và dv = Vxdx> ta được du = — và V = X2 X	3
8 6	4 i~3
3	9
9 r -
- 77 [ x2dx =
31
= |etì -ị(e6-l) = |(5e6+1) 3	9	9
fix
b) Đặt u = X và dv =	—
sin X
, ta được du = dx và V = -cotx
7t
" f cosx . 7TV3 . , .	.
+	; dx = —T— 4- In(sinx)
ị sinx 6
6
í x<^r dx = -X cotx
J sin X
6
Đặt u = 71 - X và dv = sinxdx, ta được du = -dx và V =
71
J (n - x) sinxdx = (x - Ti) cosx
7t Ị
- I cosxdx = 71 - sinx
0	0
7W3	,
—+ ln2
6
-cosx
7t
= 71
0
Đặt u = 2x + 3 và dv = e“xdx, ta được du = 2dx và V =
0 I (2x + 3)e’xdx = -(2x + 3)e
12. Tính các tích phân sau bằng phương pháp đổi biến số:
n
24	/	\	\
a)
b)
0 v	'
3
í —dx.- 9 (dặt X = tan t)
J 9 + 25x2	5
5
	71	,
u = cos — - 4x
3
c)
d)
2
Jsin3 xcos4 xdx (đặt u = cosx)
0
n
r Jl + tanx ,	r— 	x
1 -	dx (đặt u = ^/1 + tanx)
\ COS2X
4
Giải
24
ả sin
a)
dx
° cos
-e_x
0
= 3e-5
—. „ ,	I 71	I	,	1.(71	I ,
Đăt u = cos — -4x => du = — sin — -4x dx •	I o	I 4	<3
...	71	.
71
<3	)
Khi X. = 0 thì u = ị,
2
24
khi X = thì u = —p-
2
Tặ
2
= ịln3
8
3
b) Ta có: J d* 2 Vã 9 + 25x
5
3	(
Đặt X = — tan t,t e
5	1
./3
Khi x = thì
2 3
5
~ + X2
5 25
-71 . 71^
T’iJ’
t = và khi X = Ệ thì t = — 6.5
7Ĩ
dx 1 11 + tan21
JL 9 + 25x2 - 15 J 1 + tan21
~5	6
c) Đặt u = cosx => du = -sinxdx
3	9
suy ra dx = -^ (1 + tan2 t)dt
5
71
4’
71
6
n
180
7L - x
Khi X = 0 thì u = 1 và khi X = -r thì u = 0
ir	ir
2	2
J sin3 X cos4 xdx =J (1 - cos2 x) cos4 X sin xdx
0	0
1
= J (1 - u2)u4du =
0
d) Đặt u = ựl + tan X
<„5
,7 \
u
u
0
I2 = 1 + tanx => 2udu =
2
35
—dx
cos X
Khi X = - 4 thì u = 0 và khi X = — thì u = V2
4	4
Tã	„
Ĩ u2du =^U3
Jo	3
I ựl + tanx
cos2x
~ĩ
13. Tính diện tích hình phẳng giới hạn bởi các đường:
y = X2 + 1, X = -1, X = 2 và trục hoành.
y = Inx, X = — X = e và trục hoành.
J	e	•
'2
'2
4V2
3
Giải
2
Ta có s = J (x2 + l)dx =
Dễ thấy đồ thị hàm số
= 6 (đvtt)
-1
y = Inx cắt trục hoành tại điểm (1; 0).
e	1	e
Do đó: s = I|lnx| dx = -JIn xdx +|In xdx
1	1	1
(- ,e Tính J In xdx.
Đặt u = Inx và dx = du, ta được du = — và V = X.
J In xdx = xlnx-jdx = xlnx-x + c
Vậy:
s = -(xlnx - x)
1
e
+ (xlnx - x)
1
1
e
9 A	2
1 - — +1=2-— (đvtt) e)	e
14. Tìm thể tích vật thể tròn xoay thu được khi quay hình phẳng giới
hạn bởi các đường y = 2x2 và y = X3 xung quanh trục Ox.
Giải
Gọi fix) = 2x2 và g(x) = X3.
f(x) - g(x) = 2x2 - X3 = x2(2 - x)
f(x) - g(x) = 0 x2(2 - x) = 0 
Thể tích của vật thể tròn xoay sinh ra là:
2	2	2	2
V = mJ*(2x2)2dx - nJ(x3)2dx = 4nJx4dx - 71Jx6dx
0	0	0	0
2 25671
35
4n 5
= ^7~x5
5
Giải các phương trình sau trên tập số phức:
(3 + 2i)z - (4 + 7i) = 2 - 5i b) (7 - 3i)z + (2 + 3i) = (5 - 4i)z
z2 - 2z + 13 = 0	d) z4 - z2 - 6 = 0
Giải
6 + 21
a) (3 + 2i)z - (4 + 7i) = 2 - 5i (3 + 2i)z = 6 + 2i o z = ^^7
3 + 21
(6 + 2i)(3 - 2i)	22	6 ;
o z = 	77	 = —— - — 1
13	13	13
22
6 :
—1 .
13 ■
Vậy phương trình có một nghiệm z = ——
(7 - 3i)z + (2 + 3i) = (5 - 4i)z (2 + i)z = -2 - 3i 
-2-3Ĩ
2 + i
(-2-3ĨX2-Ì)	7 4
z =	_	= - — - — i
5 5
Vậy phương trình có một nghiệm z = -
7 4.
— - — i.
5 5 ■
Giải phương trình z2 - 2z + 13 = 0.
Ta có: A’ = -12 = 12i2
Suy ra phương trình có hai nghiệm: Zị 2 = 1 ± 2731
Giải phương trình z4 - z2 - 6 = 0.
Đặt t = z2, ta được phương trình t2 - t - 6 = 0. Phương trình này có hai nghiệm thực = 3, t2 = -2.
tx = 3 « z = ±73
t2 = -2 « z2 = 2i2 o z = ±721
Vậy phương trình có bốn nghiệm: z = ±73,z = ±721
Trên mặt phẳng tọa độ, hãy tìm tập hợp điểm biểu diễn số phức z thỏa mãn từng bất đẳng thức:
a) |z| ‘< 2	b) |z - i| < 1	c) |z - 1 - i| < 1
Giải
Gọi M(x; y) là điểm biểu diễn của sô' phức z = X + yi (x, y G R).
a) Ta có: |z| 7x2 + y2 < 2 o X2 + y2 < 4
Vậy tập hợp các điểm M là hình tròn tâm o bán kính R = 1, không kể các điểm trên biên.
Ta có: z - i - X + (y - l)i. Do đó:
|z - i| 7x2 + (y -l)2 X2 + (y -1)2 < 1
Vậy tập hợp các điểm M là hình tròn tâm 1(0; 1), bán kính R - 1, kể các điếm trên biên.
Ta có: z - 1 - i = X - 1 + (y - l)i. Do đó:
|z -1 - i| 7(x-l)2 -+ (y -1)2 (x -1)2 + (y - l)2 <1
Vậy tập hợp các điểm M là hình tròn tâm J(l; 1), bán kính R = 1, không kể các điểm trên biên.