Giải Toán 12: Bài 4. Hàm số mũ và hàm số lôgarit

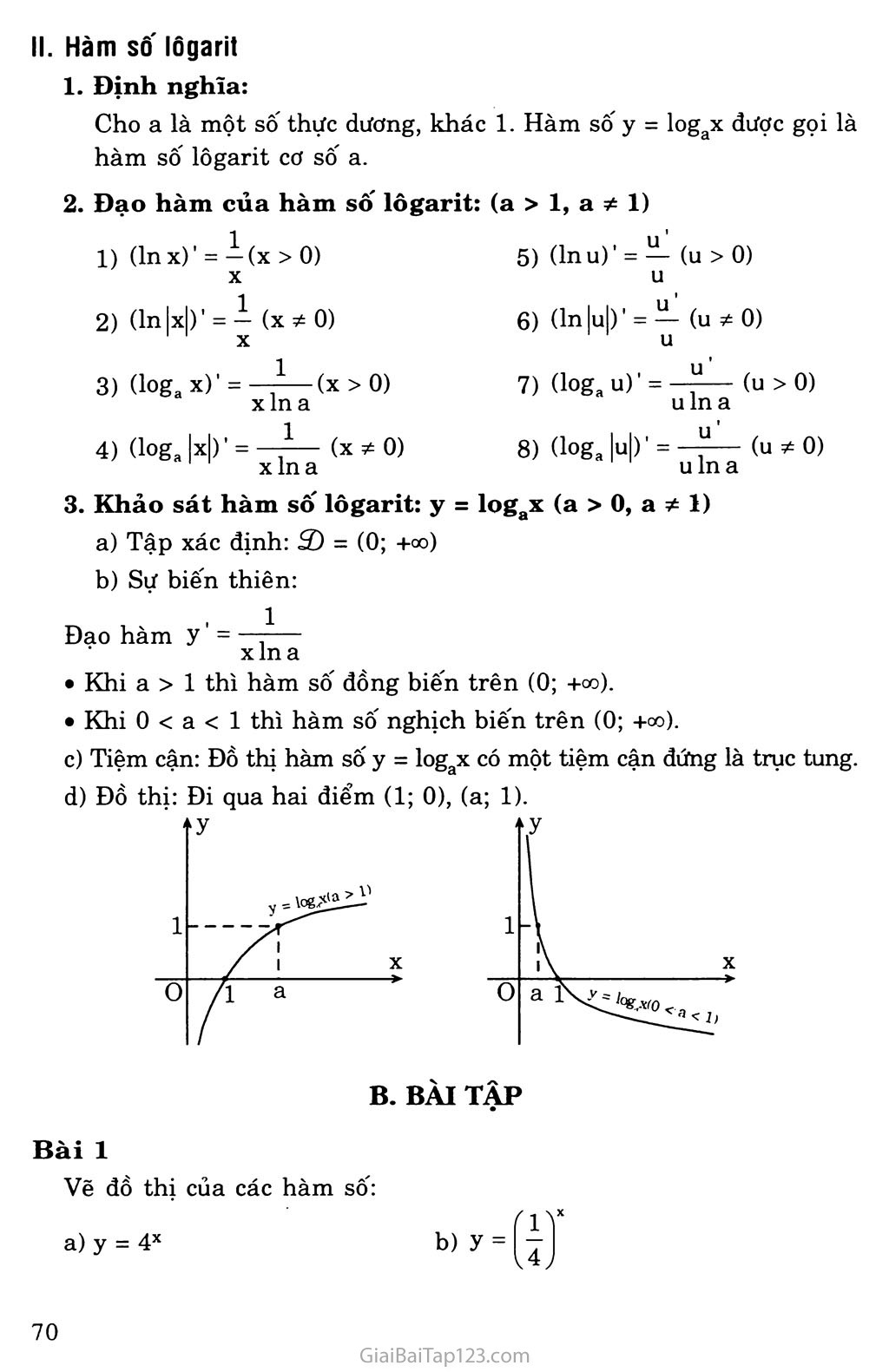
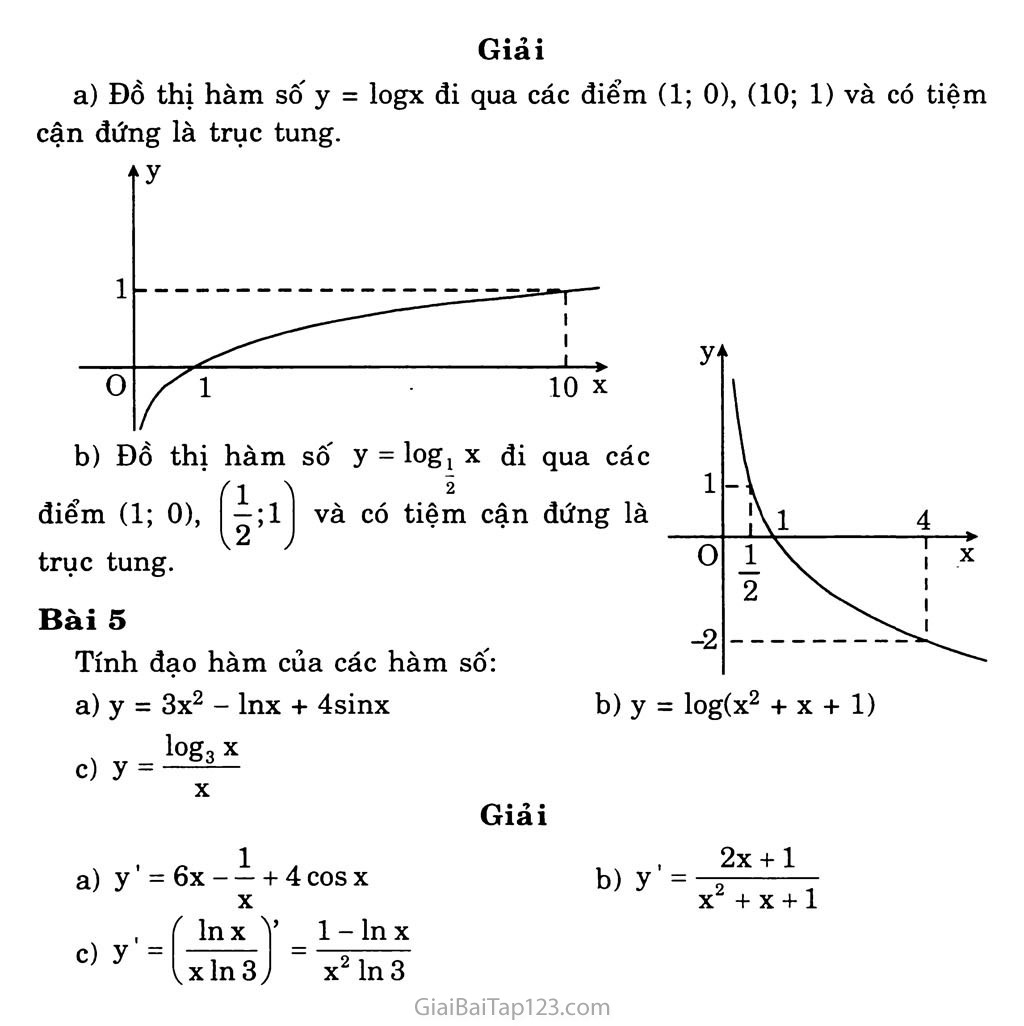
§4. HÀM SỐ MŨ - HÀM số LÒGARIT
A. KIEN THỨC CẦN NHỚ
Hàm sô' mũ
Định nghĩa
Cho a là một số thực dương, khác 1. Hàm số y = ax được gọi là hàm số mũ cơ số a.
Đạo hàm của hàm số mũ
(ex)’ = ex	3) (eu)’ = u’eu
(ax)’ = axlna (a>0, a*l)	4) (au)’ = u’aulna (a > 0, a * 1)
Khảo sát hàm số mũ: y = ax (a > 0, a 1)
Tập xác định: 3) = R
Đạo hàm: y’ = axlna
Khi a > 1 thì hàm số đồng biến trên R.
Khi 0 < a < 1 thì hàm số nghịch biến trên R.
Tiệm cận:
Đồ thị hàm số y = ax có tiệm cận ngang là trục hoành.
Đồ thị: Đồ thị hàm số y = ax đi qua hai điểm (0; 1), (1; a).
Hàm sô' lôgarit
Định nghĩa:
Cho a là một sô thực dương, khác 1. Hàm số y = logax được gọi là hàm số lôgarit cơ số a.
Đạo hàm của hàm số ỉôga
(Inx)' = — (x > 0)
x
(lnlx|)’ = - (x*0)
X
(loga x)' = 1 (x > 0)
xln a
(loga |x|)' = —5— (x * 0)
xlna
Khảo sát hàm số lôgarit: 5
Tập xác định: 2) = (0; +co)
it: (a > 1, a # 1)
(Inu)' - — (u > 0)
u
(ln|u|)' = — (u * 0)
(loga u)' = u (u > 0)
ulna
(loga |uị)' = —- (u * 0)
u In a
= logax (a > 0, a * 1)
Sự biến thiên:
Đạo hàm y' = —,—
X In a
Khi a > 1 thì hàm số đồng biến trên (0; +00).
Khi 0 < a < 1 thì hàm số nghịch biến trên (0; +00).
Tiệm cận: Đồ thị hàm số y = logax có một tiệm cận đứng là trục tung.
Đồ thị: Đi qua hai điểm (1; 0), (a; 1).
b)
B. BÀI TẬP
Bài 1
Vẽ đồ thị của các hàm số:
y = 4X
Giải
y’ = (2xex + 3sin2x)’ - 2ex(l + x) + 6cos2x
y’ = lOx + 2x(sinx - ln2.cosx)
l-(x + l)ln3
y	¥
Bài 3
Tìm tập xác định của các hàm số: a) y = log2(5 - 2x)
c) y — log/x2 -4x + 3)
5
b) y = log3(x2 - 2x)
.	 3x + 2
d) y = logo,4
Giải
Gọi S) là tập xác định của các hàm số đã cho. 	 5	_(	5
a) Điều kiện 5-2x>0c>x Jj - I co; 2
b) Điều kiện X2 - 2x > 0 (x 2) => S) = (-oo; 0) u (2; +oo)
c) Điều kiện X2 - 4x + 3 > 0 (x 3) => 3) = (-co; 1) ụ (3; +co)
d) Điều kiện
ÈL±£>0«-| S)=f-|;lì
1 - X	3	V 3 ;
Bài 4
Vẽ đồ thị của các hàm số: a) y = logx
b) y = logi X
2
b) y = log(x2 + X + 1)
Giải
a)
c)
y' = 6x - — 4- 4 cos X
X
b)
2x + l
X2 4- X 4- 1
1 - In X
X2 ln3
Giải
Đồ thị hàm số y = logx đi qua các điểm (1; 0), (10; 1) và có tiệm cận đứng là trục tung.
Đồ thị hàm số y = log1 X đi qua các điểm (1; 0), I Ệ;1 I và có tiệm cận đứng là trục tung.
Bài 5
Tính đạo hàm của các hàm số:
y = 3x2 - Inx 4- 4sinx log, X
y=—^—
X