Giải Toán 12: Ôn tập chương I

Khi m = 0 phương trình hàm số trở thành y -
Tập xác định: S) = 1R\(1Í
Sự biến thiên:
• Chiều biến thiên: y' = -—-—7 <0, Vx * 1 (x -1)
Hàm số nghịch biến trên các khoảng (-co; 1), (1; +00)
Hàm số không có cực trị.
Giới hạn:
1 + -
X
lim V = lim	— = 1 => đồ thị có tiệm cận ngang y = 1.
lim y = +CO, lim y = -co => đồ thị có tiệm cận đứng X = 1. X->1+	X—>1
• Bảng biến thiên:
y’
Đồ thị cắt trục tung tại điểm (0; -1), cắt trục hoành tại điểm (-1; 0).
Giao điểm 1(1; 1) của hai tiệm cận là tâm đối xứng của đồ thị.
Đồ thị (G) cắt trục tung tại điểm A(0; -1).
Phương trình tiếp tuyến của (G) tại có dạng:
y = y’(xA).(x - XA) + yA (*)
3
2
1
I
„	-2
Ta có: y =	.2 => y(0) = -2
(x -1)
Thế vào (*) ta được:
y = -2x - 1
Vậy phương trình tiếp tuyến của (G) tại A là y = -2x - 1.
ÓN TẬP CHƯƠNG 1
Bài 1
Phát biểu các điều kiện để hàm số đồng biến, nghịch biến. Tìm các khoảng đơn điệu của các hàm số:
y = --X3 + 2x2 - X - 7,
Giải
Phát biểu điều kiện đồng biến, nghịch biến của hàm sô.
Cho hàm số y = f(x) có đạo hàm trên K.
Nếu f(x) > 0 với mọi X thuộc K thì f(x) đồng biến trên K.
Nếu f(x) < 0 với mọi X thuộc K thì ftx) nghịch biến trên K.
Có thể mở rộng như sau:
Cho hàm số y = fíx) có đạo hàm trên K. Nếu f(x) > 0 (f(x) < 0) Vx e K và f(x) = 0 chỉ tại một số hữu hạn điểm thì hàm số đồng biến (nghịch biến) trên K.
* Tìm khoảng đơn điệu của hàm số y = -X3 + 2x2 - X - 7.
Tập xác định: 5) = R
Đạo hàm y’ = -3x2 + 4x - 1, y’ = 0 X = 1 hoặc X = —
O
y’
0+0
Vậy hàm sô' nghịch biến trên hai khoảng . . , , , , f 1.1 Ì
biến trên khoảng I 3’’1 I -
Tập xác định: 3) = R\{1Ị
\	■	-4
Đạo hàm y' = ——-X- < 0, Vx 1.
(1-X)2
Suy ra hàm sô' nghịch biến trên hai khoảng (-co; 1), (1; +<n) và không có khoảng đồng biến.
Bài 2
Nêu cách tìm cực đại, cực tiểu của hàm sô nhờ đạo hàm. Tìm các cực trị của hàm số
y = X4 - 2x2 + 2.
Giải
Cách tìm cực đại, cực tiểu. Áp dụng quy tắc sau:
Tìm tập xác định. Tính f(x).
Tìm các điểm tại đó f(x) bằng 0 hoặc f(x) không xác định.
Lập bảng biến thiên.
Từ bảng biến thiên suy ra kết luận. Khi X vượt qua điểm x0:
Nếu f(x) đổi dấu từ dương sang âm thì Xq là điểm cực đại của hàm số. Khi đó Tx0) là giá trị cực đại của hàm số.
Nếu f(x) đổi dấu từ âm sang dương thì x0 là điểm cực tiểu của hàm số.
Khi đó f(x0) là giá trị cực tiểu' của hàm số.
Tìm các cực trị của hàm số y = X4 - 2x2 + 2.
Tập xác định: ẩ) = R
Đạo hàm: f(x) = 4x3 - 4x = 4x(x2 - 1)
f(x) = 0 x(x2 - 1) = 0 (x = 0, X = -1, X = 1)
X
-00	-1
0
1	+CO
y’
- 0
+ 0 -
0 +
y
lx
2\
Vậy hàm số có XCĐ = 0, yCĐ = 2 và XCT = ±1, yCT = 1.
Bài 3
Nêu cách tìm tiệm cận ngang và tiệm đứng của đồ thị hàm số. Ap dụng để tìm các tiệm cận của đồ thị hàm số
Giải
Cách tìm tiệm cận ngang và tiệm cận đứng của hàm số y = fix).
* Tiệm cận ngang:
Tìm tập xác định 3) của hàm số: 5) phải chứa ít nhất một trong các khoảng (-co; b), (a; +co).
Tính các giới hạn lim f(x) hoặc lim f(x) hoặc lim f(x).
X->-H-C	■	X->--O	’ X->±CQ
Kết luận: Nếu ít nhát một trong các điều kiện sau được thỏa mãn lim f(x) = b hoặc lim f(x) = b hoặc lim f(x) = b
X—>+oo	’ X—>-co	’ X->±OO
thì đường thẳng y = b là đường tiệm cận ngang của đồ thị hàm số.
Tiệm cận đứng:
Tìm tập xác định S) của hàm số.
Tìm các điểm a mà tại các điểm này hàm số f(x) không liên tục và ít nhất một trong các điều kiện sau được thỏa mãn:
lim f(x) = +00 hoặc lim f(x) = -00 hoặc lim f(x) = +CO hoặc lim f(x) = -co x->a+	x->a*	x->a	x->a
thì ta kết luận đường thẳng X = a là đường tiệm cận đứng của đồ thị hàm số.
Chú ý: Ta đã biết, nếu lim f(x) = f(x0) thì hàm số f(x) liên tục tại x->x0
điểm x0, nên điều kiện trên cho thấy hàm số Kx) không liên tục tại điểm X = a.
2 + -
lim y = lim ——— = -2. Vậy đồ thị có tiệm cận ngang y = -2.
X->±00	X->±00 z
X
Bài 4
Nhắc lại sơ đồ khảo sát sự biến thiên và vẽ đồ thị của hàm sôi
(Xem lại trong mục §5 về khảo sát hàm số)
Bài 5
Cho hàm số y - 2x2 + 2mx + m - 1 có đồ thị là (CJ, m là tham số.
Khảo sát sự biến thiên và vẽ đồ thị của hàm số khi m = 1.
Xác định m để hàm số:
Đồng biến trên khoảng (-1; +co).
Có cực trị trên khoảng (-1; +co).
Chứng minh rằng (Cm) luôn cắt trục hoành tại hai điểm phân biệt với mọi m.
Giải
Khi m = 1 phương trình hàm số trở thành y = 2x2 + 2x.
Tập xác định: S) = R
Sự biến thiên:
• Chiều biến thiên: y’ = 4x + 2, y’ = 0 X = - —
ly ra:
y’ < 0 khi X e
y’ > 0 khi X e
1) .
°; - 2 I. Hàm sô nghịch biến trên khoảng
2 > +o° I • Hàm sô đồng biến trên khoảng
Cực trị: Hàm số đạt cực tiểu tại điểm X = - — ,yCT = -
Các giới hạn:
2/
1. S —; +00
2 J-
1
2’
X
-00	--ì	+00
2
y’
0	+
y
+00	+00
__Ị
2
Bảng biến thiên:
o 1
2
2
y’ = 0 X = —
m
~2
lim y = lim X2
X->±oo	X->±=o 	Đồ thị: , Tf_Ị
Đồ thị của hàm sô là một parabol, đỉnh 11 - 2 ’ 2 1’
đi qua gốc tọa độ o và có trục đối xứng là đường thẳng
1
X = - —.
2
y = 2x2 + 2mx + m - 1
(i) Định m để hàm số đồng biến trên khoảng (-1; +co). Đạo hàm y’ = 4x + 2m.
y	-	0	+
Điều kiện để hàm số đồng biến trên khoảng (-1; +00) là: v’ >0. Vx e (-1; +00) --^m>2
2
(ii) Định m để hàm số có cực trị trên khoảng (-1; +oo).
Điều kiện để hàm số có cực trị trên khoảng (-1; +co) là:
, m	
-1 m < 2
2
Phương trình hoành độ giao điểm của (Cm) với trục hoành: 2x2 + 2mx + m - 1 = 0 (*)
Biệt thức: A’ = m2 - 2m + 2 = (m - l)2 + 1 > 0, Vm
Suy ra phương trình (*) luôn có hai nghiệm phân biệt. Vậy với mọi m, đồ thị (Cm) luôn cắt trục hoành tại hai điểm phân biệt.
Bài 6
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số
f(x) = -X3 + 3x2 + 9x + 2
Giải bất phương trình f(x - 1) > 0.
Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ x0, biết rằng f’(x0) = -6.
Giải
Khảo sát hàm sô":
Tập xác định: ẩ) = R
Sự biến thiên:
Chiều biến thiên: y’ = -3x2 + 6x + 9 = 3(-x2 + 2x + 3)
y’ = 0 -X2 + 2x + 3 = 0 (x = -1 hoặc X = 3)
Suy ra:
y’ < 0 khi X e (-oo; -1) o (3; +co). Hàm số nghịch biến trên các khoảng (-oo; -1), (3; +oo).
y’ > 0 khi X e (-1; 3). Hàm số đồng biến trên khoảng (-1; 3).
Cực trị: Hàm số đạt cực tiểu tại điểm X = -1, yCT = -3 và đạt cực đại tại điểm X = 3, yCĐ = 29.
Các giới hạn:
lim y = lim X3
9
X2
2
X3
và lim y = lim X3
-1
3
X X“
2
X3
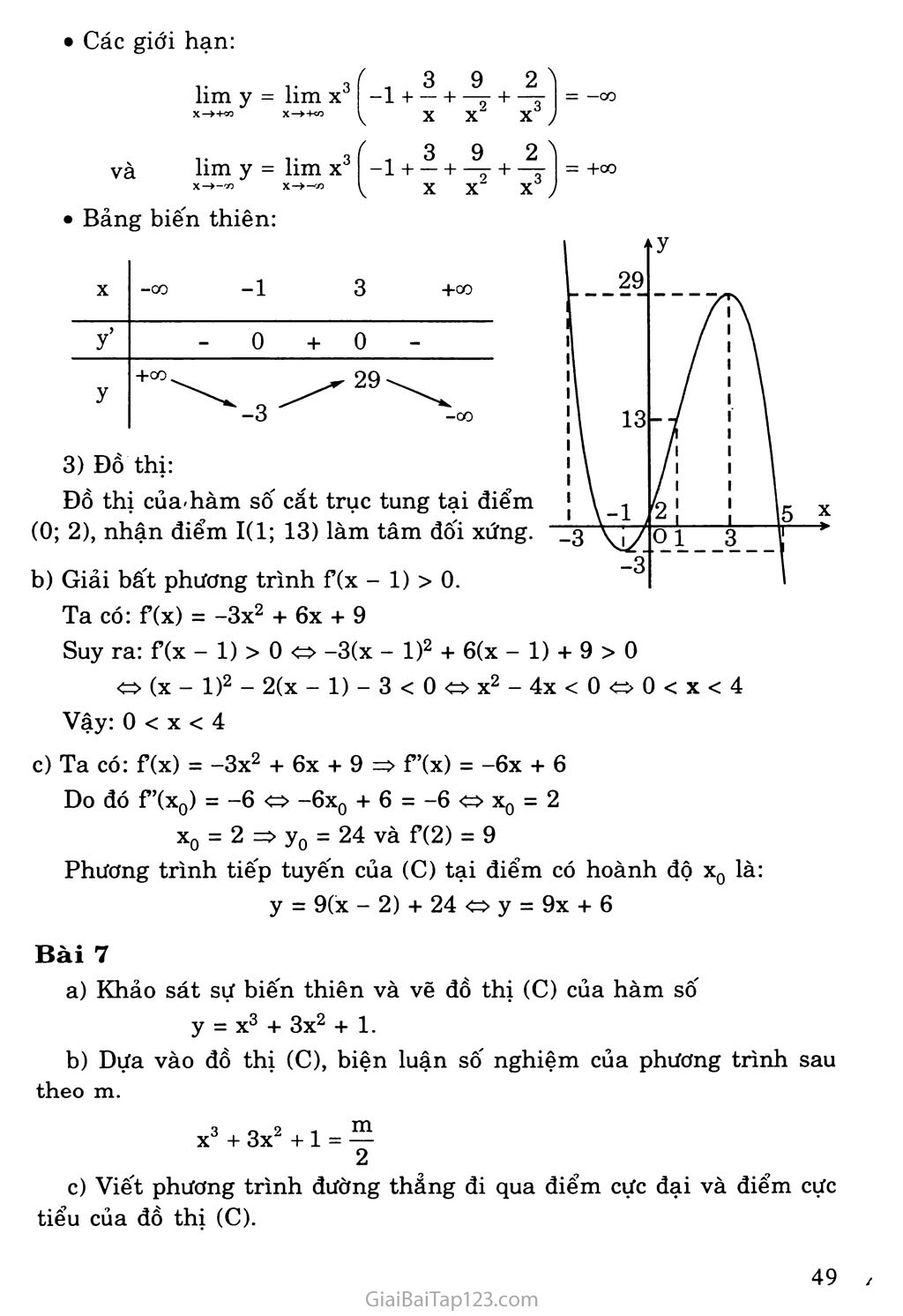
Bảng biến thiên:
Đồ thị:
Đồ thị của'hàm số cắt trục tung tại điểm (0; 2), nhận điểm 1(1; 13) làm tâm đối xứng.
Giải bất phương trình f(x - 1) > 0.
Ta có: f(x) = -3x2 + 6x + 9
Suy ra: f(x - 1) > 0 -3(x - l)2 + 6(x - 1) + 9 > 0
 (x - l)2 - 2(x -l)-3x2-4x0<x<4
Vậy: 0 < X < 4
Ta có: f(x) = -3x2 + 6x + 9 => f”(x) = -6x + 6
Do đó f’(x0) = -6 -6x0 + 6 = -6 Xq = 2
x0 = 2 => y0 = 24 và f(2) = 9
Phương trình tiếp tuyến của (C) tại điểm có hoành độ x0 là: y = 9(x - 2) + 24 y = 9x + 6
Bài 7
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số
y = X3 + 3x2 + 1.
Dựa vào đồ thị (C), biện luận số nghiệm của phương trình sau theo m.
X3+3x2+1=ạ
2
Viết phương trình đường thẳng đi qua điểm cực đại và điểm cực tiểu của đồ thị (C).
Giải
Khảo sát hàm số y = X3 + 3x2 + 1.
'Tap xaà nành : ẩ) = R
Sự biến thiên:
• Chiều biến thiên: y’ = 3x2 + 6x = 3x(x + 2)
y’ = 0 x(x + 2) = 0 (x = 0 hoặc X = -2)
Suy ra:
y’ > 0 khi X 6 (-co; -2) u (0; +oo). Hàm số đồng biến trên các khoảng (—oo; -2), (0; +oo).
y’ < 0 khi X e (-2; 0). Hàm số nghịch biến trên khoảng (-2; 0).
Cực trị: Hàm số đạt cực tiểu tại điểm X - 0, yCT = 1 và đạt cực đại tại điểm X = -2, yCĐ = 5.
Các giới hạn:
lim y - lim X3 1 + - + —- = +OO và lim y = x->+co	X—>+OT	I X	J	X—>-«
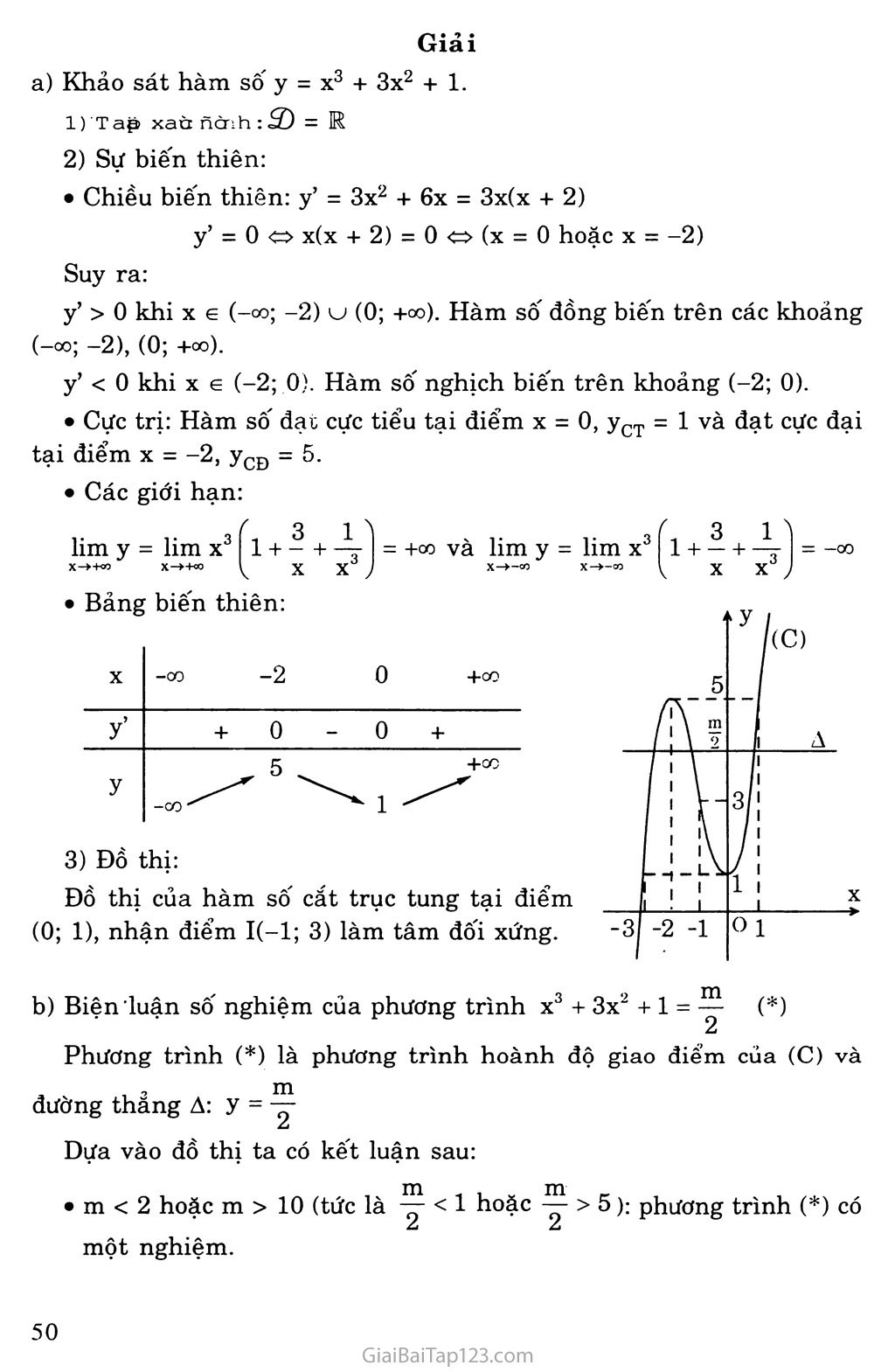
• Bảng biến thiên:
3) Đồ thị:
Đồ thị của hàm số cắt trục tung tại điểm (0; 1), nhận điểm I(—1; 3) làm tâm đốì xứng.
Biện luận số nghiệm của phương trình X3 + 3x2 + 1 =	(*)
2
Phương trình (*) là phương trình hoành độ giao điểm của (C) và
3	m
đường thăng A: y = —
Dựa vào đồ thị ta có kết luận sau:
• m 10 (tức là 5): phương trình (*) có
một nghiệm.
• m = 2 (tức là — = 1): phương trình (*) có hai nghiệm. Li
• 2 < m < 10 (tức là 1 < — < 5): phương trình (*) có ba nghiệm.
Li
• m = 10 (tức là -y = 5): phương trình (*) có hai nghiệm,
Điểm cực đại và cực tiểu của (C) là A(-2; 5), B(0; 1). Phương trình của đường thẳng qua A và B là y = -2x + 1.
Bài 8
Cho hàm số
fix) = X3 - 3mx2 + 3(2m - l)x + 1 (m là tham số)
Xác định m để hàm số đồng biến trên tập xác định.
Với giá trị nào của tham số m, hàm số có một cực đại và một cực tiểu?
Xác định m để f’(x) > 6x.
Giải
Xét hàm số f(x) = X3 - 3mx2 + 3(2m - l)x + 1.
Tập xác định: S) - R.
Đạo hàm f(x) = 3(x2 - 2mx + 2m - 1).
Điều kiện để hàm số đồng biến trên tập xác định là:
f(x) >0, Vx A’ = m2 - 2m + l(m-l)2m = l
Hàm số f(x) có một cực đại và một cực tiểu khi và chỉ khi:
phương trình f'(x) - 0 có hai nghiệm phân biệt x1;x2
f’(x) đổi dấu khi X vượt qua Xj,x2
 A’ = (m - l)2 > 0 m 1
Ta có: f(x) = 3(x2 - 2mx + 2m - 1) => f”(x) = 6(x - m)
Do đó f”(x) > 6 6(x - m) > 6x m < 0
Bài 9
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số
f(x) = ị X4 - 3x2 + Ệ
2	2
Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ là nghiệm của phương trình f’(x) = 0.
Biện luận theo tham số m số nghiệm của phương trình X4 - 6x2 + 3 = m.
Giải
I	9	3
Khảo sát hàm số y = f(x) = X4 - 3x2 + .
Tập xác định: 3) = R
Sự biến thiên:
• Chiều biến thiên: y’ = 2x3 - 6x = 2x(x2 - 3)
y’ = 0 x(x2 -3) = 0x = 0 hoặc X = +73
Suy ra:
y’ ; -73)70; 73).
y’ > 0 khi X e (-73; 0) u (73; +oo). Hàm số đồng biến trên các khoảng (-73;0),(73; +oo).
Cực trị: Hàm số đạt cực tiểu tại điểm X = ±73 , yCT = -3 và đạt
. ,.x>	. ..	3
cực đại tại điếm X = 0, yCĐ = ỹ ■
Giới hạn:
K _ i;™ ^4 fl 3	3 A	
lim y = lim X — - —5- + ——- = +co x->±~	x->±®	^2 X2	2x4 J
b) f(x) = 2x3 - 6x => f’(x) = 6(x2 - 1)
Gọi x0 là nghiệm của phương trình f”(x) = 0. Ta có:
f”(x0) = 0 6(x2 - 1) = 0 x0 = ± 1 => y0 = -1
f(l) = -4, f(-l) = 4
Phương trình tiếp tuyến tại điểm có hoành độ x0 = 1 là:
y = -4(x - 1) - 1 y = -4x + 3
Phương trình tiếp tuyến tại điểm có hoành độ x0 = -1 là:
y = 4(x + l)-ly = 4x + 3
Biện luận số nghiệm của phương trình X4 - 6x2 + 3 = m(l)
,	,	1-4	r»2	3 m
Ta có: (1) o |x4-3x2+| = ^	(2)
Phương trình (2) là phương trình hoành độ giao điểm của (C) và
,	-V.	3	... m
đường thang A: y = —
Dựa vào đồ thị ta có kết luận sau:
m
m < -6 (tức là — < -3): phương trình (1) vô nghiệm.
m = -6 (tức là — = -3): phương trình (1) có hai nghiệm.
Zu
-6 < m < 3 (tức là -3 <	< -ý): phương trình (1) có bốn nghiệm.
m = 3 ( tức là — = 3): phương trình (1) có ba nghiệm.
Zu
m > 3 (tức là — > 3): phương trình (1) có hai nghiệm.
ĩu
Bài 10
Cho hàm số
y = -X4 + 2mx2 - 2m + 1 (m là tham số) có đồ thị là (Cm).
Biện luận theo m số cực trị của hàm số.
Với giá trị nào của m thì (Cm) cắt trục hoành?
Xác định m để (Cm) có cực đại, cực tiểu.
Giải
Xét hàm số y = -X4 + 2mx2 - 2m + 1.
Tập xác đinh: S) = R
m)
x = 0
X2 — m = 0
Đạo hàm: y’ = -4x3 + 4mx = 4x(-x2
y’ = 0 x(-x2 + m) = 0
• m X = 0
Dễ thấy hàm số cố một cực trị (cực đại) tại điểm X = 0. Fx = o
• m > 0: y’ = 0 
X = ±Vĩn
Suy ra hàm số có ba cực trị (đạt cực đại tại hai điểm X = ±Vm và đạt cực tiểu tại điểm X = 0).
Phương trình hoành độ giao điểm của (Cm) và trục hoành:
-X4 + 2mx2 - 2m + 1 = 0 X4 - 2mx2 + 2m - 1 = 0	(1)
Đặt X = X2 (X > 0), phương trình (1) trở thành:
X2 - 2mX + 2m -1 = 0	(2)
Điều kiện để (Cm) cắt trục hoành là phương trình (1) có nghiệm, tức là phương trình (2) có ít nhất một nghiệm không âm.
Ta có: A’ = m2 - 2m + 1 = (m - l)2 > 0, Vm
Như thế với mọi m, phương trình (2) luôn có nghiệm.
Phương trình (2) có hai nghiệm đều âm khi và chỉ khi:
p = 2m -1 > 0 m > ỉ s = 2m m e 0
1	ịm < 0
Suy ra, với mọi m phương trình (2) có ít nhất một nghiệm không âm.
Vậy với mọi m, đồ thị (Cm) luôn cắt trục hoành.
Theo câu a), nếu m > 0 thì hàm số có cực đại và cực tiểu.
Bài 11
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số
Chứng minh rằng với mọi giá trị của m, đường thẳng y = 2x + m luôn cắt (C) tại hai điểm phân biệt M và N.
Xác định m sao cho độ dài MN là nhỏ nhất.
Tiếp tuyến tại một điểm s bất kì của (C) cắt hai tiệm cận của (C) tại p và Q. Chứng minh rằng s là trung điểm của PQ.
Giải
x	, X	„ X + 3
Khảo sát hàm sô y -	- .
X +1
Tập xác định: S) = R\{-1}
Sự biến thiên:
Giới hạn:
l+l-
lim y = lim	= 1 => đồ thị có tiệm cận ngang y = 1.
x-*±oo X-»±«5	1
1 + —
X
lim y = +00, lim y = -co => đồ thị có tiệm cận đứng X = -1.
X->(-!)*	X_»(-1)
(d\
p
I
2
1
■y sS
^3-2 -1
\ x
0
i \
-1
X
-co
-1	+CO
y’
-
-
y
1
-co
+00
1
• Bảng biến thiên:
Đồ thị cắt trục tung tại điểm (0; 3), cắt trục hoành tại điểm (-3; 0).
Giao điểm I(-l; 1) của hai tiệm cận là tâm đối xứng của đồ thị.
b) Gọi A: y - 2x + m
Phương trình hoành độ giao điểm của (C) và A:
X + 3
——7 = 2x + m 2x2 + (m + l)x + m - 3 = 0 (*) (x * -1)
Biệt thức: A = (m + l)2 - 8(m - 3) = m2 - 6m + 25 = (m - 3)2 + 16 > 0, Vm
Suy ra phương trình (*) luôn có hai nghiệm phân biệt.
Vậy với mọi giá trị của m, đường thẳng A luôn cắt đồ thị (C) tại hai điểm phân biệt M, N.
Tìm m để độ dài đoạn thẳng MN nhỏ nhất.
Gọi M(Xp y1), N(x2; y2) (x1	-1, X2 -1) thì X1 và x2 là các nghiệm
của phương trình (*).
Do M, N thuộc A nên yT = 2xx + m, y2 = 2x2 + m.
Ta có: MN = ự(x2 -Xj)2 +(y2 -yj2 = ự5(x2 - Xj)2 = x/5 |x2 - xj r= 7(m - 3)2 + 16
— —	—	
2
Suy ra: MN > 2V5
Vậy minMN = 2 Võ khi m = 3.
Ghi chú: Nếu phương trình bậc hai ax2 + bx + c = 0 (a * 0) có hai nghiệm phân biệt Xp x2 thì ta có:
I _v I _ VÃ
|x2-x,|=^
a + 3
Gọi hoành độ của s là xs = a (a * -1), suy ra ys =	.
a +1
Ta CÓ: y' =	=> y '<xs) = y '(a) = , L
(x +1)	(a +1)
Gọi (D) là tiếp tuyến của (C) tại điểm s, thì (D) có phương trình:
-2 , a 4- 3	-2 a2 + 6a +• 3
y - 	—õ (x - a) + -- y = 	—- .X + — 	——
(a + 1)	a + 1 (a + 1) (a + 1)
(D) cắt tiệm cận đứng tại p, suy ra Xp = -1.
(D) cắt tiệm cận ngang tại Q, hoành độ của Q nghiệm đúng phương trình:
= !x = 2a + l
-2 a2 + 6a + 3
-	—7 x + —	~	
(a + l)2 (a + I)2
Suy ra Xq = 2a + 1.
.	Xp + xo
Dễ thấy xs =	= a .
Vì ba điểm s, p, Q thẳng hàng, nên điều kiện trên chứng tỏ điểm s là trung điểm của đoạn thảng PQ.
Bài 12
Cho hàm số
f(x) = ịx3 -ịx2 -4x + 6.
3	2
Giải phương trình f(sinx) = 0.
Giải phương trình f”(cosx) = 0.
Viết phương trình tiếp tuyến của đồ thị hàm số đã cho tại điểm có hoành độ là nghiệm của phương trình f”(x) - 0.
Giải
Giải phương trình P(sinx) = 0.
f(x) = -|x3-^x2-4x + 6 => f(x) = X2 - X - 4
3	2
Do đó:
f(sinx) = 0 sin2x - sinx -4 = 0
Đặt t - sinx (-1 < t < 1), ta được phương trình: t2 - t - 4 = 0
™	z ,.A X	1 + VĨ7 x 1-ỰĨ7
Phương trình trên có nghiệm tj = —,t2 =	—— .
2	2
Cả hai nghiệm đều không thích hợp. Vậy phương trình vô nghiệm,
f(x) = X2 - X - 4 => f”(x) = 2x - 1. Do đó:
f "(cos x) = 0 2 cos X - 1 = 0 o cos X = ị = cos
2	3
Vậy phương trình có nghiệm X = ±-4 + k2?ĩ (k e Z).
O
Gọi M0(x0; y0) là điểm trên đồ thị, với x0 là nghiệm của phương trình f”(x) = 0.
1
	ri.47>
Suy ra Mn 4?; 44- , f 4?
°<2 12/ <2j
17
4
Ta có: f”(x0) = 0 2x0 -l = Oxo=Ệ
Phương trình tiếp tuyến của đồ thị tại Mo là:
17 (_ 1V 47	'	17. 145
y = —. X - — + —- y = —- X + ——
4 <	2 J 12	4	24
BÀI TẬP TRẮC NGHIỆM
Chọn khẳng định đúng trong các bài sau đây:
D. 2
D. 3
Số điểm cực trị của hàm số y = -/X3 - X + 7 là: O
A. 1	B. 0	c. 3
Số điểm cực đại của hàm số y = X4 + 100 là:
A. 0	B. 1	c. 2
s	A ,	_ 1 - X
3. Sô đường tiệm cận của đô thị hàm sô y =
A. 1
B. 2
< v là:
1 + X
c. 3
D. 0
4. Hàm số y =
2x	5
	„ đồng biến trên:
X + 3
B. (—ơ
c. (~3;+oo)
D. R\{-3}
Tiếp tuyến tại điếm cực tiểu của đồ thị hàm số
y = 4 X3 - 2x2 + 3x - 5
3
Song song với đường thắng X = 1
Song song với trục hoành
c. Có hệ số góc dương
D. Có hệ số góc bằng -1
Giải
Chọn B
y’ = -X2 - 1 < 0, Vx. Hàm số không có cực trị.
Chọn A
y’ = 4x3, y’ = 0 X = 0. Suy ra hàm số đạt một cực tiểu tại điểm X = 0.
Chọn B
1 — X
Đồ thị hàm số y = 7—— có một tiệm cận đứng X = -1, và một tiệm cận ngang y = -1.
Chọn c
TT' .	2x-5 z K .	11	„
Hàm sô y = có đạo hàm y - ,	0-2 > u, Vx * -3.
X + o	VX + 0)
Vậy hàm số đồng biến trong hai khoảng (-00; -3), (-3; +00).
5. Chọn B
Ta có: y’ - X3 - 4x + 3, y’ = 0 X3 - 4x + 3 - 0 
Lập bảng biến thiên, ta suy ra hàm số đạt cực tiểu tại điểm X = 3.
Điểm cực tiểu của đồ thị là A(3; -5).
Suy ra tiếp tuyến tại A song song với trục hoành.