Giải Toán 12: Bài 5. Khảo sát sự biến thiên và vẽ đồ thị của hàm số

§5. KHẢO SÁT Sự BIẾN THIÊN VÀ
VẼ ĐỔ THỊ CỦA HÀM số
A. KIÊN THỨC CẦN NHỚ
Sơ đồ khảo sát hàm số:
Tuần tự thực hiện các bước sau:
Tập xác định:
Tìm tập xác định của hàm số.
Sự biến thiên:
Xét chiều biến thiên của hàm số:
Tính đạo hàm y’;
Tìm các điểm tại đó đạo hàm y’ bằng 0 hoặc không xác định;
Xét dấu đạo hàm y’ và suy ra chiều biến thiên của hàm sô.
Tìm cực trị.
Tìm các giới hạn tại vô cực, các giới hạn vô cực và tìm tiệm cận (nếu có).
Lập bảng biến thiên.
Đô' thị:
Dựa vào bảng biến thiên và các yếu tố xác định ở trên để vẽ đồ thị.
B. BÀI TẬP
Bài 1
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số bậc ba sau:
y = 2 + 3x - X3	b) y = X3 + 4x2 + 4x
y = X3 + X2 + 9x	d) y = -2x3 + 5
Giải
Hàm số y = 2 + 3x - X3.
Tập xác định: S) = R
Sự biến thiên:
Chiều biến thiên: y’ = 3(1 - X2), y’ = 0 X = -1 hoặc X = 1
Suy ra:
y’ < 0 khi X e (-00; -1) u (1; +00). Hàm số nghịch biến trên các khoảng (-00 ; -1), (1; +00 ).
y’ > 0 khi X e (-1; 1). Hàm số đồng biến trên khoảng (-1; 1).
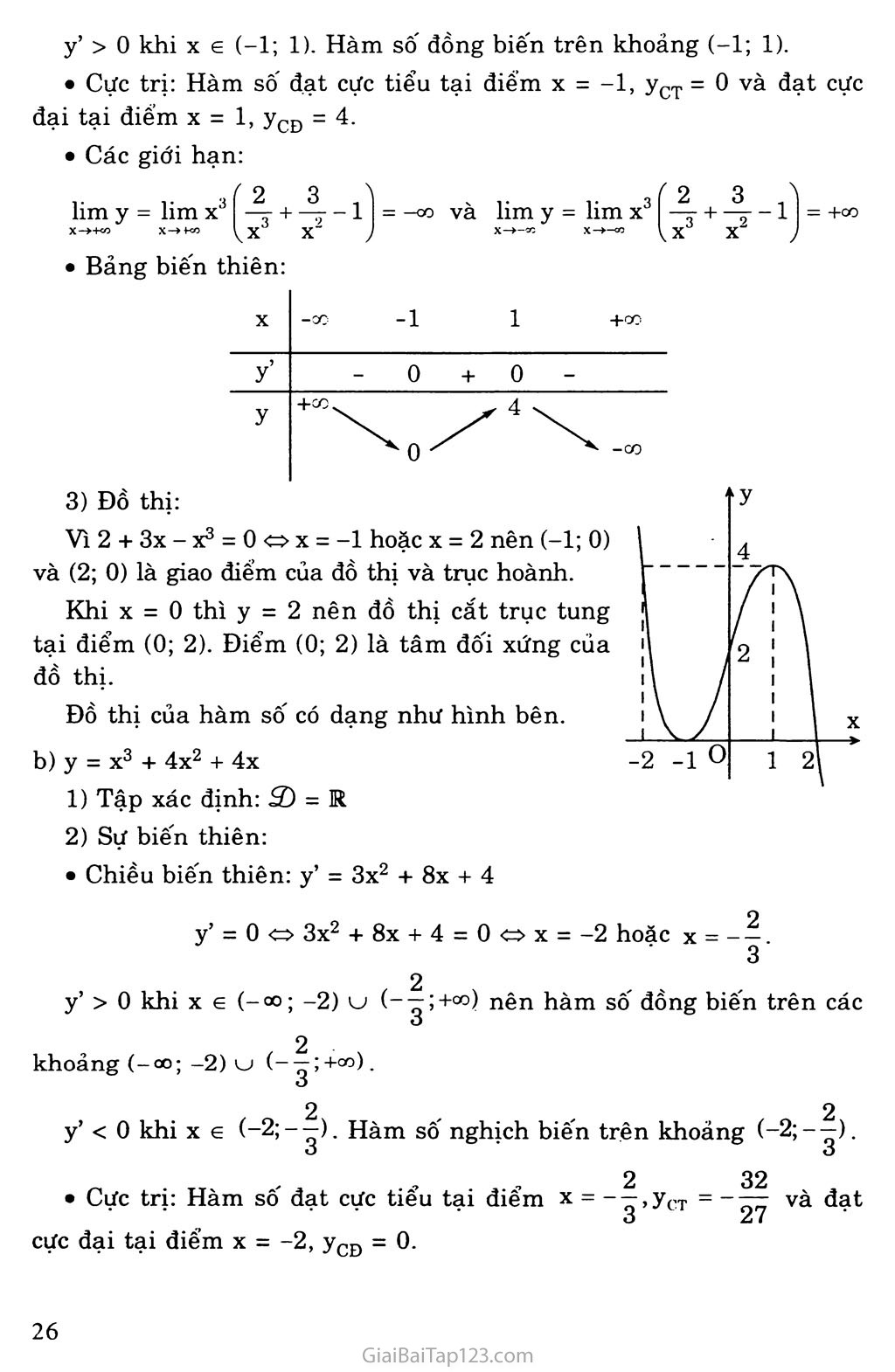
Cực trị: Hàm sô đạt cực tiểu tại điếm X - -1, yCT = 0 và đạt cực đại tại điểm X = 1, yCĐ = 4.
Các giới hạn:
af 2	3	ư 2	3
lim y = lim X' —r + — - 1 = -co và lim y = lim x‘—=- + — - l=+oo X->+«O	I X x“ /	X—>-«O	X->—co	I	/
• Bảng biến thiên:
Đồ thị:
Vì 2 + 3x-x3 = 0 o X = -1 hoặc X = 2 nên (-1; 0) và (2; 0) là giao điểm của đồ thị và trục hoành.
Khi X = 0 thì y = 2 nên đồ thị cắt trục tung tại điểm (0; 2). Điểm (0; 2) là tâm đôi xứng của đồ thị.
Đồ thị của hàm số có dạng như hình bên.
y = X3 + 4x	32
• Cực trị: Hàm số đạt cực tiểu tại điểm X = -^,yCT = và đạt O	£ í
cực đại tại điểm X = -2, yCĐ = 0.
 + 4x
Tập xác định: 2) = R
Sự biến thiên:
• Chiều biến thiên: y’ = 3x2 + 8x + 4
y’ = 0	3x2 + 8x + 4 = 0e>x = -2 hoặc X- - ị.
3
2
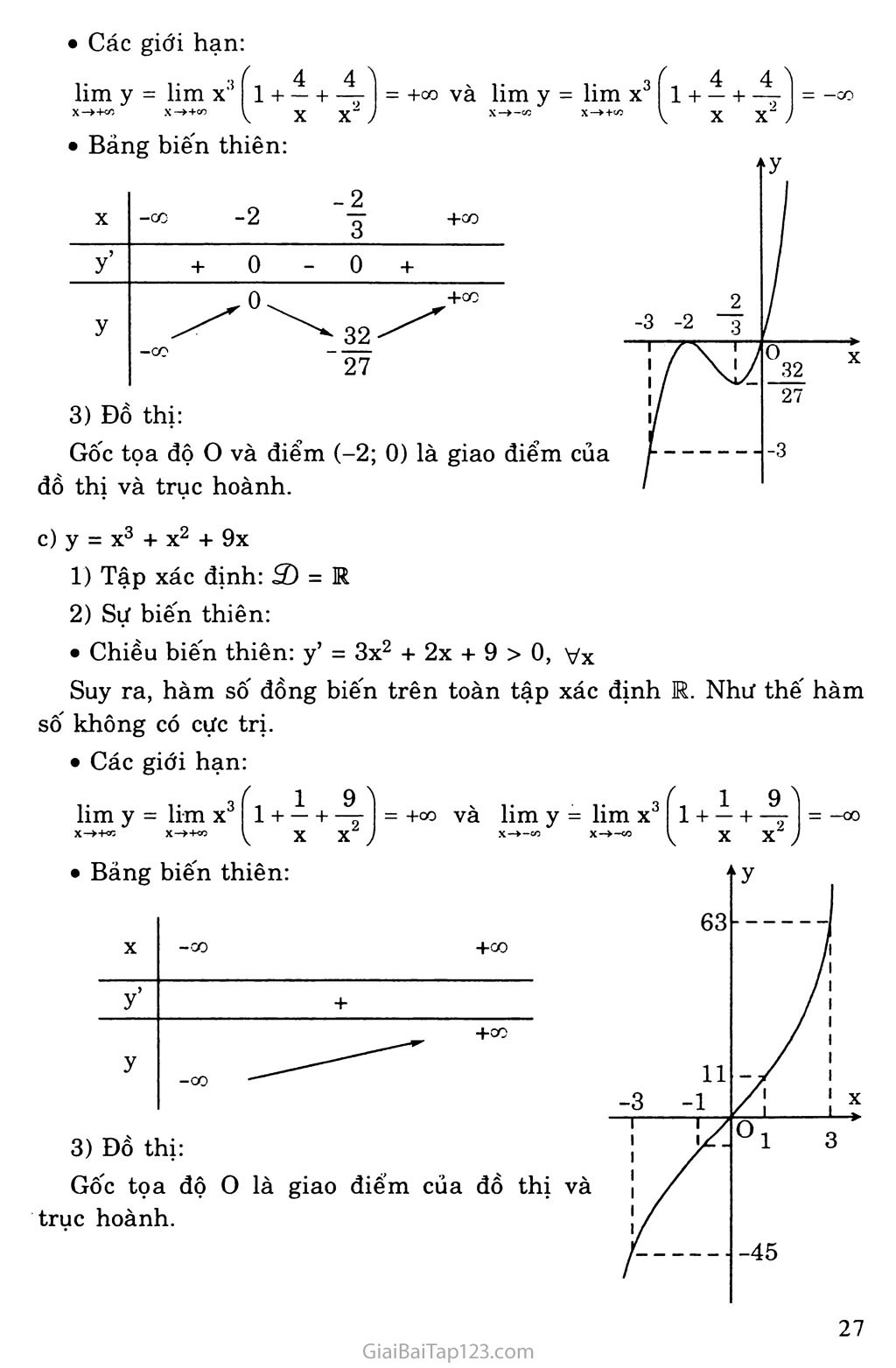
y’ > 0 khi X G (-00; -2) u (_gỉ+°o) nên hàm sô đồng biến trên các
2
khoảng (-00;-2) u (- —;+oo).
O
2.	2
y’ < 0 khi X e (-2;-—). Hàm số nghịch biến trên khoảng (-2;-—).
3
Các giới hạn:
y = X3 + X2 + 9x
Tập xác định: S) = R
Sự biến thiên:
Chiều biến thiên: y’ = 3x2 + 2x + 9 > 0, Vx
Suy ra, hàm số đồng biến trên toàn tập xác định R. Như thê hàm số không có cực trị.
Các giới hạn:
y = -2x3 + 5
Tập xác định: 3) = R
Sự biến thiên:
• Chiều biến thiên: y’ = -6x2 < 0, Vx
Suy ra, hàm số đồng biến trên toàn tập xác định R. Như thế hàm số không có cực trị.
• Các giới hạn:
b) y = X4 - 2x2 + 2
Kháo sát sự biến thiên và vẽ đồ thị của các hàm số bậc bốn sau: a) y - -X4 + 8x2 - 1
d) y = 2x2 - X4
,	1 „4 , „2	3
c) y = — X + X --T
2	2
Giải
a) y = -X4 + 8x2 - 1
Tập xác định: 3) = R
Sự biến thiên:
• Chiều biến thiên: y’ = -4x3 + 16x = 4x(-x2 + 4)
y’ = 0 x(—X2 + 4) = 0x = 0 hoặc X - ±2
Suy ra:
y’ > 0 khi X e (-00; -2) u (0; 2). Hàm số đồng biến trên các khoảng (-00;-2), (0; 2).
y’ < 0 khi X e (-2; 0) ư (2; 4-00). Hàm số nghịch biến trên các khoảng (-2; 0), (2; 4-00 ).
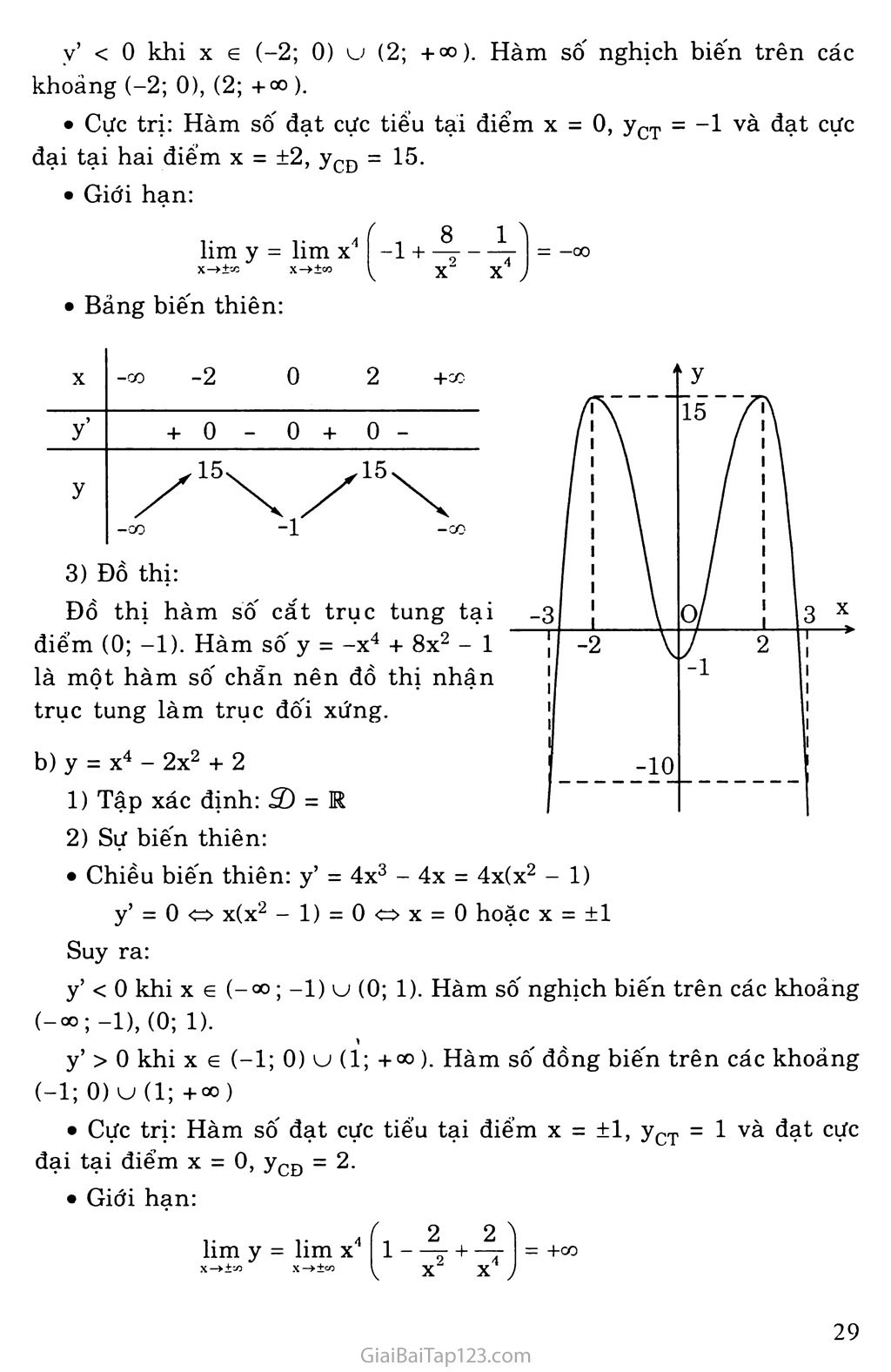
Cực trị: Hàm số đạt cực tiếu tại điểm X - 0, yCT = -1 và đạt cực đại tại hai điếm X = ±2, yCĐ - 15.
Giới hạn:
lim y = lim x'điểm (0; -1). Hàm số y = -X4 4- 8x2 - 1 là một hàm số chẵn nên đồ thị nhận trục tung làm trục đối xứng.
y = X4 - 2x2 4- 2
 	Tập xác định: 3) = R
 I -1 4-	-
X->±M	X—>±OT I
Bảng biến thiên:
y’ 4-0-04-0-
-00	-1	-co
3) Đồ thị:
Đồ thị hàm số cắt trục tung tại
X -co -2	0	2	4-co
Bảng biến thiên:
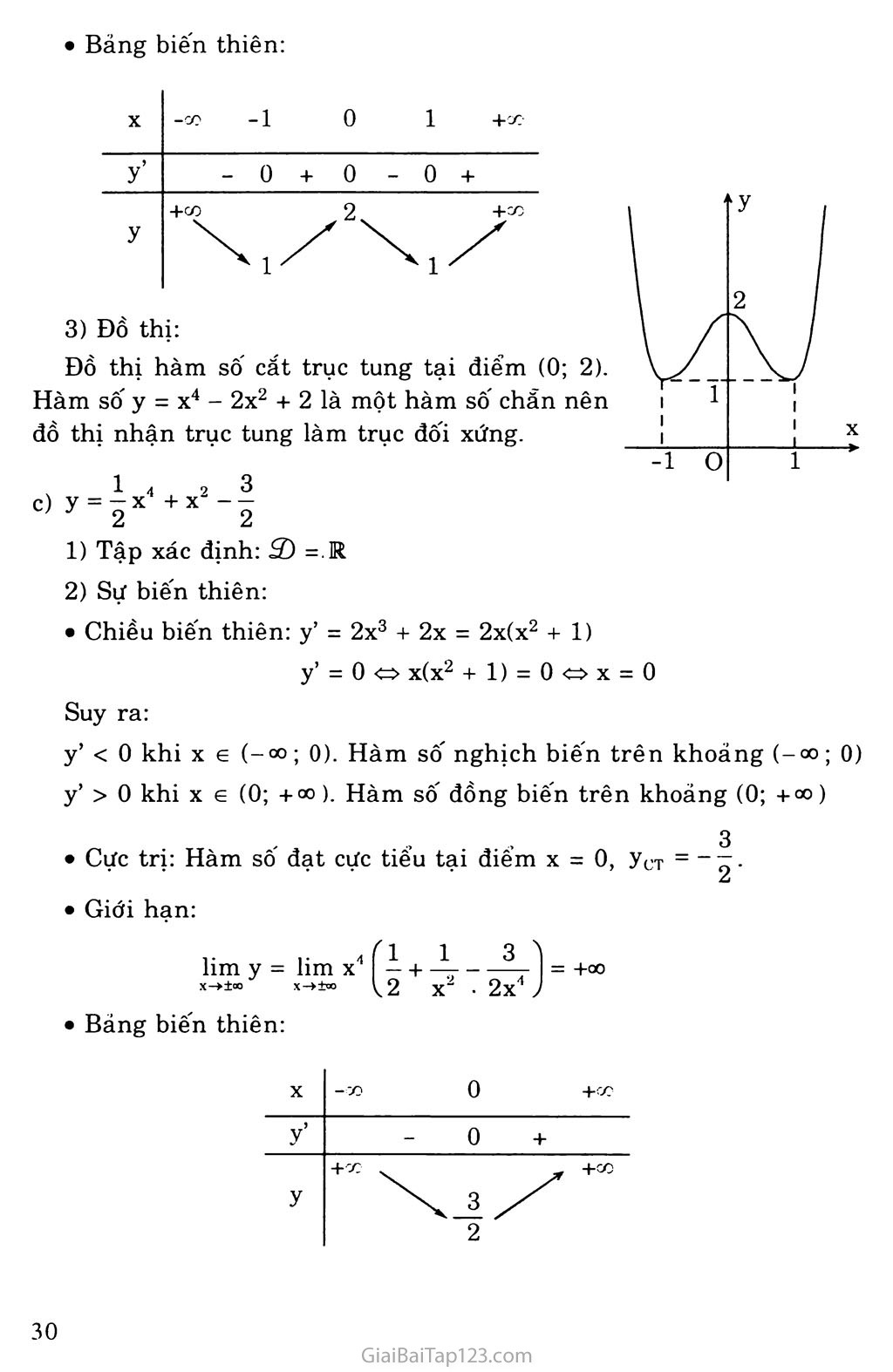
X -00	-1	0	1 +CO
y’ -0+0-0 +
Đồ thị:
Đồ thị hàm sô cắt trục tung tại điểm (0; 2). Hàm số y = X4 - 2x2 + 2 là một hàm số chẵn nên đồ thị nhận trục tung làm trục đốì xứng.
1 „4 . .2	3
y = -?x + X -■£
7	2	2
Tập xác định: S) =.R
Sự biến thiên:
• Chiều biến thiên: y’ = 2x3 + 2x = 2x(x2 + 1)
y’ = 0 x(x2 + 1) = 0 X
Suy ra:
3
2'
y’ 0 khi X e (0; +CO ). Hàm số đồng biến trên khoảng (0; +00)
Cực trị: Hàm số đạt cực tiểu tại điểm X = 0, yCT = -
• Giới hạn:
„4(1 1	3 ì_
lim y = lim X — + —- - ——- = +00 x~>±"	2 X2 ■ 2x‘ J
• Bảng biến thiên:
X
-co
0
4-co
y’
-
0
+
y
+0O
k_3 z
2
yr +cc
Đồ thị:
Đồ thị cắt trục tung tại điếm (0;- ~r) và cắt trục hoành tại hai điểm (-1; 0), (0; 1).
nên đồ thị nhận trục tung làm trục đối xứng.
cực tiểu.
y = -2xy-
 - XKhảo sát sự biến thiên và vẽ đồ thị của các hàm số phân thức:
 + 3
Tập xác định: S) = R
Sự biến thiên:
• Chiều biến thiên: y’ = -4x - 4x
Đồ thị:	/ \
Đồ thị cắt trục tung tại điểm (0; 3) và cắt trục /	\
hoành tại hai điểm (-1; 0), (1; 0).	|~Q—V—
Hàm số y = -2x2 - X4 + 3 là một hàm sô chẵn I 1 nên đồ thị nhận trục tung làm trục đối xứng.	I \
Bài 3
 - -4x(l + X2)
y’ = 0 x(l + X2) = 0 X = 0
Dễ thấy khi X # 0 thì y’ cùng dấu với -4x.
y’ > 0 khi xe(-a>;0). Hàm số đồng biến trên khoảng (-co; 0).
y’ < 0 khi X e (0; +00). Hàm số nghịch biến trên khoảng (0; +CO). • Cực trị: Hàm sô' đạt cực đại tại điểm X = 0, yCĐ = 3 và không đạt
(	2	3 I
Giới hạn: Jim y = Jim X4 -1 - — +	= -00
•	X->±00	X—>±co \	-yrj j
Bảng biến thiên:
Giải
Tập xác định: S) = R\{1Ị
Sự biến thiên:
,	-4
Chiều biến thiên: y - 7“ “77 < 0, Vx 1
(x-1)
Hàm số nghịch biến trên các khoảng (-00; 1), (1; +00)
Cực trị: Hàm số không có cực trị.
Giới hạn:
' l+f
lim y = lim	Y = 1 => đồ thị có tiệm cận ngang y = 1.
X—>±co	X—>±co	1
X
lim y = +00, lim y = -co => đồ thị có tiệm cận đứng X = 1. x-»r	x->r
Bảng biến thiên:
Đồ thị cắt trục tung tại điểm (0; -3) cắt trục hoành tại điểm (-3; 0).
b)
1 - 2x
y ’ 2x-4
Giao điểm 1(1; 1) của hai tiệm cận là tâm đối xứng của đồ thị.
1) Tập xác định: 3) = R\Ị2}
2) Sự biến thiên:
Chiều biến thiên: y -	. ,2 > 0, Vx 2
(2x - 4)
Hàm số đồng biến trên các khoảng (-00; 2), (2; +00)
Hàm số không có cực trị.
Giới hạn:
--2
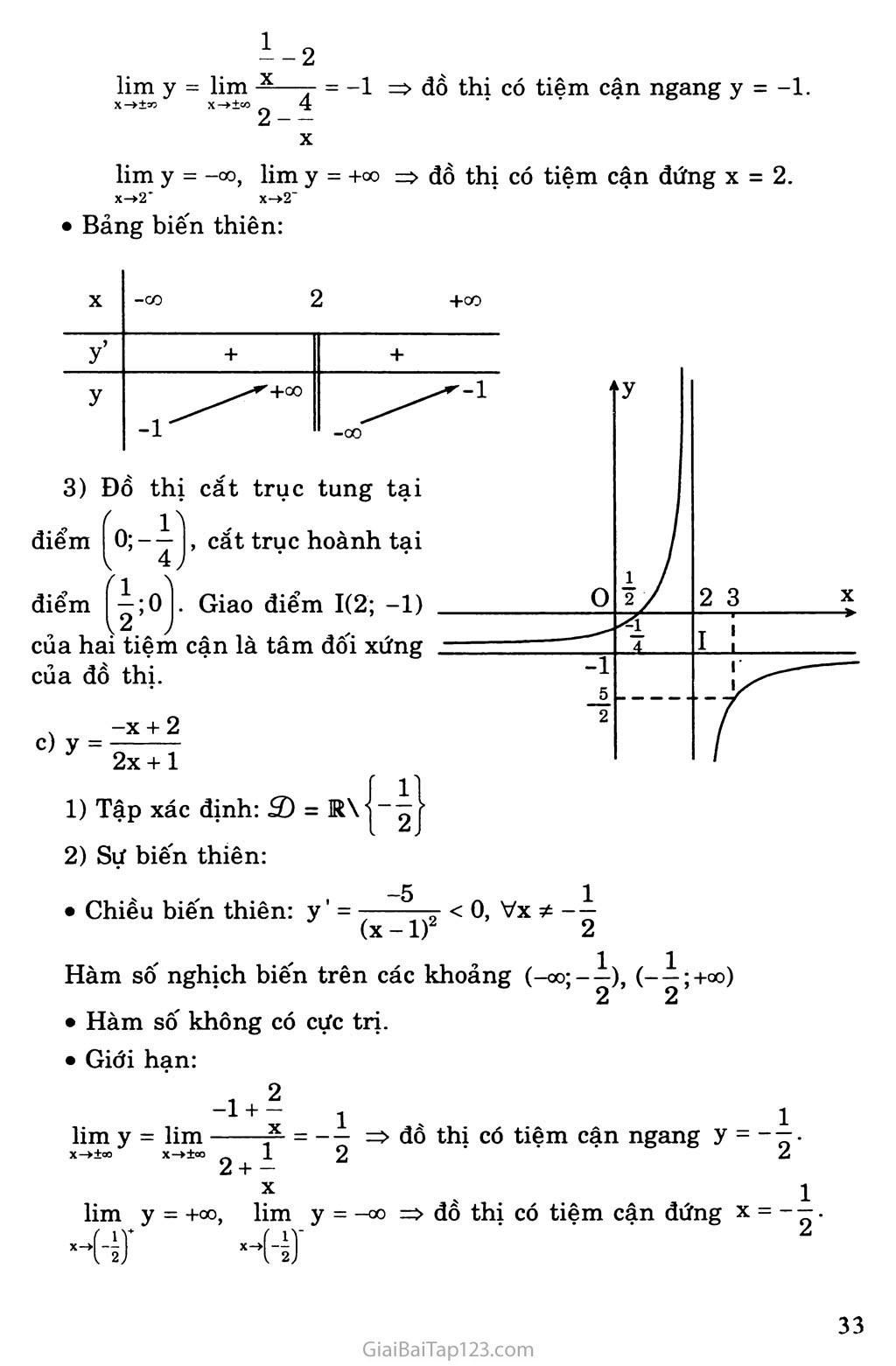
lỉm y = lim ——- = -1 => đồ thị có tiệm cận ngang y = -1. X->±eo	X->±co	4
X
lim y = -00, lim y = +00 => đồ thị có tiệm cận đứng X = 2. x-»2*	x->2“
• Bảng biến thiên:
3) Đồ thị cắt trục tung tại
điểm
cắt trục hoành tại
. Giao điểm 1(2; -1)
điểm
của hai tiệm cận là tâm đốì xứng
của đồ thị.
_ í 1]
Tập xác định: 3) = I 2 I
Sự biến thiên: • Chiều biến thiên: y' = -—7 <0, Vx *
Bảng biến thiên:
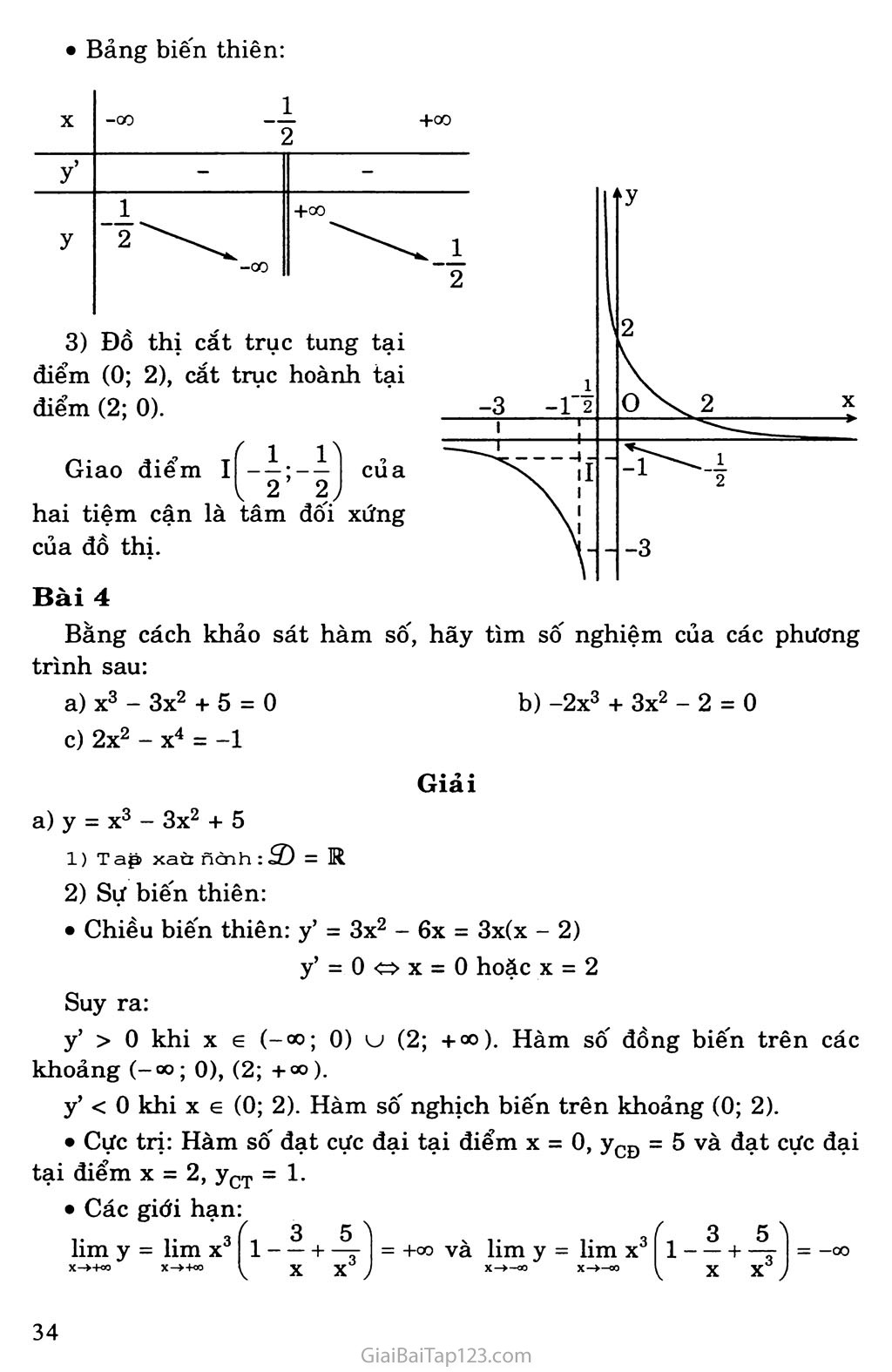
Đồ thị cắt trục tung tại điểm (0; 2), cắt trục hoành tại điểm (2; 0).
Giao điểm lí-4;-ẬÌ của l 2 2J
hai tiệm cận là tâm đối xứng của đồ thị.
Bài 4
Bằng cách khảo sát hàm số, hãy tìm số nghiệm của các phương trình sau:
X3 - 3x2 + 5 = 0 c) 2x2 - X4 = -1
-2x3 + 3x2 - 2 = 0
Giải
y = X3 - 3x2 + 5
T aịĩ xaò ãờih : S) = R
Sự biến thiên:
Chiều biến thiên: y’ = 3x2 - 6x = 3x(x - 2)
y’ = 0 X = 0 hoặc X = 2
Suy ra:
y’ > 0 khi X e (-00; 0) u (2; +oo). Hàm số đồng biến trên các khoảng (-00; 0), (2; +00).
y’ < 0 khi X e (0; 2). Hàm số nghịch biến trên khoảng (0; 2).
Cực trị: Hàm số đạt cực đại tại điểm X = 0, yCĐ = 5 và đạt cực đại tại điểm X = 2, yCT = 1.
Các giới hạn:
lim y = lim X31	1	+ —Y I =	+oo và lim y -	lim X31	1 - —	+ -^- I	= -00
x->4-oo X—>+—oo	X—>—oo I X	1
Bảng biến thiên:
y’
-00
Đồ thị:
đối xứng là điểm 1(1; 3).
Dựa vào đồ thị ta thấy, đồ thị cắt trục hoành
Đồ thị cắt trục tung tại điểm (0; 5) và có tâm tại một điểm duy nhất, ta suy ra phương trình
X3 - 3x2 + 5 = 0
có một nghiệm duy nhất thuộc khoảng (-2; -1).
y = -2x3 + 3x2 -2
Tập xác định: 3) = R
Sự biến thiên:
• Chiều biến thiên: y’ = -6x2 + 6x = 6x(-x + 1)
y’ = 0 X = 0 hoặc X = 1
Suy ra:
y’ < 0 khi X 6 (-00; 0) u (1; +00). Hàm số nghịch biến trên các khoảng (-00 ; 0), (1; +00 ).
y’ > 0 khi X e (0; 1). Hàm số đồng biến trên khoảng (0; 1).
Cực trị: Hàm số đạt cực tiểu tại điểm X = 0, yCT = -2 và đạt cực đại tại điểm X = 1, yCĐ = -1.
Các giới hạn:
<	32^	f 3	2
lim y = lim X3 -2 + — - —ụ = -00 và lim y = lim X3 -2 + — - —^- = +co X—>+co	X—>4-00	I	X X 7	X-+-O0	X—>-00 I	X	7
0
Bảng biến thiên:
y’
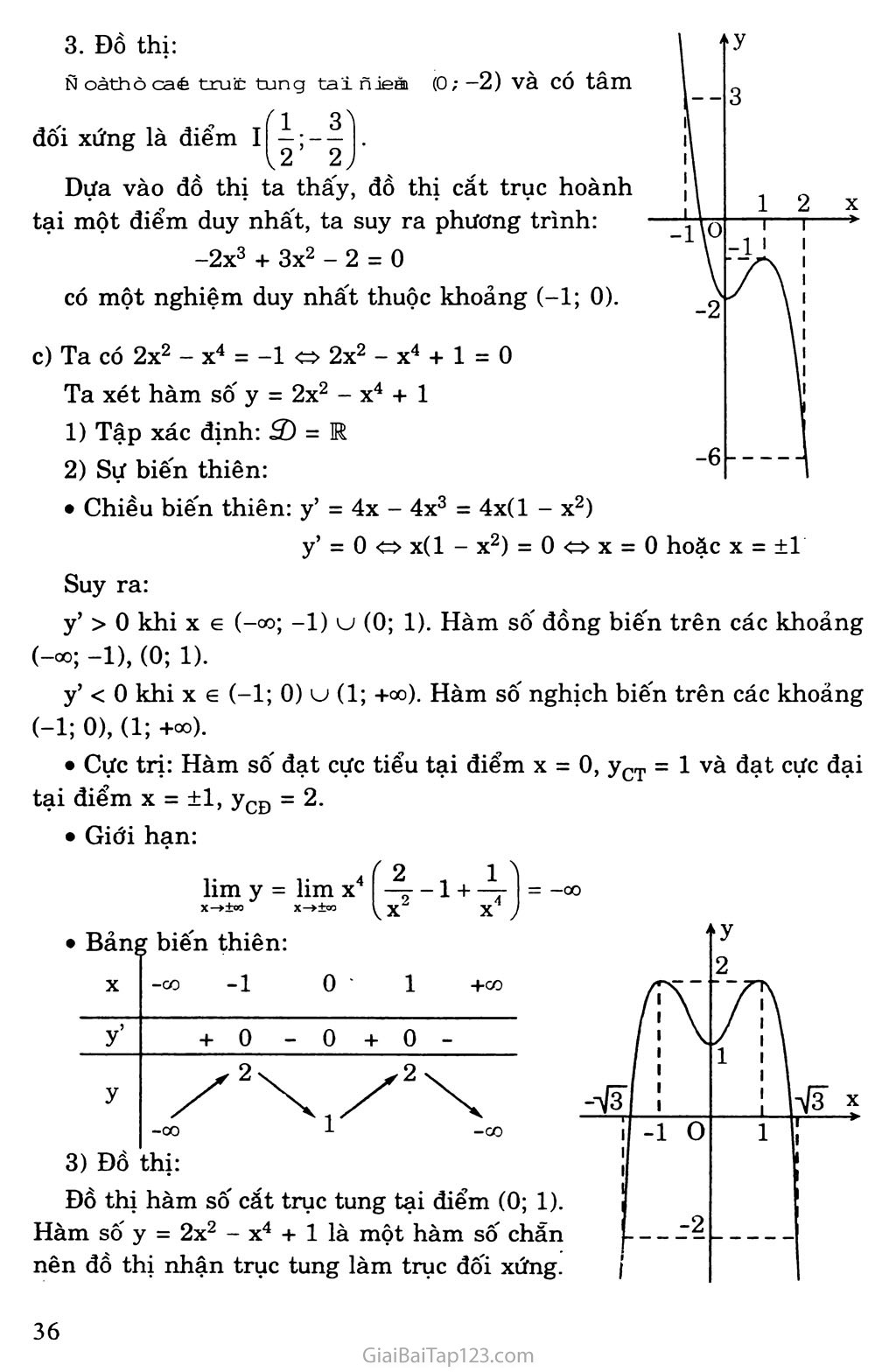
Đồ thị:
N oàthò caé truió tung tai n jeă (0 ; —2) và có tâm
Dựa vào đồ thị ta thấy, đồ thị cắt trục hoành tại một điểm duy nhất, ta suy ra phương trình:
-2x3 + 3x2 -2 = 0
có một nghiệm duy nhất thuộc khoảng (-1; 0).
Ta có 2x2 - X4 = -1 2x2 - X4 + 1 = 0
Ta xét hàm số y = 2x2 - X4 + 1
Tập xác định: 3) = R
Sự biến thiên:
Chiều biến thiên: y’ = 4x - 4x3 = 4x(l - X2)
y’ = 0 x(l - X2) = 0 X = 0 hoặc X = ±1
Suy ra:
y’ > 0 khi X G (-co; -1) u (0; 1). Hàm số đồng biến trên các khoảng (-00; -1), (0; 1).
y’ < 0 khi X e (-1; 0) u (1; +co). Hàm số nghịch biến trên các khoảng (-1; 0), (1; +00).
Cực trị: Hàm số đạt cực tiểu tại điểm X = 0, yCT = 1 và đạt cực đại tại điểm X = ±1, yCĐ = 2.
Giới hạn:
Dựa vào đồ thị ta thấy, đồ thị cắt trục hoành tại hai điểm phân biệt, do đó phương trình:
2x2 - XKhi X = 0 thì y = 1 nên đồ thị cắt trục tung tại điểm (0; 1). Điểm (0; 1) là tâm đối xứng của đồ thị.
 + 1 = 0 2x2 - X4 = -1
có hai nghiệm phân biệt.
Bài 5
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số
y = -X	Đồ thị:
 + 3x + 1.
Dựa vào đồ thị (C), biện luận về số nghiệm của phương trình sau theo tham số m
X3 - 3x + m = 0.
Giải
Khảo sát hàm số y = -X3 + 3x + 1.
Tập xác định: 3) = R
Sự biến thiên:
Chiều biến thiên: y’ = 3(1 - X2), y’ = 0 o X = -1 hoặc X = 1
Suy ra:
y’ < 0 khi X e (-co; -1) u (1; +oo). Hàm số nghịch biến trên các khoảng (-oo; -1), (1; +co).
y’ > 0 khi X e (-1; 1). Hàm số đồng biến trên khoảng (-1; 1).
Cực trị: Hàm số đạt cực tiểu tại điểm X = -1, yCT = -1 và đạt cực đại tại điểm X = 1, yCĐ = 3.
Giới hạn:
f 3	1 A	■>(	3	1 A
lim y = lim X3 -1 +	+ -r = -00 và lim y = lim X3 -1 +	+ -3 = +00
X-+-W5	X->+«5	X xơ 7	x->-»	X X 7
Bảng biến thiên:
X
-00
0
1
+CO
y’
0
+ 0
-
y
+co X
-1z
3 X
-oo
Biện luận số nghiệm của phương trình X3 - 3x + m = 0.
Ta có: X3 - 3x + m = 0 o -X3 + 3x+l = m + l
Do đó số nghiệm của phương trình đã cho là số điểm chung của đồ thị (C) và đường thẳng A: y = m + 1
Dựa vào đồ thị ta có kết quả sau:
+ Nếu m + lm<-2 thì phương trình có một nghiệm.
+ Nếu m + l = -lm = -2 thì phương trình có hai nghiệm phân biệt.
+ Nếu -1 -2 < m < 2 thì phương trình có ba nghiệm
phân biệt.
+ Nếu m + l = 3om = 2 thì phương trình có hai nghiệm phân biệt.
+ Nếu m + l>3m>2 thì phương trình có một nghiệm.
Bài 6
Cho hàm số
mx -1 y =	_
2x + m
Chứng minh rằng với mọi giá trị của tham số m, hàm số luôn đồng biến trên mỗi khoảng xác định của nó.
Xác định m để tiệm cận đứng của đồ thị đi qua A(-l;>/2)-
Khảo sát sự biến thiên và vẽ đồ thị của hàm số khi m = 2.
Giải
mx -1
2x + m
Tập xác định:
m
2~
m2 + 2 (2x + m)2
Đạo hàm: y -
0, Vx *
2
Vậy hàm số y
luôn đồng biến trên các khoảng xác định
của nó là
mx -1
2x + m
Xét hàm số
lim y = +CO nên đồ thị của hàm số có
Do lim y = -00 và
(mA
"T J
_	 m
tiệm cận đứng X = - —.
Tiệm cận đứng này đi qua điểm A(-l;x/2) khi và chỉ khi:
XU
= -1 m = 2
2	2x -1
Khi m = 2, phương trình của hàm số trở thành y =
Tập xác định: S) = R\{-1}
Sự biến thiên:
6
• Chiều biến thiên: y' = —— „.2 > 0, Vx * -1
(2x + 2)2
Hàm số đồng biến trên các khoảng (-co; -1), (-1; +00).
Hàm số không có cực trị.
Giới hạn:
= 1 => đồ thị có tiệm cận ngang y = 1.
2- —
lim y = lim	
X“>±00	X—>±03	Z
2 + —
X
X
-00	-1	+00
y’
+
+
y
^^>^+=0
1
-co
• Bảng biến thiên:
lim y = -00, lim y = +co => đồ thị có tiệm cận đứng X = -1. x->(-i)+	x->(-ir
Đồ thị cắt trục tung tại điểm I 0;- 2 I, cắt trục hoành tại điểm ^2 ’ o] ■
Giao điểm I(-l; 1) của hai tiệm cận là tâm đối xứng của đồ thị.
Bài 7
Cho hàm số
„ _ 1 4 , 1 2 L _ y = — X + —x+m
4	2
Với giá trị nào của tham số m, đồ thị của hàm số đi qua điểm (-1; 1)?
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số khi m = 1.
Viết phương trình tiếp tuyến của (C) tại điểm có tung độ bằng
Ịx«
4
Giải
a) Gọi (Cm) là đồ thị của hàm số y =
Đồ thị (Cm) đi qua điểm (-1; 1) khi và chỉ khi:
4 + ^- + m = l
4 2
Vậy giá trị của m cần tìm là m = -Ị-.
b) Khi m = 1, phương trình của hàm số trở thành y = — X4 + — X2 + 1.
1) Tập xác định: S) = R
2) Sự biến thiên:
• Chiều biến thiên: y’ = X3 + X = x(x2 + 1)
y’ = 0 X = 0
Khi X í 0 thì y’ cùng dấu với X.
Suy ra:
y’ 0 khi X e (0; 4-oo). Hàm số đồng biến trên khoảng (0; +co).
• Cực trị: Hàm số đạt cực tiểu tại điểm X = 0, yCT = 1 và không có cực đại.
• Giới hạn:
lim y = lim X4
j.
4
1 1
2x2 + X4
Bảng biến thiên:
X
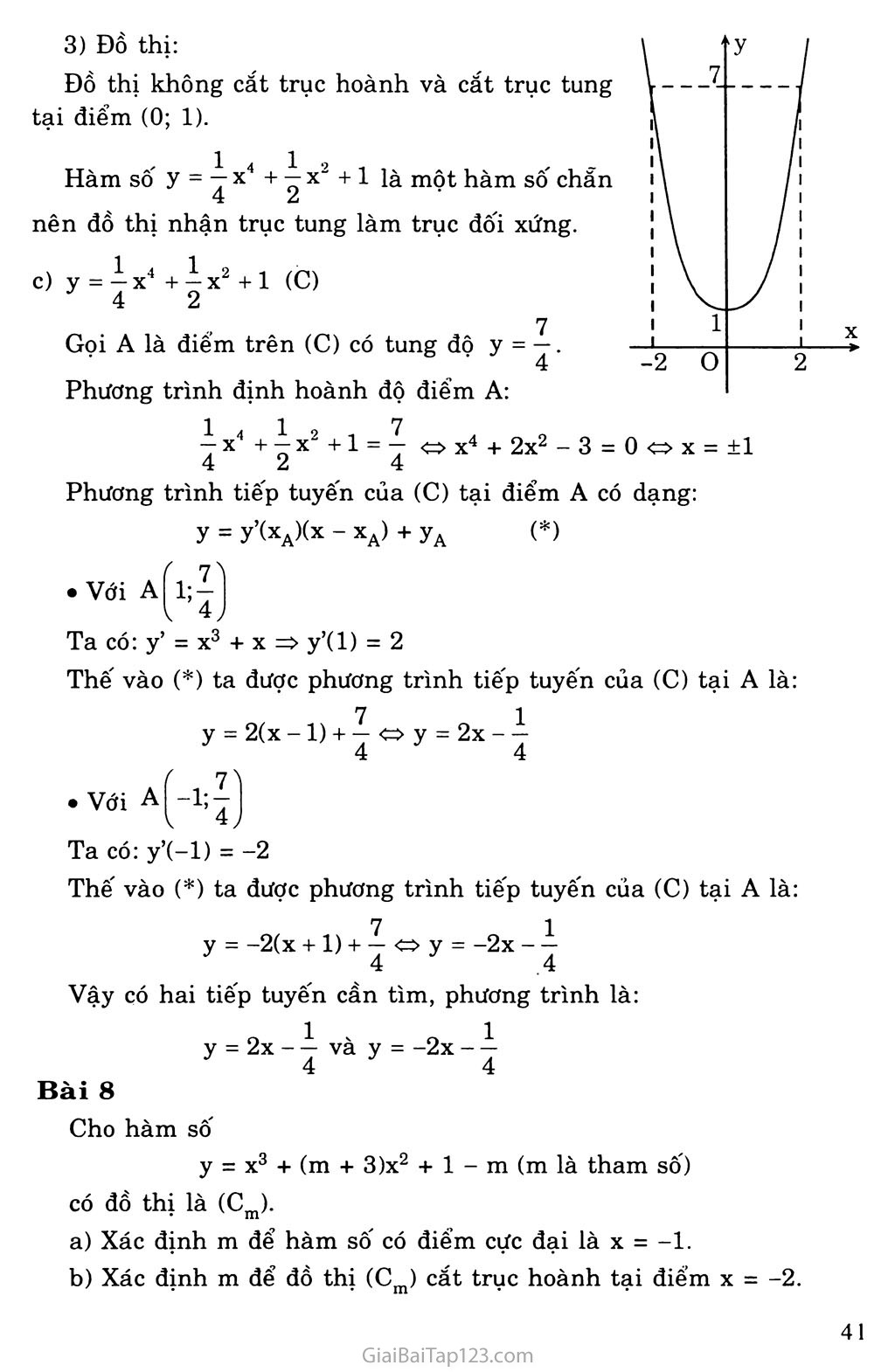
Đồ thị:
Đồ thị không cắt trục hoành và cắt trục tung tại điểm (0; 1).
Hàm số y = — X4 + — X2 + 1 là một hàm số chẵn
4	2
nên đồ thị nhận trục tung làm trục đối xứng.
y = Ậ X4 + 4 X2 + 1 (C)
4	2
Gọi A là điếm trên (C) có tung độ y = —. 4
Phương trình định hoành độ điểm A:
1 ,	1 „	7
4 X4 + 4 X2 + 1 = 4 X4 + 2x2 - 3 = 0 X = ±1
4	2	4
Phương trình tiếp tuyến của (C) tại điểm A có dạng:
y = y’(xA)(x - XA) + yA (*)
• Với A 1;4
k 4-;
Ta có: y’ = X3 + X => y’(l) = 2
Thê vào (*) ta được phương trình tiếp tuyến của (C) tại A là:
7	1
y = 2(x - 1) + 4 y = 2x - 4
4	4
• Với A -1;4
k 4;
Ta có: y’(-l) = -2
Thế vào (*) ta được phương trình tiếp tuyến của (C) tại A là:
_ 7	1
y = -2(x + 1) + 4 y = -2x - 4
4	.4
Vậy có hai tiếp tuyến cần tìm, phương trình là:
y = 2x - Ị và y = -2x - —
4	4
Bài 8
Cho hàm số
y = X3 + (m + 3)x2 + 1 - m (m là tham số)
có đồ thị là (Cm).
Xác định m để hàm số có điểm cực đại là X = -1.
Xác định m để đồ thị (Cm) cắt trục hoành tại điểm X = -2.
Giải
a) Gọi f(x) = X3 + (m + 3)x2 + 1 - m
Đạo hàm f(x) = 3x2 + 2(m + 3)x
Dấu hiệu cần để íĩx) đạt cực đại tại điểm X = -1 là:
3 f(-l) = 0 « 3 - 2(m + 3) = 0 m =
3 Khi m ~ 2	= 3x2 + 3x.
f(x) = 0 X = 0 hoặc X = -1
X
—00
-1
0
+00
f(x)
+
0
0
+
Suy ra fix) đạt cực đại tại điểm X = -1.
Vậy m = - —.
2
b) Đồ thị (Cm) cắt trục hoành tại điểm X = -2 khi và chỉ khi:
5 f(-2) = 05 + 3m = 0^>m = -|
O
Vậy m = - Ệ.
3
Bài 9
Cho hàm số
(m + l)x-2m + l y 	-	 (m là tham số)
X -1
có đồ thị là (G).
Xác định m để đồ thị (G) đi qua điếm (0; -1).
Khảo sát sự biến thiên và vẽ đồ thị của hàm số với m tìm được.
Viết phương trình tiêp tuyến của đồ thị trên tại giao điểm của nó với trục tung.
Giải
„ . (m + l)x-2m + l
Gọi f(x) =	.
X -1
Đồ thị (G) đi qua điểm (0; -1) khi và chỉ khi:
f(0) = -! ~2mi+ 1 = -1 « -2m + l = lm = o
Vậy m - 0.