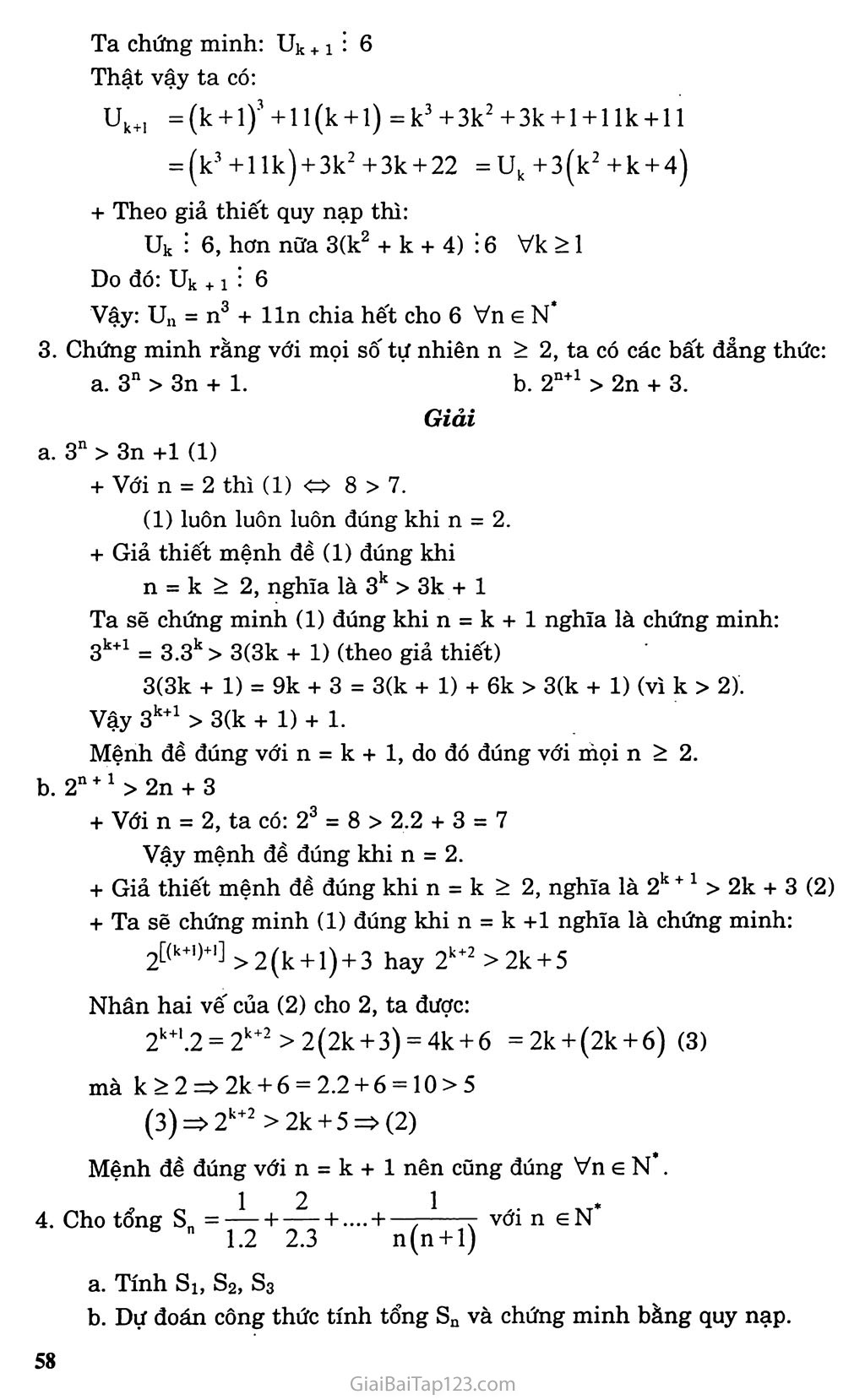Giải bài tập Toán 11 Bài 1. Phương pháp quy nạp toán học

Chương III
DÃY SỐ - CẤP SỐ CỘNG VÀ CẤP số NHÂN
Bài 1
PHƯƠNG PHÁP QUY NẠP TOÁN HỌC
A. KIẾN THỨC CẦN NAM vững
Phương pháp quy nạp toán học để chứng minh một mệnh đề chứa biến số tự nhiên gồm các bước sau:
Bước 1: Kiểm tra rằng mệnh đề đúng với n = no (thông thường no = 1 hoặc no = 0).
Bước 2: Giả thiết rằng mệnh đề đúng với sô' tự nhiên n = k (k e N, k > n0), chứng minh rằng mệnh đề đúng với n = k + 1. Kết luận mệnh đề đúng với mọi n e N , n > n0.
1. Chứng minh rằng với n e N*, ta có các đẳng thức:
B. GIẢI BÀI TẬP
(1)
„	,	, n(3n + l)
2 + 5 + 8 + .... + 3n-l =	_—-
2
b.
Ill 1
“4—- 4- — 4-... 4- ——■
2 4 8 2n
(2)
c. I2 +22 +32 + ....B2 =
n(n + l)(2n + l)
6
(3)
Giải
a. Với n = 1, ta có:
VT = 3 - 1 = 2
3+1	„
VP = -7- = 2 2
Vậy VT = VP => (1) đúng với n = 1
Giả thiết (1) đúng với n = k > 1 nghĩa là: k(3k + l)
2 + 5 + 8 + ...+ 3k-l =	7 (la)
2
Ta chứng minh (la) đúng với n = k + 1 nghĩa là chứng minh:
. . .X . (k + l)[3(k + l) + ll (k + l)(3k + 4)
2 + 5 + 8 + ... + 3k-l + 3(k + l)-l = -	71 2 i =	2
(la)<»2 + 5 + 8 + ... + 3k-l + 3(k + l)-l = k(3k + 1)+3(k + l)-l 3k2+7k + 4 _(k + l)(3k + 4)
2	-	2
=> (1) đúng với n = k + 1, vậy (la) đúng với n e N
, 1 , 1 , 1 ,	, 1	2"-1
b. — + — + — +... + —	——
2 4 8	2”	22
Với n = 1 thì:
VT = ị
2
VP=1
2
Vậy (2) đúng với n = 1
Giả sử đẳng thức đúng với n = k, tức là: 1,1,1,	,1 2k-l
~ + ~ + ~ + ... +
2 4 8 2k
„ . .. .111
2k
TZU-	, X ,	1	1 2k-l ,	1
Khi đó, ta có: —	+ -T- + -T-T =	t—T7T
2 4 8 2k 2k+ 2k 2k+' k+i _1
k+1
(2) đúng với n = k +1. Vậy nó đúng với mọi n e N
6
Khi n = 1, vế trái bằng 1
(3)
VP =
6
Vậy (3) đúng với n = 1
* Giả sử đẳng thức (3) đúng với n = k nghĩa là: l2 +22 +32 +	+ k2 = k(k + 1)(2k + 1)
6
Ta phải chứng minh (3a) đúng khi n = k + 1 + Ta cộng 2 vế của (3) cho (k + l)2
6 v
(k + l)[(k + l) + l
=	6
Vậy đẳng thức đúng với n = k + 1. Do đó, đẳng thức đúng với mọi n e N
Chứng minh rằng với n e N*
n3 + 3n2 + 5n chia hết cho 3
4n + 15n -1 chia hết cho 9
n3 +lln chia hết cho 6.
Giải
Đặt An = n3 + 3n2 + 5n
+ Ta có: với n = 1
=>Ai = l + 3 + 5 = 9:3
+ Giả sử với n = k > 1 ta có:
Ak = (k3 + 3k2 + 5k) : 3 (giả thiết quy nạp)
+ Ta chứng minh: Ak + 1 : 3
Thật vậy, ta có:
A(k+1) = (k + l)3+3(k + l)2+5(k + l)
= k3 + 3k2 + 3k +1 + 3k2 + 6k + 3 + 5k + 5
= (k3+3k2+5k) + 3k2+9k + 9
Theo giả thiết quy nạp Ak : 3, hơn nữa 9(k + 1) : 3 nên An = n3 + 3n2 + 5n chia hết cho 3 với mọi n e N*
4n + 15n - 1 chia hết cho 9
Đặt An = 4n + 15n - 1
Với n = 1 =>A1 =4 + 15-1 = 18 : 9
+ Giả sử với n = k > 1 ta có:
Ak = (4k +15k-l) : 9 (giả thiết quy nạp)
+ Ta chứng minh: Ak+1 : 9
Thật vậy, ta có:
Ak +1 =(4k +15(k + l)-l) = 4k.4‘ + 15k + 15-l
= (4k+15k-l) + (3.4k+15) = Ak+3(4k+5)
Theo giả thiết quy nạp Ak : 9, hơn nữa:
3(4k +5) ỉ 9 Vk > Inên Ak+1 ỉ 9
Vậy An = 4n + 15n -1 chia hết cho 9 Vn e N .
n3 + lln chia hết cho 6
Đặt Un = n3 + lln
+ Với n = 1 => Uị = 12:6
+ Giả sử với n = k > 1 ta có:
Uk = (k3 + llk) : 6 (giả thiết quy nạp)
Ta chứng minh: Uk +1 : 6
Thật vậy ta có:
ưk+1 = (k +1) +11 (k +1) = k3 + 3k2 +3k + 1 + 1 Ik +11
= (k3+llk) + 3k2+3k + 22 = Uk +3(k2 +k + 4)
+ Theo giả thiết quy nạp thì:
Uk : 6, hơn nữa 3(k2 + k + 4) : 6 Vk > 1
Do đó: Uk + 1 : 6
Vậy: un = n3 + lln chia hết cho 6 Vn G N’
Chứng minh rằng với mọi số tự nhiên n > 2, ta có các bất đẳng thức:
3n > 3n + 1.	b. 2n+1 > 2n + 3.
Giải
3n > 3n +1 (1)
+ Với n = 2 thì (1)	8 > 7.
(1) luôn luôn luôn đúng khi n = 2.
+ Giả thiết mệnh đề (1) đúng khi
n = k > 2, nghĩa là 3k > 3k + 1
Ta sẽ chứng minh (1) đúng khi n = k + 1 nghĩa là chứng minh: 3k+1 = 3.3k > 3(3k + 1) (theo giả thiết)
3(3k + 1) = 9k + 3 = 3(k + 1) + 6k > 3(k + 1) (vì k > 2).
Vậy 3k 1 > 3(k + 1) + 1.
Mệnh đề đúng với n = k + 1, do đó đúng với mọi n > 2.
2n + 1>2n + 3
+ Với n = 2, ta có: 23 = 8 > 2.2 + 3 = 7
Vậy mệnh đề đúng khi n = 2.
+ Giả thiết mệnh đề đúng khi n = k > 2, nghĩa là 2k + 1 > 2k + 3 (2) + Ta sẽ chứng minh (1) đúng khi n = k +1 nghĩa là chứng minh: 2C(k+I)+1] >2(k + l) + 3 hay 2k+2>2k + 5
Nhân hai vế của (2) cho 2, ta được:
2k+1.2 = 2k+2>2(2k + 3) = 4k + 6 =2k + (2k + 6) (3)
mà k > 2 => 2k + 6 = 2.2 + 6 = 10 > 5
(3) => 2k+2 > 2k + 5 => (2)
Mệnh đề đúng với n = k + 1 nên cũng đúng Vn G N . .,„12	1
Cho tổng sn = 77+ 77+ ••■• +-77—7 vớineN
1.2 2.3 n(n + l)
Tính Si, S2, S3
Dự đoán công thức tính tổng sn và chứng minh bằng quy nạp.
a.
S,=±=1_1 = 1—L
1.2 1 2 1 + 1
s 1+-M1-1L
1.2 2.3 I 2j
, _ 1 , 1 , 1
3 1.2 2.3 3.4
Giải
=1-1=1-—L
4	3 + 1
b. Dự đoán:
s, = Ậ + -^
1.2 2.3
(1)
1 + 1) n + 1
Ta chứng minh đẳng thức (1) bằng quy nạp. Với n = 1 thì (1) đúng.
Giả sử (1) đúng với n = k, ta có:
o _ 1 , 1 1
k 1.2 2.3	k(k
= l--^7
k + 1
Khi đó với n = k + 1 thì tổng vế trái của (1) là: c _ 1 , 1 1
kl 1.2 2.3	k(k
= sk
_1 X +	.	_1	1 +J	Ị__1	1
_1 k + 1 (k + l)(k + 2)_ k + 1 k + 1 k + 2	(k+1
Vậy (1) đúng với n = k + 1, do đó đúng với mọi n e N’
n(n-3)
5 Chứng minh rằng sô đường chéo của một đa giác lôi n cạnh là 	—-
Giải
Sô" đoạn thẳng (cả cạnh và đường chéo) trong một đa giác lồi n cạnh là c2n đoạn thẳng.
Suy ra số đường chéo của đa giác lồi có n cạnh là:
C2 -n
n
n! n (n-2)!(n-l)n 2!(n-2)!	2(n-2)!
n(n-l)	n2-3n n(n-3)
= —V—2 _ n =	. — = —VỊ—ỉ (đpcm).
2	2	2