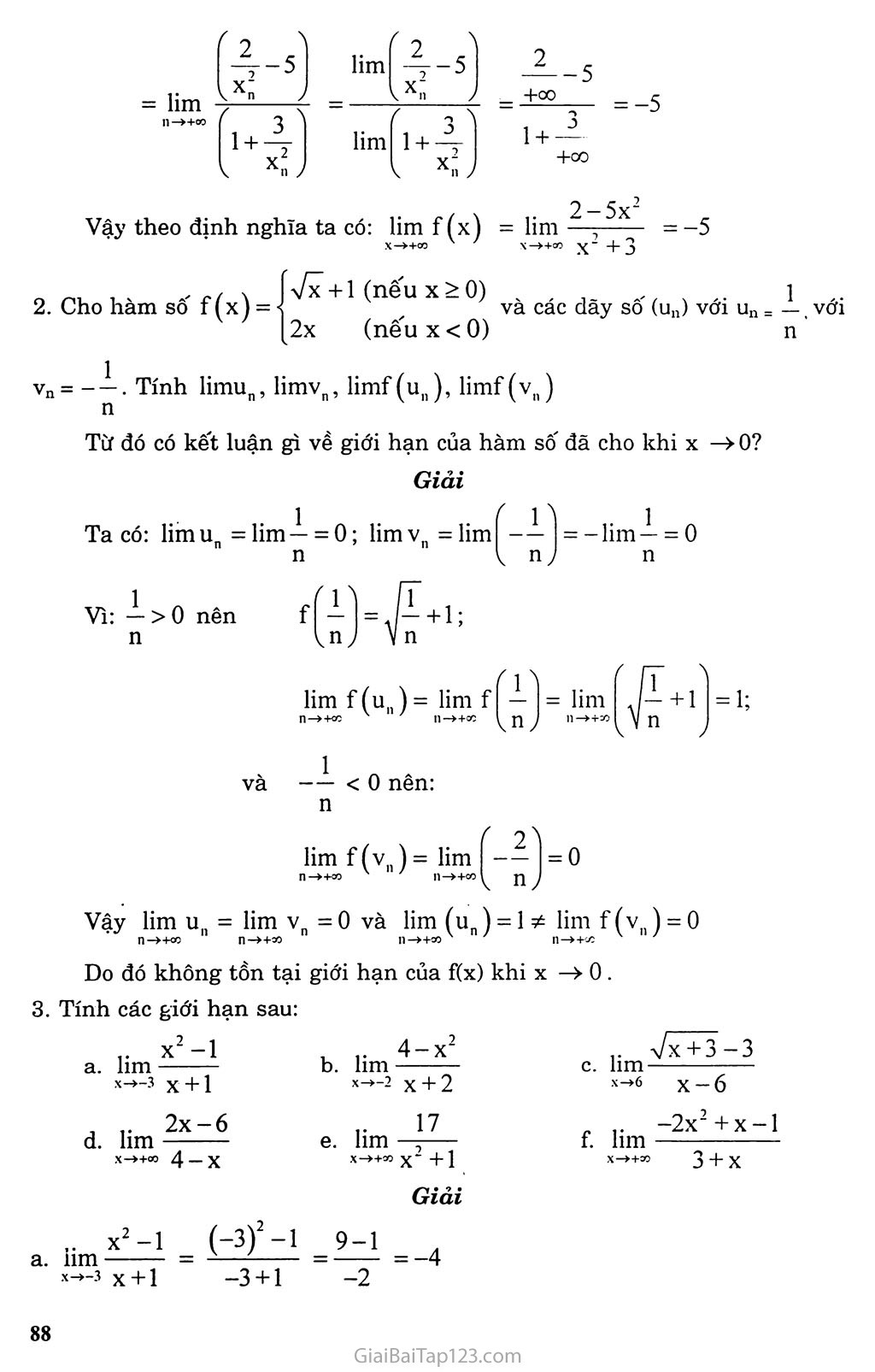Giải bài tập Toán 11 Bài 2. Giới hạn của hàm số

Bài 2
GIỚI HẠN CỦA HÀM số
A. KIẾN THỨC CẦN NAM vững
Giới hạn hữu hạn của hàm sô tại một điểm
Định nghĩa 1: Cho khoảng K chứa điểm Xo và hàm sô' y = f(x) xác định trên K hoặc trên K \ ịxo). Nếu với mọi dãy sô' (xn), xn e K \ {xol mà limxn = Xo ta đều có limf(xn) = L thì ta nói hàm sô' y = f(x) có giới hạn là sô' L khi X dần tới Xo, kí hiệu lim f(x) = L hay f(x) —> L khi X —> Xo-
Định lí 1.
a) Giả sử lim f(x) = L và lim g(x) = M thì:
X—>x(,	X—>x„
• lim [f(x)±g(x)] = L±M
x->x0
b) Nếu f(x) > 0 là lim f(x) — L là L > 0 và lim ựf(x) = VẼ.
x->x„	x->x„
Giới hạn một bên
Định nghĩa 2: Cho hàm số f(x) xác định trong khoảng (x0, b). Nếu với mọi dãy sô' (xn), xn G (x0, b) mà limxn = Xo ta đều có:
f(x) —> L thì ta nói L là giới hạn bên phải của f(x) khi X —> Xo- Khi đó ta kí hiệu: lim f(x) = L.
x-»xj
Trong trường hợp f(x) xác định trên khoảng (a, Xo), ta có lim f(x) = L (L là giới hạn bên trái của f(x) khi X —> Xo).
x->xõ
Định lí 2.
lim f(x) = L lim f(x) = lim f(x) = L
x-»x„	X-»xJ	x->x,’,
Giới hạn của hàm sô' tại vô cực
Định nghĩa 3: Cho hàm sô' f(x) xác định trên khoảng (a, + co) (khoảng (-00, a)). Nếu với mọi dãy sô' (xn) mà xn > a (xn L thì ta nói L là giới hạn của f(x) khi X —> + 00 (x —>-00).
Khi đó ta kí hiệu: lim f(x) = L I lim f(x) = L ]
X->+CO	\X->-00	Ị
hay f(x) —> L khi X —> + co (f(x) —> L khi X —> - 00)
Giới hạn vô cực của hàm sô'
Định nghĩa 4: Cho hàm sô' y = f(x) xác định trên khoảng (a, + 00) hay khoảng (—co, a). Nếu với mọi dãy sô' (xn) mà xn > a (xn +CO (x -> - 00) ta đều có íKx) -> - 00 (f(x) -> + 00) thì ta nói hàm sô' f(x) có giới hạn là - 00 (+ 00) khi xn —> + 00 (x —> - co). Khi đó ta kí hiệu:
lim f(x) =- 00 I lim f(x) = + 001
X->+cc	\x->+co	ỉ
Định nghĩa tương tự với các trường hợp khác.
Một số giới hạn đặc biệt:
lim xk = + co, k nguyên dương
X->+00
lim xk là -00 nếu k lẻ, là +00 nếu k chẵn.
X—>-00
5. Một sô' quy tắc về giới hạn vô cực a) Quỵ tắc tìm giới hạn của tích	
lim f(x)
x-»x0
lim g(x)
x->x0
lim f(x).g(x) x-»x„
L > 0
+ 00
+ 00
-00
— 00
L < 0
+ 00
— 00
— 00
+ 00
b) Quy tắc tìm giới hạn thương
limf(x)
x-^x„
lim g(x)
x->x0
Dấu của g(x)
g(x)
L
±00
Tùy ý
0
L > 0
0
+
+ 00
e —
- 00
L < 0
+
-00
—
+ 00
B. GIẢI BÀI TẬP
1. Dùng định nghĩa tìm các giới hạn sau:
.. x + 1	2-5x2
a. lim--——	b. lim—z—X-
x->4 3x-2	x->+“’ X +3
Giải
X +1 í 21
a. Đặt f(x) = -^—7-, TXĐ: D = R \ 0 3x-2	[3J
lim xn = 4
n->+00
■ 2
Xét dãy số (xn), xn G R \ và
Xét giới hạn của dãy sô': (flxn)) nếu có:
n->+co
top (xn+
n—>4-co 	
H3x„ ~2)
n—>+00 x
lim X + lim 1	4,1
n->+00	n-»+co 	' 1
lim 3xn - lim 2	12-2
n—>+õo	n—>+co
Vậy theo định nghĩa ta có: limf (x)
V —'
= lim4±l
x->4 3x - 2
b. Tương tự a:
Đặt f(x) =
2 + 5x2	„
_ , TXĐ: D = R x2+3
Xét dãy số (xn) với xn e (a;+co) và
lim xn = +00
n->+00
2_5x2
Ta có: lim f (xn) = lim — n
n—>+» v 7	II—>+co	-|- 3
X2
An
= lim —
n—>+00
■ xỉ
Ế’5
= lim
4-5
x„
2 lim V-_5
x:
X?
lim 1 + —r
x:
--5
= +c°	= -5
4-00
2 —5x2
Vậy theo định nghĩa ta có: lim f (x) = lim - ■
V xxrr.	'	V—X.' - —1_ "2
= -5
2. Cho hàm số f (x) =
VX4-1 (nếu x>0) , , _	. Ấ ..	1
và các dãy số (u„) với un - —, với
2x (nếu X < 0)	n
'n = - —. Tính limun, limvn, limf(un), limf(vn) n
Từ đó có kết luận gì về giới hạn của hàm sô' đã cho khi X —> 0?
Giải
Ta có: lim un = lim — = 0; lim vn = lim - n	k
= -lim—= 0
n
Vì: — > 0 nên
n
và
< 0 nên: n
Vậy lim un = lim
lim f (vn)= lim
3. Tính các giới hạn sau:
]• x2-l
a. lim ———
b. lini Vr
<-*-2 x + 2
a.
d.
lim
2x-6
4-x
e. lim
x->+M X +1
Giải
.. x/x + 3 -3
c. lim— 	—
X Vó X - 6
f. lim -2Vlĩzl
x->+=0	3 + X
lim
X->+00
x->-3 X + 1	-3 + 1
= ^=-4
-2
n J
V = 0 và lim (u) = 1 * lim f (vn) = 0 n '	n—X-Ur/-' '	'
Do đó không tồn tại giới hạn của f(x) khi X —> 0 .
4_x2
b. Đặt f(x) = ——7-, TXĐ: D = R \ {-2}
= 2-x
4-x2
4-x2
c. Với Vx 6, ta CÓ:
Vx + 3 -3 _ (v(x + 3) -3j(Vx + 3 +3)
X —6	(x — 6)(ựx +3 +3)
Vậy lim	—-— = lim
X—>6	x-»6
1_
6
d. lim ——- = lim
J 6
X 2- —
V X xf--l k X
2-Ế
= lim —= -2
X->+cO 4	1
X
1; 17
c. lim —-—
liml7
21 = 0
+oo
= lim
^- + 1
X
,	.	X
„ 1:	~2x2 +x-l ..
f. lim —-7—-— = lim —
= lim X. lim
X—>+co	x-*+10
i.(-2) = -co
ỉ. lim
x->r x-1
1; 2X-7
c. lim	—
*	x-1
4. Tìm các giới hạn sau:
3x-5
a. lim——-—77
Giải
3x-5
lim _
x->2(x-2)2
lim ^=2
_ 3.2-5
= (2-2)2
-5
—— = +00
0
_Ị_
0
= +co
(vì khi X —> 1 thì X -
< 0)
lim ——— = -— = -00 (vì X —> 1+ thì X - 1 > 0) x“r x-1	0
Quan sát đồ thị và nêu nhận xét về giá trị hàm số đã cho khi X -> -00, X —> 3~, X —> -3+
Kiểm tra các nhận xét trên bằng cách tính các giới hạn sau:
lim f (x) với f(x) được xét trên khoảng (-oo;-3)
X—>-00 v 7
lim f (x) với f (x) được xét trên khoảng (3; -3)
x->3“
lim f (x) với f (x) được xét trên khoảng (-3; 3)
Giải
a. Từ đồ thị thấy:
f (x) —> 0 khi X -» -co;
f (x) -> -co khi X -»3";
f (x) —> +00 khi X —> -3+ b. Ta có:
lim f (x) -	= J™ - " " - T * < - T - 0
x->-“	x->-« X -9 x->-co 2	7	2	1
X 1 —7	lim 1 —7
3 + 2
32-9
V X J	X )
lim f (x) = lim x->3“ v ’ x“rx2-9
(vì trên (3; -3) thì X2 - 9 < 0)
-1
= +00
0
f.. x + 2	-3 + 2
lim f (X) = lim —	= ———
(vì trên đoạn (-3; 3), X2 - 9 > 0)
6. Tính:
b.
c.
-2x + 5
d.
lim ————
5-2x
Giải
1 . 1
Ị_
X” X’ X4
= lim X4. lim I 1 —"V + “T _
X—>+00	X—>+co I	X X4
= +00.1 = +co
b. lim í-2x3 + 3x2 -5)= lim X3
X—>-00 V	' X—>—co
-2+ê-^
X X
I 3	5
- lim X3. lim -2+—ị-
X—♦—001	x x
-2x + 5 = lim Jx2
I I..I ,2,5
• = lim X . 1	+ —
1	V	XX
/25
= lim ịx| lim J1-—+ —7 =+00.1 =+00 X—>—co	X—>—co Y XX
d. lim x^+w 5 - 2x
= lim
+ l + x
—-—— = lim
x[--2
\ x
xí—-2
X
= lim
1-2
X
Một thấu kính hội tụ có tiêu cự là f. Gọi d và d’ lần lượt là khoảng cách từ một vật thật AB và từ ảnh A’B’ của nó tới quang tâm o của thấu kính
(hình dưới). Công thức thấu kính là ■“ + "7 = 7 •
d d' f
A'
ir;
Tìm biểu thức xác định hàm sô' d = ợ?(d).
Tìm lim (ơ(d) , lim ý?(d), lim ý9(d). Giải thích ý nghĩa của các kết
d->f’	d->f’	d->+co
quả tìm được.
Giải
,	„x. 1 . 1 _ 1	1	1	1	\ df
Ta có: . + -r = -T d =	= g(d)
d d' f	d' f d d-f
Tính:
./.X	1:„ fd f2 	
lim g(d) = lim ——- = -— = +CO (vì d - f > 0) khi d -> r) d^f 7 d-ir d - f 0
Ý nghĩa: Khi vật dẫn đến tiêu điếm nhưng lớn hơn tiêu điểm thì có ảnh ở 00.
fd
lim ợ?(d) = lim ——— = -00 (vì d - f D
d-ư- d - f
Ý nghĩa: Khi vật dẫn đến tiêu điểm nhưng ở giữa tiêu điểm và quang tâm thì có ảnh ảo ngoài vô cực.
lim ộ?(d) = lim - lim f = f
d—>+co v / d->+co — £ d—>+co	8
d
Ý nghĩa: Khi vật ở xa vô cực thì khoảng cách từ ảnh đến quang tâm bằng tiêu cực.