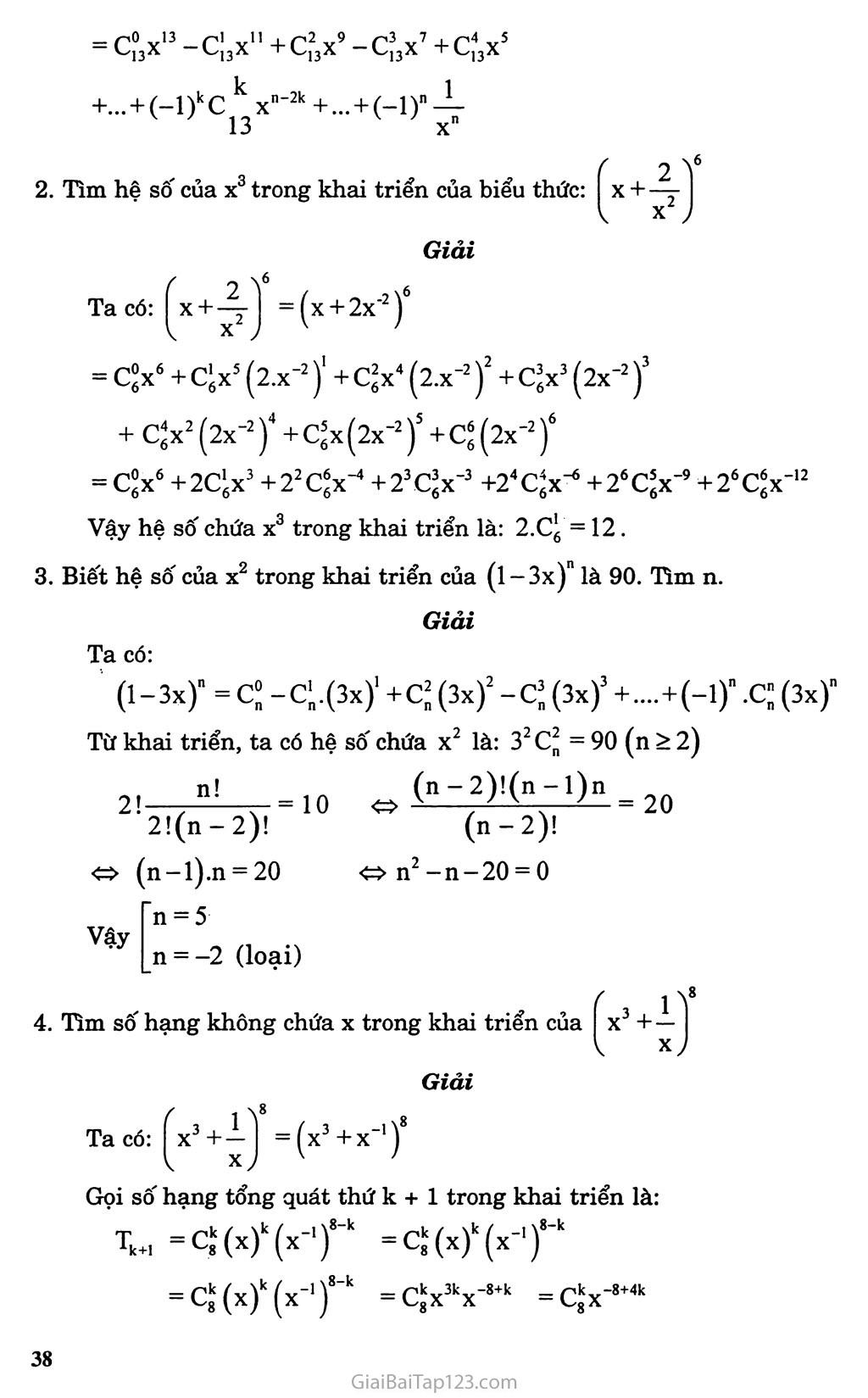Giải bài tập Toán 11 Bài 3. Nhị thức Niutơn

Bài 3
NHỊ THỨC NIU-TƠN
A. KIẾN THỨC CẦN NAM vững
Công thức nhị thức Niu-tơn
(a + b)n = c°an +C’an-'b + C^n-2b2 + ... + Ckan’kbk +... + Cnn’1abn-' +C"bn
Hệ quả: Với a = b = 1 ta có:
c° + cj, + ... + C"’1 +C" = 2n
Với a = 1, b = -1 ta có: c“+c:+...+(-i)kck+...+(-i)nc>0
Tam giác Pat-can (Pascal)
Trong công thức nhị thức Niu-tơn, cho n = 0, 1, 2,... và xếp các hệ sô’ thành dòng thì nhận được tam giác gọi là tam giác Pat-can. Ta có tam giác Pat-can như sau:
= C°3x13-Cj3x"+C23x8-k
-C33xk X?
+C	Tìm số hạng không chứa X trong khai triển của
3xGiải
+... + (-l)k c k xn’2k +... + (-1 )n 4
13	Xn
Tìm hệ số của X3 trong khai triển của biểu thức:
Giải
í 2 1/
Ta có:
x+ 2	= (x + 2x’2
< X ; v
= c°xTa có:
 + c’X5 (2.X’2)' + C2X4 (2.X-2 )2 + C3X3 (2x“2 )3
+ CgX2 (2x-2 )4 + C3x(2x’2 )5 + C* (2x‘2 )6
= CgX6 + 2CgX3 +22CgX 4 + 2 cịx"3 +24cịx"6 +26cịx’9 +26cGọi sô' hạng tổng quát thứ k + 1 trong khai triển là:
x”12
Vậy hệ số’ chứa X3 trong khai triển là: 2.Cg = 12 .
Biết hệ số của X2 trong khai triển của (1 —3x)n là 90. Tìm n.
Giải
Ta có:
(l-3x)"=C:-C'.(3x)'+C;(3x)!-Csn(3x)J+....+(-l)".C;(3x)"
Từ khai triển, ta có hệ số’ chứa X2 là: 32 C2 = 90 (n > 2)
2!—4“—=
2!(n-2)!
10
(n-2)!(n-l)n
(n-2)!
Vậy
n = 5
n = -2 (loại)
,8-k
T. . *k+l
8-k
= Ckx3kx-8+k
= Ckx-8+4k
Để có sô' hạng không chứa X trong khai triển thì: x'8+4k = x° -8 + 4k = 0 «k = 2
Vậy sô' hạng không chứa X là cị - 28 .
Tìm khai triển biểu thức (3x-4)17 thành đa thức, hãy tính tổng các hệ sô' của đa thức nhận được.
Giải
Ta có:
(3x-4)17 = c°7 (3x)17 -c;7 (3x)16 4' + c27 (3x)15 42 -C37 (3x)'4 43 + .... + C]7 (3x)'416-Cp417
=> (3x - 4)17 = 317C°7X17 -4.316 cj7x'6 + 42.315c27x14
-3!4.43c37.x14 +.... + 416.3C;7x16 — .4'7
Đặt s là tổng của các hệ sô' của đa thức bên vế phải.
Thay X = 1 vào hai vê' ta được:
s = 317.c°7 -4.3l6.cj7 + 42.315 -314.43 + L + 4,6.3.cj* -c;7.417 =(3.1-4)’
Chứng minh rằng:
1110 - 10 chia hết cho 100
1O1100 - 1 chia hết cho 10.000
là một sô' nguyên.
,— [■/	,—'100 /	,—\1OO~
c.
Giải
Ta có: ll10 = (10 + l)10 = 1O10 + Cj0109 + ... + C90 +1
=>ll,0-l = 10'° +10.109 +... + 10.10
= ioo(io8 +107 + ... + 1) chia hết cho 10.
Ta có: 1O1100 = (100 + l)100 = ÌOO100 + 100.100"+ ....+ 100.100 + 1
=>ior°°- 1 = 1002 (10098 +... + 1) chia hết cho 10000.
(1 + 7ĨÕ)'°“ - 1+c;„, 7ĨÕ+c’„ (7ĨÕ)2 +c;M pĩõỳ +...+CỈOO (Vĩõ)1 +...
=i-c;„Vĩõ+c;„(Vĩõõ)! -cfM (Vĩõ)3 +...+(-i)k (7ĩõ)k +...
/777 r /	/777 X100 /	r—— X100
710 (1 + 7ĨÕ) -(1-710)
=2-yĩõ^c;00V]õ+c;00(vrõ)3+...+cx,(Vĩõ)2m+,+...^ (*)
Với m nguyên dương sao cho 2m + 1 < 100
Trong (*) ở vế phải là tổng của các cố hạng mà mỗi số hạng là một số nguyên cfoo nhân với lũy thừa bậc lẻ của Vĩõ. Mỗi số hạng này nhân với Vĩõ ta được một số nguyên. Do đó tổng đang xét là một số nguyên.