Giải bài tập Toán 7 Bài 9. Tính chất ba đường cao của tam giác

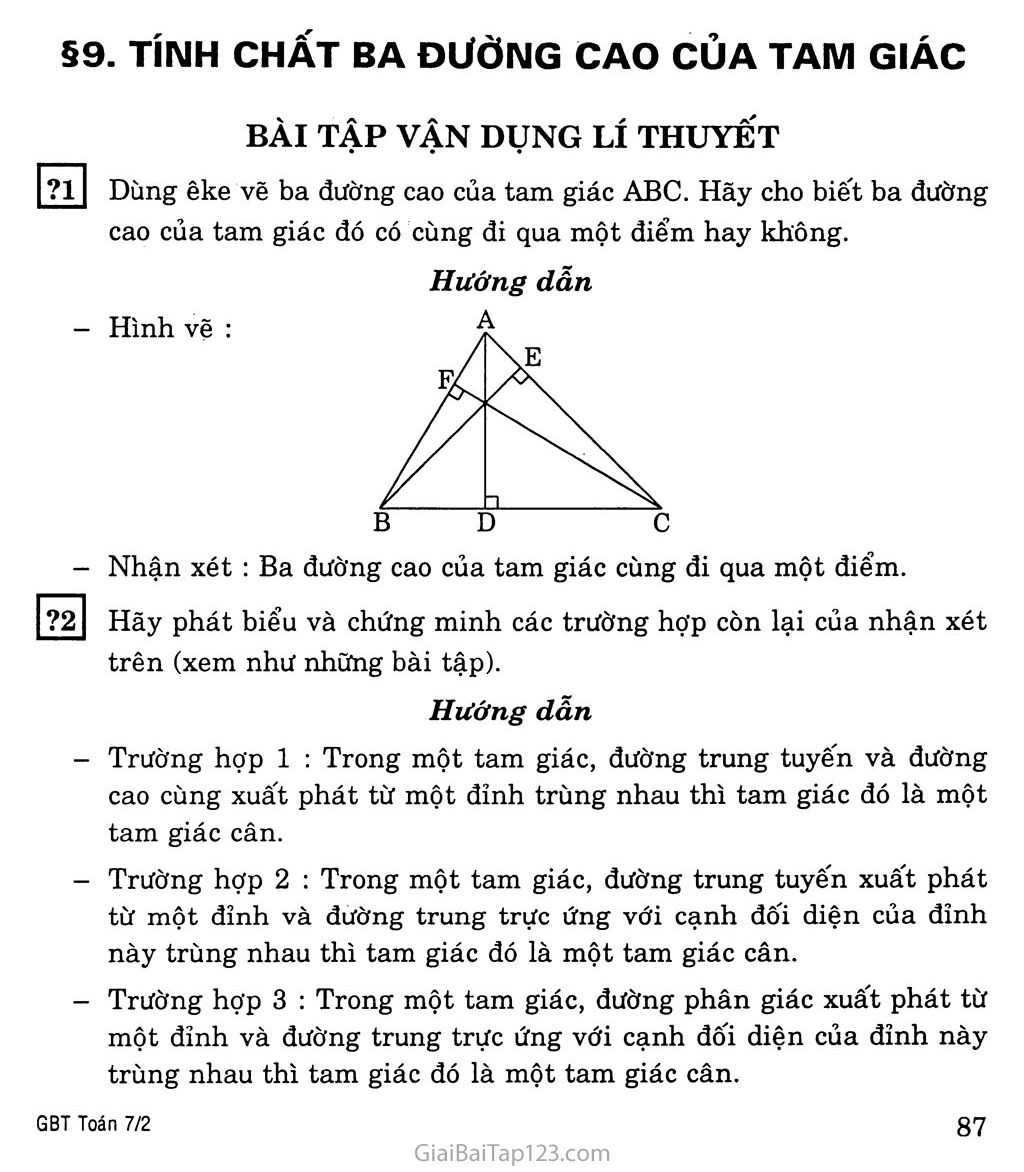
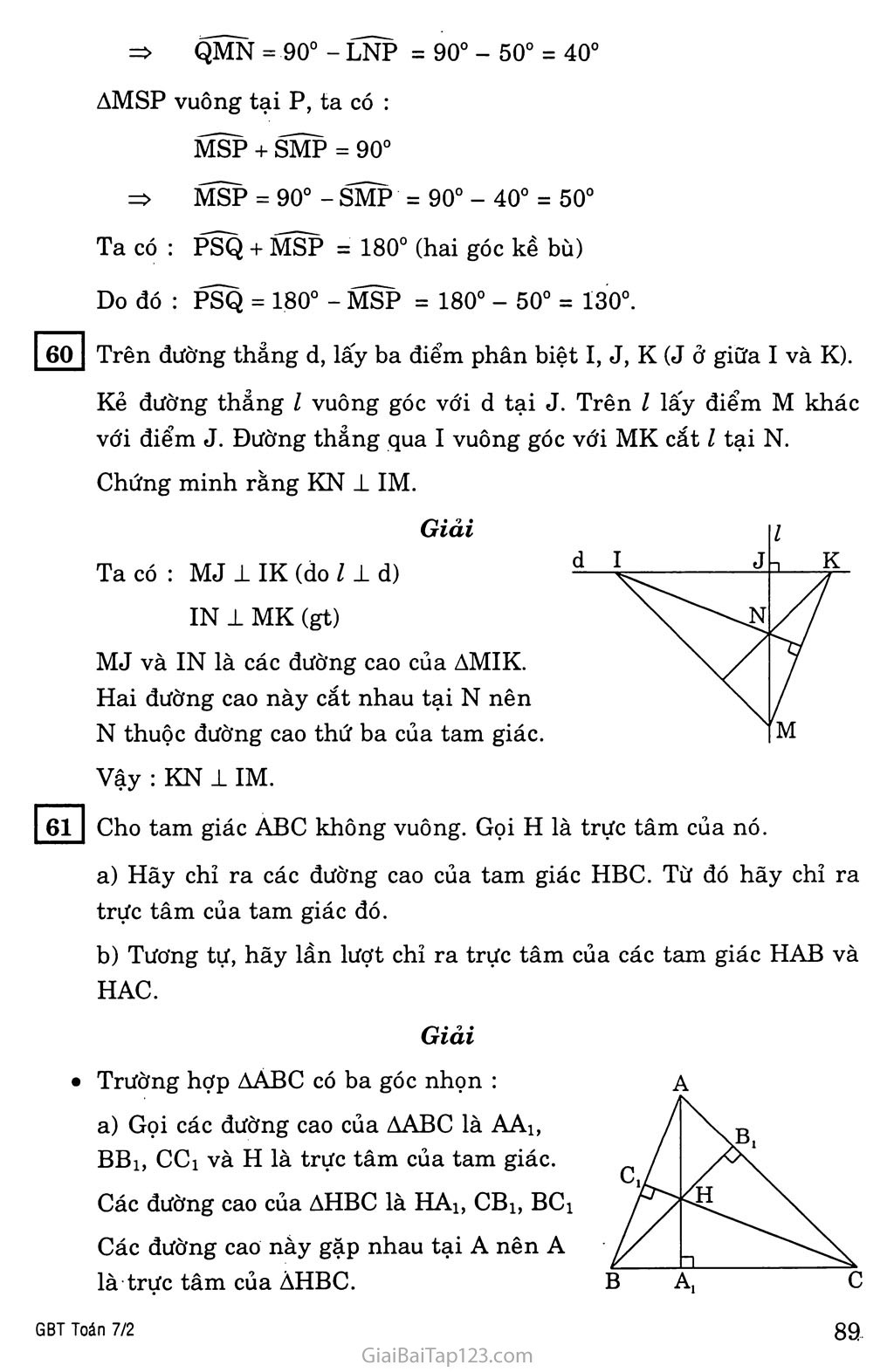
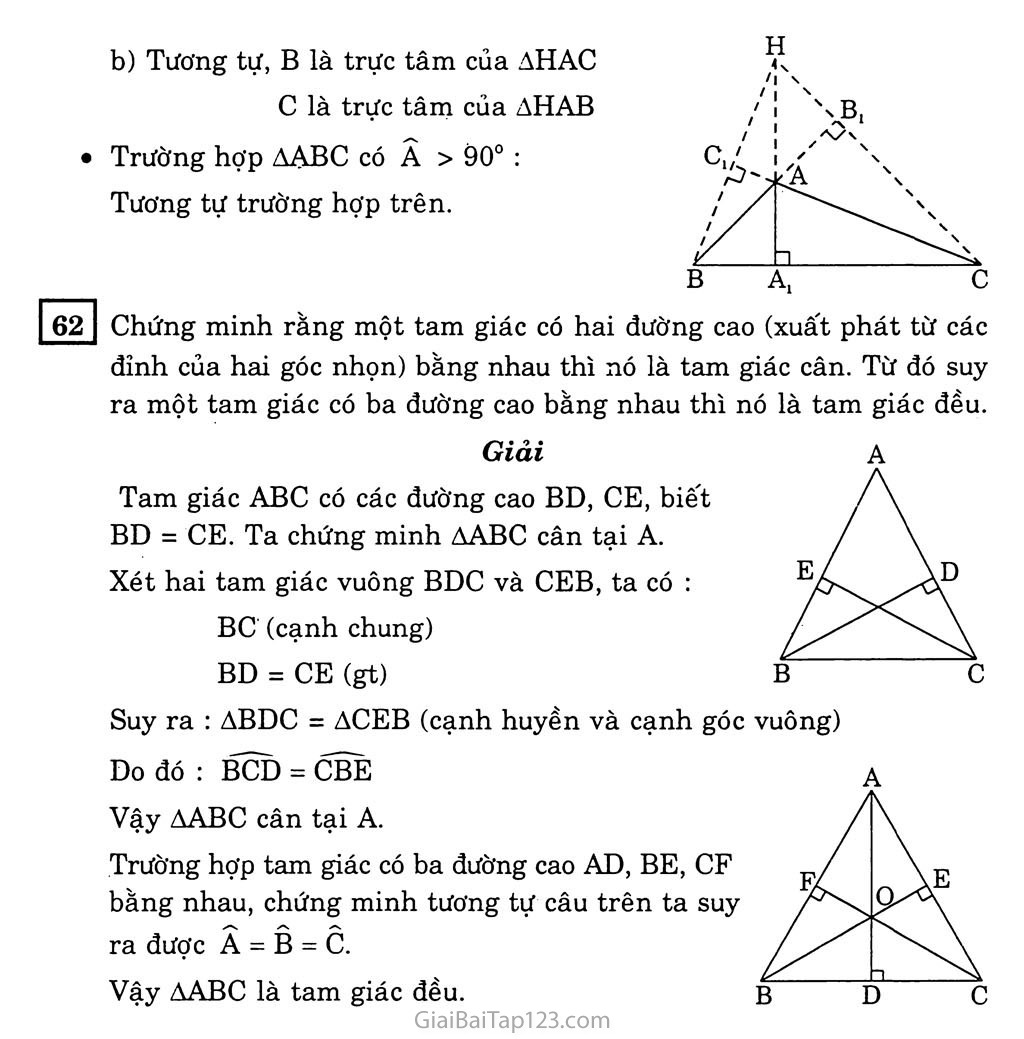
§9. TÍNH CHẤT BA ĐƯỜNG CAO CỦA TAM GIÁC
BÀI TẬP VẬN DỤNG LÍ THUYẾT
?1
Dùng êke vẽ ba đường cao của tam giác ABC. Hãy cho biết ba đường cao của tam giác đó có cùng đi qua một điểm hay không.
Hướng dẫn
- Hình vẽ :
Nhận xét : Ba đường cao của tam giác cùng đi qua một điểm.
?2
Hãy phát biểu và chứng minh các trường hợp còn lại của nhận xét trên (xem như những bài tập).
Hướng dẫn
Trường hợp 1 : Trong một tam giác, đường trung tuyến và đường cao cùng xuất phát từ một đỉnh trùng nhau thì tam giác đó là một tam giác cân.
Trường hợp 2 : Trong một tam giác, đường trung tuyến xuất phát từ một đỉnh và đường trung trực ứng với cạnh đối diện của đỉnh này trùng nhau thì tam giác đó là một tam giác cân.
Trường hợp 3 : Trong một tam giác, đường phân giác xuất phát từ một đỉnh và đường trung trực ứng với cạnh đối diện của đỉnh này trùng nhau thì tam giác đó là một tam giác cân.
LUYỆN TẬP
Hãy giải thích tại sao trực tâm của tam giác vuông trùng với đỉnh góc vuông và trực tâm của tam giác tù nằm ở bên ngoài tam giác.
Giải
Trường hợp tam giác vuông ABC (A = 90°)
Ta có BA, CA là đường cao xuất phát từ các đỉnh B, c và chúng gặp đường cao AI tại A. Vậy trực tâm của tam giác vuông trùng với đỉnh góc vuông.
Trường hợp tam giác tù ABC (A > 90°)
Ta có các đường cao BK, CL cắt nhau tại H. Trực tâm H không thể nằm trong tam giác hoặc trùng với điểm A.
Nếu H nằm trong tam giác thì khi đó các tam giác CAI và CAK có một góc vuông và một góc tù (điều này
không thể xảy ra vì tổng ba góc trong một tam giác là 180°).
Nếu H trùng với A thì AABC vuông tại A (trái giả thiết) Vậy trực tâm H nằm bên ngoài tam giác.
59
Cho hình bên.
Chứng minh NS ± LM.
Khi LNP = 50°, hãy tính góc MSP và góc PSQ.
Giải
a)
Ta có :
'MQ1LN
LP 1 MN MQ và LP là đường cao của AMLN
s là giao điểm của MQ và LP nên NS thuộc đường cao thứ ba của AMLN.
Vậy : NS ± LM.
b)
AMQN vuông tại Q, ta có :
L
M
p N
QMN + LNP = 90°
=> QMN = 90° - LNP = 90° - 50° = 40°
AMSP vuông tại p, ta CÓ :
MSP + SMP = 90°
=> MSP = 90° - SMP = 90° - 40° = 50°
Ta có : PSQ + MSP = 180° (hai góc kề bù)
Do đó : PSQ = 180° - MSP = 180° - 50° = 130°.
60 Trên đường thẳng d, lấy ba điểm phân biệt I, J, K (J ở giữa I và K).
Kẻ đường thẳng ỉ vuông góc với d tại J. Trên l lấy điểm M khác với điểm J. Đường thẳng qua I vuông góc với MK cắt l tại N.
Chứng minh rằng KN 1 IM.
Giải
Ta có : MJ 1 IK (do l 1 d)
IN 1 MK (gt)
MJ và IN là các đường cao của AMIK. Hai đường cao này cắt nhau tại N nên N thuộc đường cao thứ ba của tam giác.
Vậy : KN 1 IM.
61 Cho tam giác ABC không vuông. Gọi H là trực tâm của nó.
Hãy chỉ ra các đường cao của tam giác HBC. Từ đó hãy chỉ ra trực tâm của tam giác đó.
Tương tự, hãy lần lượt chỉ ra trực tâm của các tam giác HAB và HAC.
Giải
• Trường hợp AABC có ba góc nhọn :
Gọi các đường cao của AABC là AA1, BB1, CC1 và H là trực tâm của tam giác.
Các đường cao của AHBC là HAj, CB1, BC1 Các đường cao này gặp nhau tại A nên A là trực tâm của AHBC.
Tương tự, B là trực tâm của AHAC c là trực tâm của AHAB
Trường hợp AABC có A > 90° : Tương tự trường hợp trên.
62
Chứng minh rằng một tam giác có hai đường cao (xuất phát từ các đỉnh của hai góc nhọn) bằng nhau thì nó là tam giác cân. Từ đó suy ra một tam giác có ba đường cao bằng nhau thì nó là tam giác đều.
Giải
Tam giác ABC có các đường cao BD, CE, biết BD = CE. Ta chứng minh AABC cân tại A.
Xét hai tam giác vuông BDC và CEB, ta có :
BC (cạnh chung)
BD = CE (gt)
Suy ra : ABDC = ACEB (cạnh huyền và cạnh góc vuông)
Do đó : BCD = CBE
Vậy AABC cân tại A.
Trường hợp tam giác có ba đường cao AD, BE, CF bằng nhau, chứng minh tương tự câu trên ta suy ra được A = B = C.
Vậy AABC là tam giác đều.