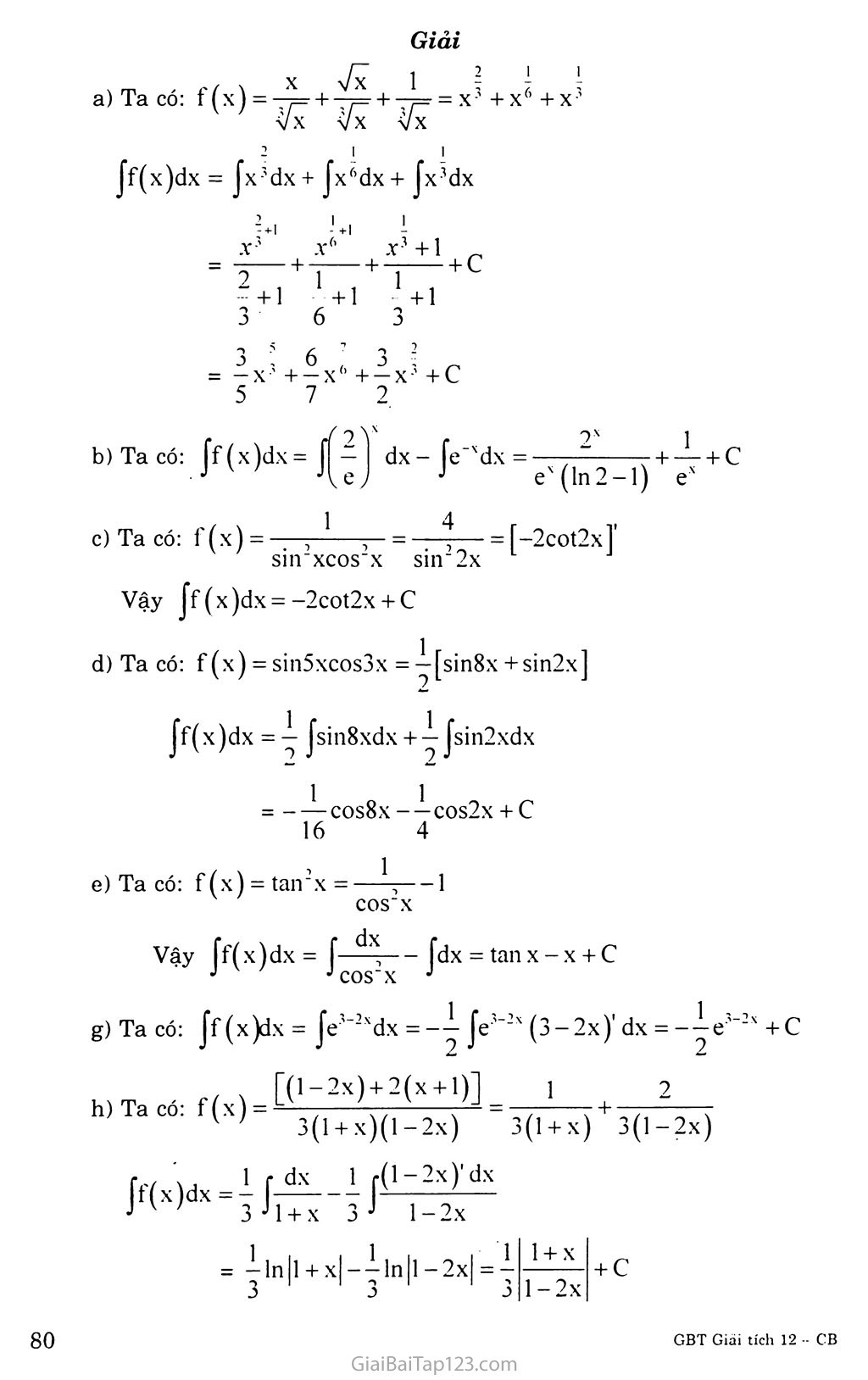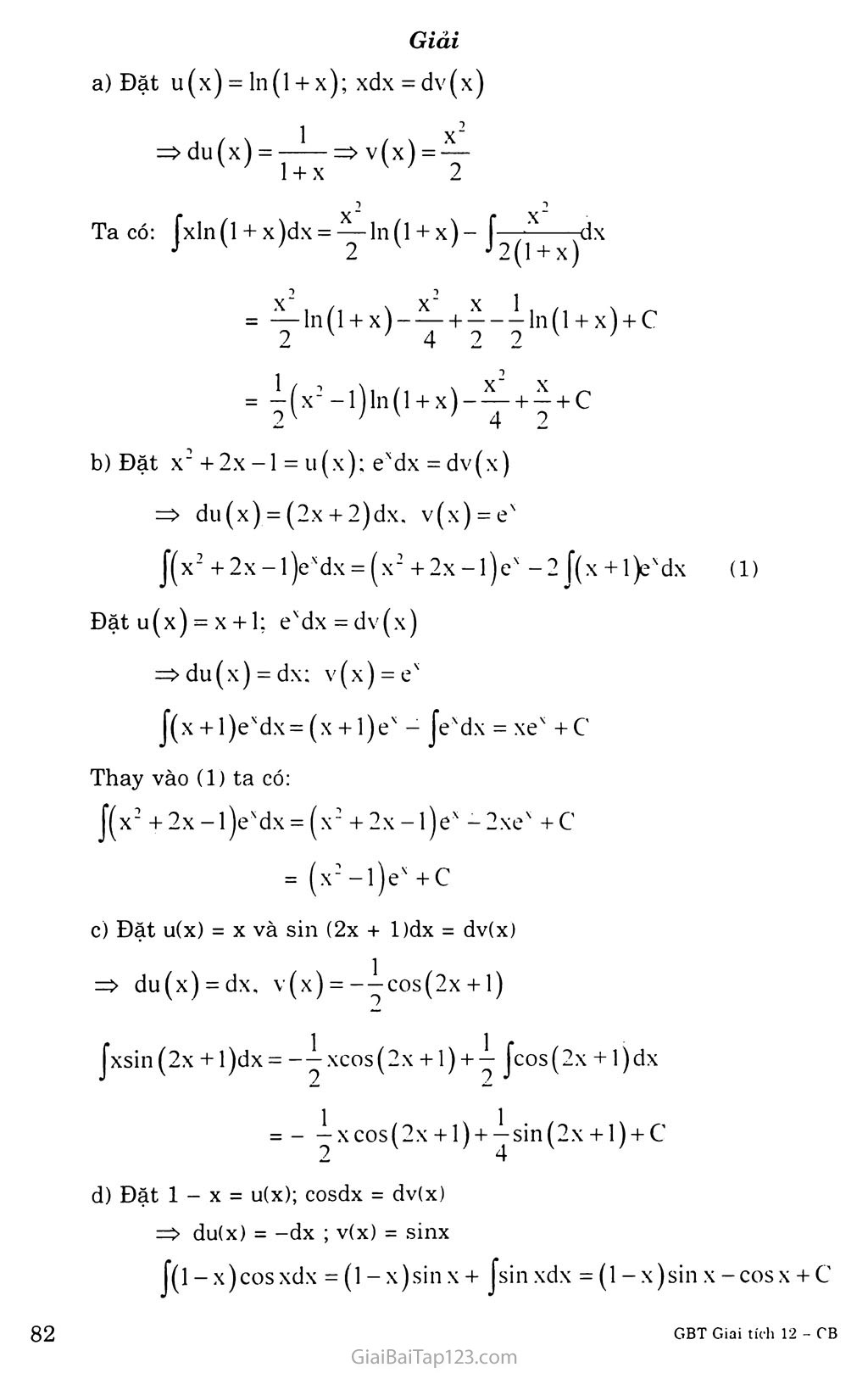Giải bài tập Toán 12 Bài 1. Nguyên hàm và tính chất

Chương III. NGUYÊN HÀM, TÍCH PHÂN VÀ ỨNG DỤNG
Bài 1. NGUYÊN HÀM VÀ TÍNH CHẤT
A. KIẾN THỨC CẦN NAM vững
Nguyên hàm
Cho hàm số’ f(x) xác định trên K (K là nửa khoảng hay đoạn của trục số). Hàm số F(x) được gọi là nguyên hàm của hàm sô' f(x) trên K nếu F’(x) = f(x) với mọi X thuộc K.
Định lí: Nêu F(x) là một nguyên hàm của hàm sô' f(x) trên K thì:
Với mỗi hằng sô' c, F(x) + c cũng là một nguyên hàm của hàm sô' f(x) trên K.
G(x) cũng là một nguyên hàm của hàm sô' f(x) trên K thì tồn tại một hằng sô' c sao cho G(x) = F(x) + c.
Tính chất
^Jf(x)dx^j = f(x) và Jf’(x)dx = f(x) + c
Jkf(x)dx = k jf(x)dx (k là hằng số)
J[f(x)±g(x)] dx= Jf(x)dx ± Jg(x)dx
Bảng nguyên hàm
Jodx = c	Jdx=x + C
fx“dx = —ỉ—x“+l+c (a£-1)	[—dx = ln|x| + c
J a+1	Jx 11
fexdx = ex+c	faxdx = -^—+ c (a>0; a*l)
Jcosxdx = sin x+ c	Jsinxdx =-cosx+ c
ị—Ỉ5— dx = tan X + c	í dx = - cot X + c
JCOSJX	Jsin X
Phương pháp tính nguyên hàm
* Đổi biến số:
Nếu Jf(u)du = F(u) + c và u(x) là hàm sô' có đạo hàm liên tục thì:
Jf(ux)u’(x)dx = F(u(x)) + c
* Tính nguyên hàm từng phần:
Nêu hai hàm sô u = u(x) và V = v(x) có đạo hàm liên tục trên K thì:
Ju(x)v'(x)dx = u(x)v(x)- ív(x)u'(x)dx
hay
Judv = uv- Jvdu.
B. GIẢI BÀI TẬP
Trong các cặp hàm số’ dưới đây, hàm sỏ’ nào là nguyên hàm của hàm sô’ còn lại?
e‘x và-e"x	b) sin2x và sin2 x
f	2Ỹ x x <	4V
c) 1 — e và 1 —- ex
V	X 7	<	X)
Giải
Ta có: x J = -e x. Vậy e x là nguyên hàm của -e x
Ta có: [_sin2 xl - 2sin xcosx =sin2x . Vậy sin2 X là nguyên hàm của sin2x.
Ta có:
ex
2 V
ex.
í , 4 , x	,
Vậy 1—■ |e là nguyên hàm của hàm sô 1	
1 X
Tìm nguyên hàm của các hàm sô’ sau:
a)
b)
c)
sin xcos X
d)
g)
g)
Giải
a) Ta có
VX
Ta có: [f(x)dx = [í-ì dx- [e Xdx =	—— + -Ỉ- + C
J	J ex(ln2-l) ex
Ta có: f (x) = ■; , —ỵ— =	- [-2cot2xĩ
sin xcos X sin 2x
Vậy if (x)dx =-2cot2x+ c
Ta có
- — cos8x -—cos2x 4- c
16	4
e) Ta có
g) Ta có:
•> 1
Jf (x)dx = Je’ 2xdx = -y Je3 2x (3-2x)' dx = -^-e' 2x +c
h) Ta có:
(l + x)(l-2x)
1	2
f(x) =
r(l-2x)'dx
3J l-2x
Sử dụng phương pháp đổi biển số, hay tính:
J(1-x) dx (đặt u = 1 - x)
Jx(l + x2pdx (đặt u = 1 + X2)
[cos’xsinxdx (đặt t = cosx)
d) [————— (đặt u = ex + 1) Je + e x+2
Giải
Đặt u = 1 - x; du = - dx
Vậy [(1-x)) dx = - iuQdu =+ c =--—-- ) - + c
Đặt X2+2x-l = u(x); exdx = dv(x)
=> du(x) = (2x + 2)dx, v(x) = ex
J(x2 +2x-l)exdx = (x2 + 2x-l)ex -2 [(x + l)exdx (1)
Đặtu(x) = x + 1; exdx=dv(x)
=>du(x) = dx; v(x) = ex
J(x + l)exdx=(x + l)ex - |exdx = xex +c
Thay vào (1) ta có:
j(x2 + 2x -l)exdx = (x2 + 2x -l)ex - 2xex + c
= (x2-l)ex+c
Đặt u(x) = X và sin (2x + l)dx = dv(x) => du(x) = dx, v(x) = --^-cos(2x +1)
Jxsin (2x + l)d
(2x + 1) + ^- Jcos(2x + l)dx
1
x = xcos
2
Đặt 1 - X = u(x); cosdx = dv(x)
=> du(x) = -dx ; v(x) = sinx
1 - x)cos xdx = (1 - x)sin X + Ị sin xdx = (1 - x)sin X -cosx + c