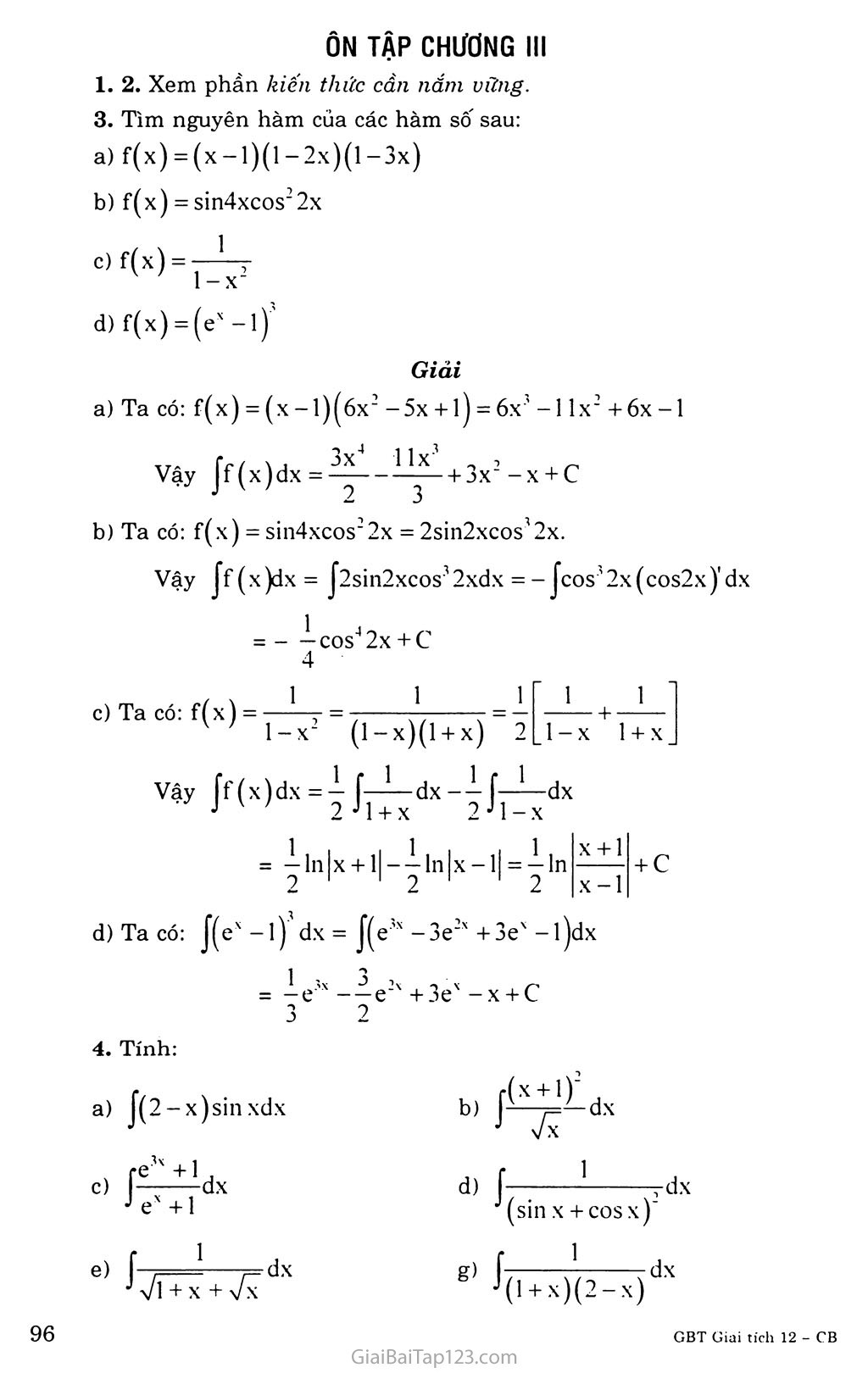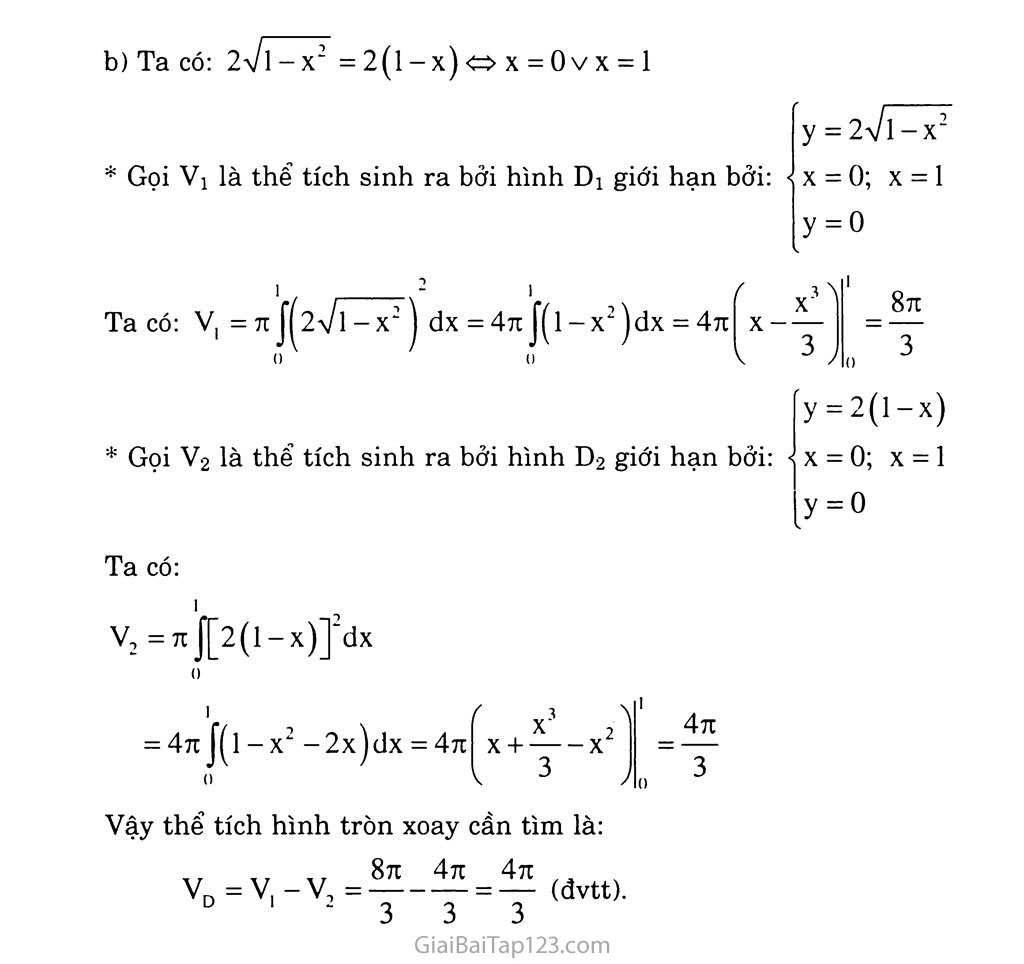Giải bài tập Toán 12 ÔN TẬP CHƯƠNG III

ÔN TẬP CHƯƠNG III
1. 2. Xem phần kiến thức cần nắm vững.
Tìm nguyên hàm của các hàm sô' sau:
f(x) = (x-l)(l-2x)(l-3x)
f(x) = sin4xcos22x
f(x)=7Z^
f(x) = (ex -1)
Giải
Ta có: f(x) = (x-l)(óx2 -5x + 1) = 6x‘ -1 lx2 +6x-1
Vậy Jf(x)dx = ^|—^-y- + 3x2-x + c
Ta có: f(x) = sin4xcos22x = 2sin2xcos;2x.
Vậy Jf(x)dx = |2sin2xcos?2xdx = - Jcos;'2x(cos2x)'dx
= - — cos Tính:
2x + c
4
c) Ta có: f(x) =
Vậy [f(x)dx = ^- f—— dx-ị í—— dx
J '	2 J1 + X 2 J1 - X
d) Ta có: í(ex -l)'dx = J(e,x -3e2x +3ex -l)dx
= ịe;" -4e2x +3ex -x + c
3	2
a) |(2-x)sinxdx
e) f	dx
J V1 + X + 7x
d) Ỉ7T	^dx
J (sin X + COS x)
g) Ta có:
Giải
Đặt u = 2 - x; sinxdx = dv du = -dx; V = -cosx
2-x)sinxdx = (x-2)cosx- Ịcosxdx
- (x-2)cosx-sinx + C.
b) Đặt u = (x + l)2;dv = -^t=>du = 2(x + l)dx; v = 2a/x
x/x
Vậy [—	-t-	-dx=t [——dx + ị J—Ị— dx
■ -I(1 + x)(2-x)	3J2-X	3-H + x
= ịln|l + x|-ịln|2-x|=ị^^
3	3	3 2 - X
5. Tính:
a' í-^=dx
0JVl + x
Jx2e3xdx
0
d) JVl + sin2xdx
0
Giải
a) Đặt l + x = u=>x = u- l;
X - 3 => u = 4; du = dx
X = 0 => u = 1
Jx2e3xdx = ị Jx2d(e3x) = ^x2e3x Jxe’"dx 0	■’í	-5	0 J 0
26eô-2
27
d) Ta có:
|Vl + sin2x dx= Jvsin2 x + cos2 x + 2sinxcosx dx 0
= V2 jcos dx-V2 Jcos x-^ dx
0 V 4 J	V 4)
6. Tính:
n
2
a) Jcos2xsin2xdx
0
I
b) J|2x-2’x|dx -1
C) ;f(x + 1)(x + 2)(x + 3),
r	X2
dx
d)
I ,	dx
0 X2 — 2x —3
ĨĨ
g)
Giải
a) Ta CÓ: cos2sin2 x =—cos
2
2x(l -cos2x) = _ cos2x— _ cos4x- — v ’ 2	4	4
7t	71
2
Vậy Jcos2xsin2 xdx =-
0	0
Ị 2	Ị 2
jcos 2xdx - J Jcos 4xdx -
2 0	4 0
— sin2x sin4x - —X
4	16
b) Ta CÓ: |2X -2 x| =
c) Ta CÓ:
d) Ta CÓ:
^x2 -2x-3
2X - 2 x với
2 x - 2X với
.X
11 6 , A .
x + —+ A + 6 dx X X )
4 +11 In X - — + 6x
2
ax ' |	' •
4 ? X - 3	-r ..
T- 5 A J	-r 0
_rfj_dx=iln
4„JX + 1	4
1 _J_
0 - ln2
= ^ + llln2
2
x-3
-ịln3
2
71
2
=4 + 1
2
g) Ta có: J(x + sinx)2 dx = |(x2 + 2xsinx + sin2 x)dx ()	0
X' X	1
— + —-2xcosx + 2sinx - — sin2x
3 2	4
71
' 0
Xét hình phẳng D giới hạn bởi y = 2-ựl -X2 và y = 2(1 - x)
Tính diện tích hình D
Quay hình D xung quanh trục Ox. Tính thể tích khối tròn xoay được tạo thành.
Giải
a) Ta CÓ
Vậy tích hình D là:
I
s= J[2ựl-x2-2(l-x)]dx
()
-x2dx-2 X —-3—
2
Đặt I = 21\/1 - x2dx , ta CÓ: s = I - 1 I)
* Tính I:
Đặt X = sint => dx = costdt
Ta có: X = 0 => t = 0
71
2
2	
Vậy I = 2 JV1-sin21 costdt
()
1
t + ^-sin2t
2
Vậy s = I -1 => s = y -1 (đvdt)
Ta có: 2-ựl-x2 = 2(1 - x) « X = 0 V X = 1
* Gọi Vi là thể tích sinh ra bởi hình D1 giới hạn bởi:
Ta có: V, = 7T |^2>/1 -X2) dx
()
1
= 471 |(l-x2)dx = 471
(I
* Gọi v2 là thể tích sinh ra bởi hình D2 giới hạn bởi:
Ta có:
1
V2 = 71 J[2(l-x)]?dx
0
1
= 4n J(1 - X2
()
-2x)dx = 471
a.2Ẻ_v2
X + -—-X
l 3
471
3
y = 2Vl-x2
X = 0; X = 1
8n
3
y = 2(l-x)
■ x = 0; X = 1
y = 0
Vậy thể tích hình tròn xoay cần tìm là:
w w 871 471	47t, . _
VD=V|-V2=y-y = y (đvtt).