Giải bài tập Toán 12 Bài 2. Cực trị của hàm số

Bài 2. cực TRỊ CỦA HÀM số
A. KIẾN THỨC CẦN NAM VỮNG
Định nghĩa cực trị
Cho hàm số y = f(x) xác định và liên tục trên khoảng (a; b) và điểm Xo e (a; b).
- Nếu có số’ h > 0 sao cho Xo e (a; b), (x0 - h; Xo + h) C2 (a; b) ta có fix) < flx0) V xe (x0 - h; Xo + h), X Xo thì khi đó Hx) đạt cực đại tại Xo và f(x0) là giá trị cực đại của hàm số’ fix).
10	GBT Giải tích 12 - CB
Nêu có số h > 0 sao cho Xo e (a; b), (x0 - h; Xo + h) c (a; b) ta có f(x) > f(x0) V X G (x0 - h; Xo + h), X Xo thì khi đó fix) đạt cực tiểu tại Xo và f(x0) là giá trị cực tiếu của hàm sô' f(x).
Cực đại hay cực tiểu của f(x) gọi chung là cực trị của fix).
Điều kiện để hàm sô có cực trị
Định lí 1: Cho hàm sô' y = fix) liên tục trên K = (xo - h; Xo + h), h > 0 và có đạo hàm trên K hoặc trên K \ {xol, nếu:
f(x) > 0 trên (x0 - h; Xo) và f(x) < 0 trên (x0; Xo + h) thì Xo là một điểm cực đại của fix).
f(x) 0 trên (x0; Xo + h) thì Xo là một điểm cực tiểu của fix).
Định lí 2: Cho hàm sô' y = fix) có đạo hàm cấp hai trong khoảng (x0 - h; Xo + h) với h > 0. Nếu:
f(xo) = 0; f’(x0) > 0 thì Xo là điểm cực tiểu.
—F(xq) = 0; f’(x0) < 0 thì Xo là điểm cực đại.
Tìm cực trị
Quy tắc 1: Ta có thế’ tìm cực trị của hàm sô' y = fix) như sau:
Tìm tập xác định của hàm sô' rồi tính fix).
Tìm các điểm mà tại đó f(x) không xác định hoặc bằng không.
Lập bảng biến thiên.
Từ bảng biến thiên suy ra các điểm cực trị.
Quy tắc 2: Ta có thể tìm cực trị của hàm sô' y = fix) như sau:
Tìm tập xác định của hàm số rồi tính f(x).
Giải phương trình f(x) = 0 và kí hiệu Xi (i = 1, 2, 3, ...) là các nghiệm của nó.
Tính f’(x) và f’(Xi).
Dựa vào dâ'u của f’(xi) suy ra tính chất cực trị của điểm Xi.
B. GIẢI BÀI TẬP
Áp đụng Quỉ tắc 1, hãy tìm các điểm cực trị của các hàm số sau:
y = 2x3 + 3x2 -36x - 10 b) y = X4 + 2x2 - 3
y = X + —	d) y = X3 (1 -x)2
X
y = Vx2 — x + 1
Giải
Ta có: D = R
y’ = 6x2 + 6x - 36 = 6(x2 + X - 6)= 0
 X = - 3 hoặc X = 2
Bảng biến thiên:
Hàm số đạt cực đại tại X = -3 và đạt cực tiểu tại X = 2, vậy đồ thị của hàm số có điểm cực đại là (-3; 71) và điểm cực tiểu là (2; -54).
Ta có: D = R
y’ - 4x3 + 4x = 4x (x2 + 1) = 0 X - 0
Bảng biến thiên:
Vậy hàm sô' có điểm cực tiểu là X = 0.
Ta có: D = R \ Ịo}
y' = 1	y = 0 o X = ± 1, hàm số không xác định tại X = 0
X
Bảng biến thiên:
Ta có: D = R
y’ = 3x2 (1 - X)2 -2x3(1 - x) = X2 (5x2 - 8 X + 3) = 0 3
 x = 0;x=l;x= —
5
Bảng biến thiên:
Ta có: X = 0 không phải là điếm cực trị vì tại điểm đó đạo hàm bằng 0 nhưng đạo hàm không đổi dấu khi X đi qua X = 0.
-> 0 Vx G R 4
e) Ta có: X2 - X + 1 =
Do đó, với mọi X e R thì 7.X2 -x + 1 luôn luôn xác định. Vậy D - R.
2x-l „ . .	1
= 0 x = -2
2a/x2 -X +1
Bảng biến thiên:
2
b) y = sin2x - X
d) y = X5 - X3 - 2x + 1 Giải
Áp dụng Qui tắc 2, hãy tìm các điếm cực trị của các hàm sô sau:
y = X4 - 2x2 + 1 c) y - sinx + cosx
a) Ta có: D = R
y’ = 4x3 - 4x = 0 X = 0, X = ± 1
y” = 12x2 - 4
y”(0) = -1 0=>x = -lvàx=llà các điểm cực tiểu.
Ta có: D = R
.71
y = 2cos2x - 1 = 0 X = ± -7 + k7t, k e z
6
y” = -4sin2x
y —+ K71 =-4sin-- xrn=-- + k7i,kG z <6	)	3 CD 6
y --? + k7i = 4sin_ > 0 => xrT= - -7 + k7T,k e z I 6 J 3 CT 6
Ta có: D = R
. 	.. nz .(.. , 71A
y = sinx + cosx => y = <2 sin X + — k 4 J
y' = Vicos X+-Ị ,y' = 0 X = Ị + k7T, keZ
I 4j	4
, 71Ì
y = -s/2 sin X + —
I 4J
m	,/7t ,	/- . (71 , ị -VI nếu k chan
Ta CÓ: y — + k7T =-V2 sin ;-+k7T = < _
V 4 J <2 J VI nếu k lẻ
Vậy hàm sô đạt cực đại tại điểm x=-y + 2k7T và cực tiểu tại điểm
4
x=^ + (2k + l)7i,VkeZ.
Ta có: D = R
y’ = 5x4 - 3x2 - 2 = 0 X = ± 1 y” = 20x3 - 6x
ỹ”(-l) = -20 + 6 = -14 XCĐ = -1
ỹ”(l) = 20 - 6 = 14 > 0 => XCT = 1
Chứng minh rằng hàm sô' y = ựjx| không có đạo hàm tại X = 0 nhưng vẫn đạt cực tiểu tại điểm đó.
Giải
Ta có, giới hạn của tỉ sô' ~ thuộc hàm sô' y = Vjlĩ tại Xo = 0 là: Ax	VI I •
Av	\l 0 + Ax - VÕ a/Ax
lim = lim 	—	= lim ^-2-
Ax->0 Ax Ax->() Ax	Ax
|Ax| [-00 với Ax < 0
= lim— 21— = -
Ax“‘" Axự|Ax| [+ot với Ax < 0
Nghĩa là hàm số y = ự|x| không có đạo hàm tại X = 0.
Xét y - trong khoảng (0 - h; 0 + h) với h > 0, ta có: 7ịxj>0, Vxe(o-h; 0 + h); x*0
Vậy hàm số y = ựjx| đạt cực tiểu tại X = 0.
Chứng minh rằng với mọi giá trị của tham số m, hàm số y = X3 - mx
X- —
 a
 - 2x + 1 luôn luôn có một điểm cực đại và một điểm cực tiểu.
Giải
Xét hàm số’ y = X3 - mx2 - 2x + 1, ta có:
D = R
y' = 3x2 -2mx-2 = 0
m - Vin2 +6 m + Vm2 +6
 X. =	4-	V X, =	4-	
1	3	2	3
Với mọi giá trị của m ta đều có X1 < 0 < X2.
Bảng biến thiên:
Qua bảng biến thiên ta thấy hàm sô’ đã cho có XCĐ =	4	 và
m +Vm2 +6 	 ,	.
X™. =	—	 với mọi giá trị cua tham số m.
c 3
Tìm a và b đế các cực trị của hàm sô’ y - ~-a2x3 + 2ax2 -9x + b đều là những sô’ dương và x() = “ là điểm cực đại.
Giải
Ta có: Nếu a = 0 thì y = -9x + b. Vậy hàm số không có cực trị. Nếu a * 0. Khi đó:
9
y' = 5a2x2 +2ax-9; y' = 0
X = ------
5a
Ta xét hai trường hợp:
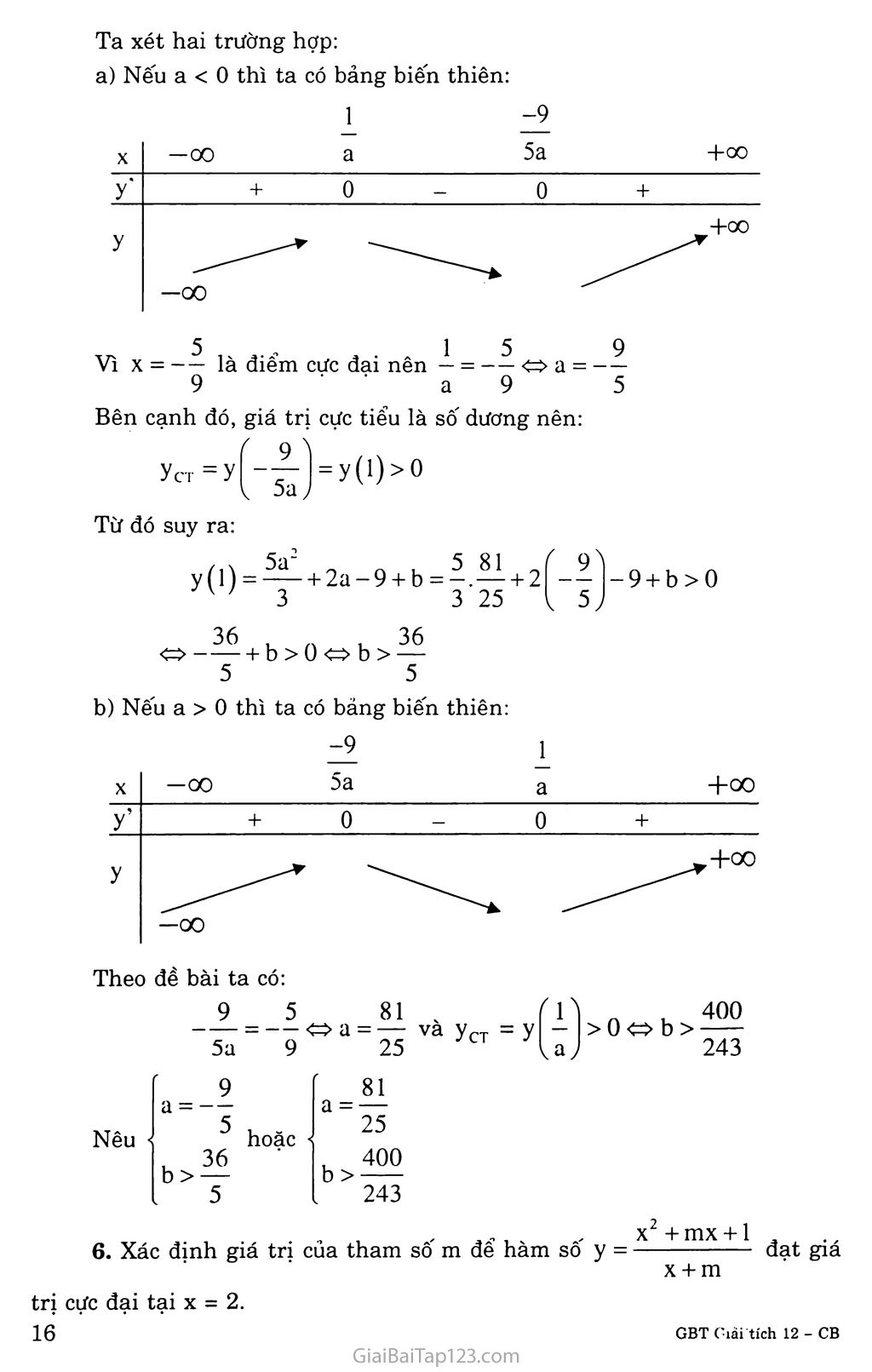
a) Nếu a < 0 thì ta có bảng biến thiên:
X
1 ~	Xác định giá trị của tham sô' m để hàm sô' y =	—	 đạt giá
 X + m
 trị cực đại tại X = 2.
 16
—00	a	5a	+co
y'
+	0	—	0	+
y
+00
—00
Vì X = -7- là điểm cực đại nên — =	 a =
9	a 9	5
Bên cạnh đó, giá trị cực tiểu là sô' dương nên:
Từ đó suy ra:
y(l) = ^l + 2a-9 + b = |.-^ + 2f-|ì-9 + b>0
v ’	3	3 25 V 5 J
36 , n , 36
--7-+ b > 0 b >-7-
5	5
Nếu a > 0 thì ta có bảng biến thiên:
Giãi
Ta có: D = R \ l-m}
X2 + 2mx + m2 -1
(x + m)
y’ = 0 X, = -m -1 V X, = -m + 1
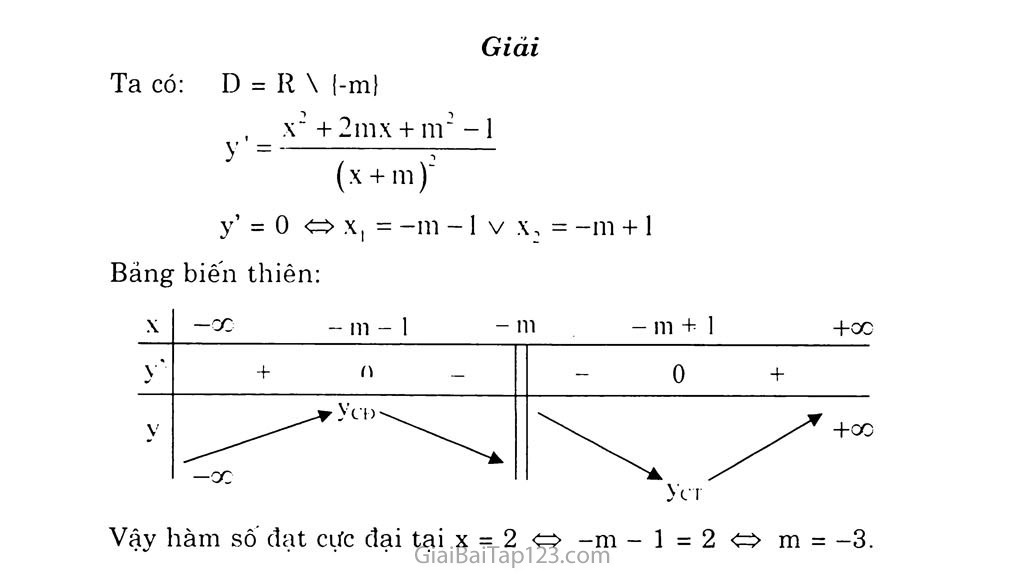
Bảng biến thiên:
Vậy hàm sô' đạt cực đại tại X = 2 -m -1 = 2« m = -3.