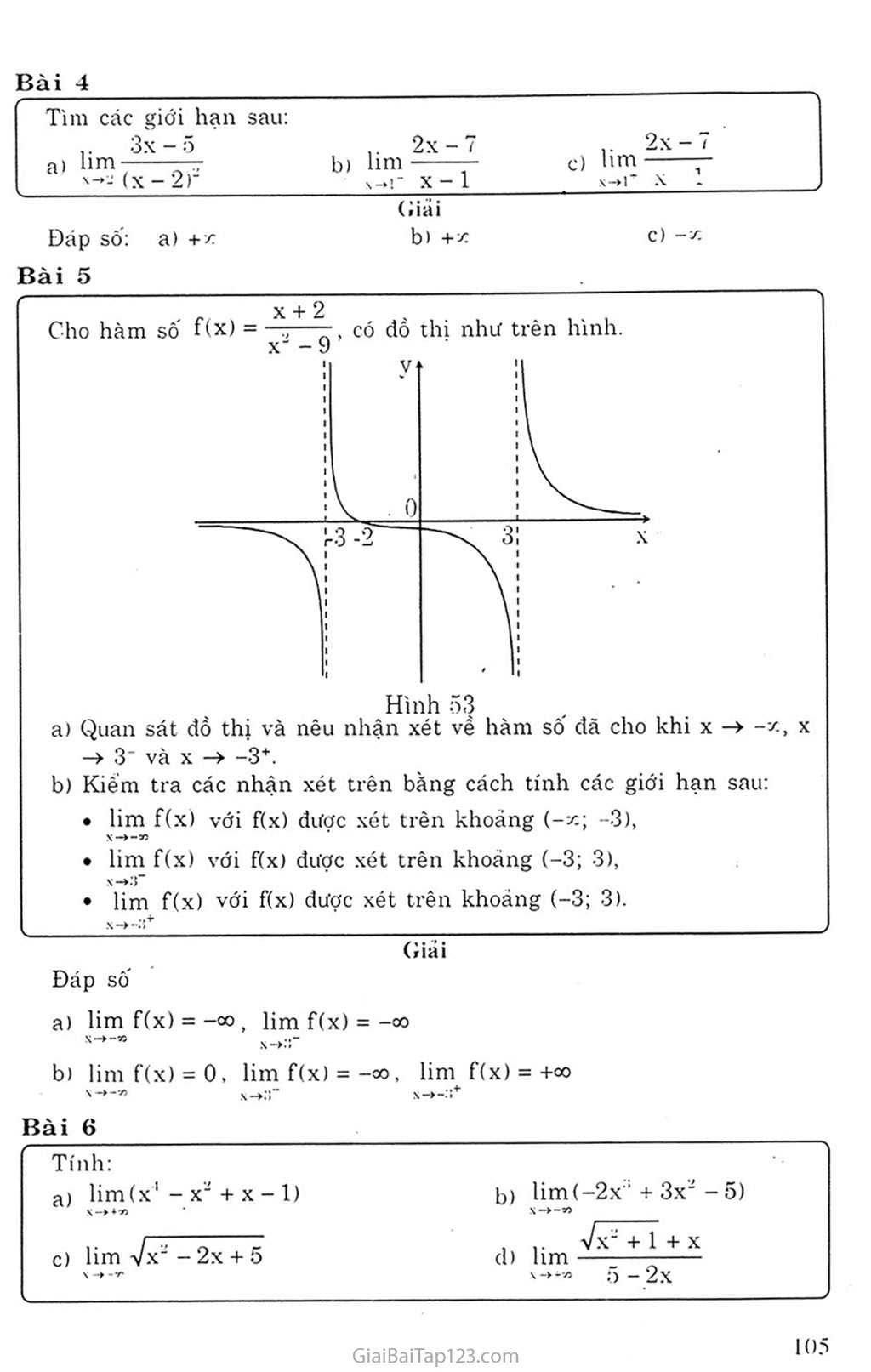
Giải Toán 11: Vấn đề 2. Giới hạn của hàm số

VẤN ĐỂ 2. GIỚI HẠN CỦA HÀM số
A. Kiên thức cần nhớ
Giới hạn hữu hạn của hàm sô' tại một điểm
Định nghĩa Định nghĩa 1
Cho khoảng K chứa điểm x0 và hàm số y - f(x) xác định trên K hoặc trên K \ (x0|.
Ta nói hàm sô' y = f(x) có giới hạn là số L khi X dần tới x0 nếu với dãy sô' (xn) bất kì, xn e K \ (xq( và xn -» X(j, ta có f(xn) -> L.
Kí hiệu lim f(x) = L hay f(x) —> L khi X -> xn.
X-»X(|	u
Định lí về giời hạn hữu hạn Định lí 1
Giá sứ lim f(x) - L và lim g(x) = M . Khi đó
x-»x„	X—>xo
lim [f(x) + g(x)] = L + M ;
lim [f(x) - g(x)] = L - M ;
lim [f(x).g(x)l = L.M ;
.. f(x) L
lim	 = —- (nêu M * 0)
X-K, g(x) M
Nếu f(x) > 0 và lim f(x) = L, thì
x->x„
L > 0 và lim ựf(x) = VẼ
x-»x,,
(Dâ'u của f(x) được xét trên khoảng đang tìm giới hạn, với X x0)
Giới hạn một bên Định nghĩa 2
Cho hàm số y - f(x) xác định trên khoáng (x0; b).
Số L được gọi là giới hạn bên phải của hàm số y = f(x) khi X —> x0 nếu với dãy số (xn) bất kì, x0 < xn < b và xn -» x0, ta có f(xn) -» L.
Kí hiệu: lim f(x) = L
%x_>x0A,
Cho hàm so y = f(x) xác định trên khoảng (a; x0).
Số L được gọi là giới hạn bèn trái của hàm sô y = f(x) khi X —> x0 nếu với dãy số (xn) bất kì, a L.
Ki hiệu: lim f(x) = L
.\->x 0
Định lí 2
lim f(x) = L khi và chi khi lim f(x) = lim f(x) = L. x->x„	x->xõ	X_>XO
Giới hạn hữu hạn của hàm sô' tại vô cực Định nghĩa 3
Cho hàm sô' y = f(x) xác định trên khoảng (a; +x).
Ta nói hàm số y - f(x) có giới hạn là sô L khi X -> +x nếu với dãy sô (xn) bất kì, xn > a và Xn —> +x, ta có f(xn) -» L.
Kí hiệu: lim f(x) = L hay f(x) -> L khi x -» +-S-.
X-»+£O
Cho hàm sô' y = f(x) xác định trên khoảng (-x; a).
Ta nói hàm số y = f(x) có giới hạn là sô L khi X —> -X nếu với dãy sô (xn) bất kì, xn -X, ta có f(xn) —» L.
Kí hiệu: lim f(x) = L hay f(x) -> L khi X —» -X.
X—»-»
Giới hạn vô cực của hàm sô'
Giới hạn vô cực
Định nghĩa 4
Cho hàm sô' y = f(x) xác định trên khoảng (a; +x).
Ta nói hàm sô' y = f(x) có giới hạn là -X khi X -> +x nếu với dãy sô'
(xn) bất kì, Xn > a và xn —> + x, ta có f(xn) -> -X.
Kí hiệu: lim f(x) = -00 hay f(x) -> -X khi fx -> +x.
X—>+w
Nhận xét:
lim f(x) =+00 lim(-f(x)) = -00
X—>+00	X—>+«
Một vài giới hạn đặc biệt
lim xk = +00 với k nguyên dương.
lim xk = -00 nếu k là sô lẻ.
x->-»
lim xk = +00 nếu k là số chẵn.
X—>—30
Một vài quy tắc về giới hạn vô cực
Quy tắc tìm giới hạn của tích f(x).g(x)
Nếu lim f(x) = L * 0 và lim g(x) = +00 (hoặc -x) thì lim f(x)g(x) được
, ,	,	x->x„	'
tính theo quy tăc cho trong bang sau:	
lim f(x)
x->x0
lim g(x)
x->x0
lim f(x)g(x)
x->x0
L > 0
+CO
+CO
-CO
-co
L < 0
+CO
-co
-CO
+00
b) Quy tắc tìm giới hạn của thương —-— g(x)
lim f(x)
x->x0
lim g(x)
x->x0
Dâu của g x)
,. f(x) lim ■ x-*x0. g(x)
L
+CO
Tùy ý
0
L > 0
0
+
+ 30
-
-CO
L < 0
+
-co
-
+CO
B. Giải bài tập sách giáo khoa
Bài 1
2 - 5x'2 X2 + 3
Dùng định nghĩa, tìm các giới hạn sau:
lim——-	•	b) lim
X-»| 3x — 2
a) Hàm sò
f(x) =
x + 1
3x - 2 2
xác định tròn
u I 3 ;+c0 I và X ■= 4 e
,	. „	(2 Ì
Giả sử (xn) là dãy so bat ki, xn e 1 3 ’ +0° h xn
; +°° I; x„ 4 và xu -> 4 khi n -> +x.
x +1	4+1	1
Ta CÓ lim f(xn) = lim ' 11	L = 4
"	3xn - 2	12-2	2
x + 1	1
Vậy lim _
X “i 3x - 2	2	_ „
2 - 5x2
b) Hàm số f(x) = —„	xác định trên R.
X + 3
Giả sử (x, ) là dãy số bất kì, X -» +30 khi n -» +30.
X-5
2 - 5x2	X2
Ta có limf(x ) = lim " = lim n = -5.
4+3	1+3
.	2-5x2 c	x"
Vậy lim —;—-- = -5.
Bài 2
X-++CO X + 3
Cho hàm số f(x) =
Vx + 1 nếu X > 0 2x nếu X < 0
và các dãy số (u ) với u = — , (v ) với vn = - —.
n	n
Tính lim un, lim vn, lim f(un) và lim f(vn).
Từ đó có kết luận gì về giới hạn của hàm số đã cho khi X
0?
Giải
Ta có: lim un = lim — = 0 ; lim vn = lim I - — I = 0.
n	\ nJ
Do u = — > 0 và vn = — — < 0, nên f(u ) - J—I n	, n .	V n
‘	( /1.4 ,	- n
Từ đó: limf(un) = lim J— + 1 = 1; lim f(vn) = lim—= 0.
Vn
+ 1 và f(vn) =
n
-2
V ’	)
Vì un -> 0 và vn —> 0, nhưng lim f(un) + lim f(vn) nên hàm số y = f(x) không có giới hạn khi X -> 0.
Bài 3
Tính các giới hạn sau: X2 -1
a) lim-
x->-3
X-+-3 x + 1 2x - 6 d) lim —-—-
x->+» 4 — X
b) lim
4 - X2
■ựx + 3 - 3
X + 2
lim -4^-
x-»+=° X + 1
c) lim -
x-*6 X - 6 ..	-2x2 + x - 1
f) lim	—	
X->+«,.	3 + X
Giải
Đáp số:
a) -4 d) -2
b) 4 e) 0 .
6
f) -X
Cho hàm số f(x) -	“ có đồ thị như trên hình.
X - 9
Bài 4 —
—
Tìm các giới hạn sau:
,.	3x - 5
a) lim—	—
’ xT2(X 2)2
2x - 7
b) lim
x->r X -1
2x-7
c) lim
X->1+ X 1
Đáp số: a) +x
Giải b) +x
c) -X
Bài 5
Quan sát đồ thị và nêu nhận xét về hàm số đã cho khi X -> -X, X -» 3“ và X -> -3+.
Kiếm tra các nhận xét trên bằng cách tính các giới hạn sau:
lim f(x) với f(x) được xét trên khoảng (-x; -3),
X->-=O	■
lim f(x) với f(x) được xét trên khoảng (-3; 3),	,
X—>3
lim f(x) với f(x) được xét trên khoảng (-3; 3).
Đáp sô
a) limf(x) = -00( lim f(x) =-00
x-+.'ì
b) limf(x) = o, limf(x) = -oo, x->3
Bài 6
lim f(x) = +00
x-»-3+
Tính:
a) lim(x4 - X" + X - 1)
X-++CO
b) lim(-2x': + 3x2 - 5)
X-4-CO
.	.. a/x2 + 1 + x
d) lim	
x5 _ 2x
c) lim -ựx2 - 2x + 5
V
ỳ’
x-a/2x-1
A
Tìm lim—Ị——	.
xX X - 12x + 11
Bài 1
Giải
0
Đáp số: a) +30
Giải
b) +30
c. Bài tập bổ sung
c) +--O
cl) -1
Ta có dạng vô định Nhân và chia tử và mẫu của phân thức với X + ->/2x - 1 , ta được
X - ự2x - 1 _ (x - \j2x - l)(x + ự2x -1)
x2-12x + ll (x2 -12x + ll)(x+ ỵ/2x-l) X2 - 2x + 1
(x - l)(x - ll)(x + -ự2x - 1)
X -1
(x - ll)(x + V2x-1) ’ với x * 1- x-1
X - V2x - 1
Do đó: Ịin?-fí	—	=
X->1 X2 - 12x + 11	X-+1 (x-ll)(x +V2x-1)
Tìm lim
Vxri - 3x
2x +1
(ỉiải
Bài 2
00
Ta có dạng vô đinh —. Với mọi x < 0, ta có
=|x|3 O'=XO
Do đó:
1-4
x’
/x6 - 3x
2x2 +1
2x2 +1
Vì lim .
1-4=1,
lim
XX V
X5
X—>-oo
<x X
VxH — 3x
nên lim
+00.
X—>-00
2x2 + 1
2 1
Bài 3
Giải
Ta có cỉạng vò định O.V.. Với mọi X > 2, ta có
(x-2)
■4
= (x-2)
_ -ựx - 2.Vx ạ/(x - 2)(x + 2) -ựx + 2
,,	Q\ I X	ạ/x - 2-Vx 0.5/2
Do đó: lim(x - 2)J—7—- = lim - -	; ■■■• = —2— = 0.
X -4	x-*2+ Vx + 2	2
Bài 4
Tìm lim(7l + X - 5/x).
X-»+ơ3
Giải
Ta cỏ dang vô định X - X. Nhân và chia biểu thức đã cho với biểu thức 5/1 + X + 5/x , ta được
/7——	/- _ (5/1 + X - Vx)(ạ/1 + X + 5/x)	1
VI + X - Vx = 	- r-	 = r	-	r= ■
Vl + x + Vx	Vl + x + Vx
Do đó: lim (Vl + X - Vx) = lim 	1	7= = 0.
	x->+«	x->+M VI + X + Vx	
(v/l + X + 5/x được gọi là biểu thức liên hợp của biểu thức 5/1 + X - 5/ĩ).
Dạng ị. a) Với X * 2, ta có
X3 - 8 _ (x - 2)(x" + 2x + 4) _ X2 + 2x + 4
X2 - 4 -	(x-2)(x + 2)	- x + 2
X3 - 8	,. X2 + 2x + 4
Do đó lim-
= lim -
= 3.
X2 - 4	X + 2
, ,	..	2x2 + 5x - 3	.. (x + 3)(2x-l)
b) lim — ——— = lim ——— 
x->(-3,+ (x + 3)	X-H-3I+ (x + 3)
2x-l
= lim 	— = -00
X^.(-.'1I+ X + 3
c) +x
. a/x3 + 1 - 1	.	X3
d) lim	—	= iim	:	—— 	
x^n X” + X	x->0 x(x + 1)(ựx?. F 1 + n
2
= lim	? ' •	= 0.
(x + l)(Vx3 +1 + 1)
- s
Tìm các giới hạn sau:
a) lim (x3 + 1L x-»(-n+	1
X
b) lim(x + 2).
x->+co
X —1
X2 -1
X3 + X
Bài 6
Giải
Dạng 0.x
a) Với X > -1 đủ gần —1(—1 < x < 0), ta có
(X3 +1)
X
= (x + l)(x2 - X + 1\
- ạ/x + l(x2 - X + 1).
X
(x — l)(x + 1) X
X —1
Do đó lim (x3 + 1). —7^-—= 0. x->(-D+	V X - 1
b) lim(x + 2)	= lim J(x + y,(* 7 - = L
x->+»	V X + X x->+“ Y X + X
Tìm các giới hạn sau:
a) lim
ạ/x2 + 1 - xì
b) linA;*2'1
x->+co \
/
x->1	X - X
Bài 7
Giải
°
Dạng X — oc và —.
lim (ạ/x2 + 1 - x) = lim .	. 	= 0
Vx2 + 1 + x
V2x - X2 - 1	2x - X2 - 1	_	- —(x - l)2
X2 - X	x(x - 1)(a/2x - X2 + 1) x(x - 1)(ạ/2x - X2 + 1)
1 - X
-	, ỉ'""~=ỹ	— với X + 1.	-	(1)
x(V2x - X +1)
. V2x - X -1 n Do đó lim	—	= 0.
K-+I X - X
D. Bài tập đề nghị
Bài 1
Tìm giới hạn của các hàm sô’ sau (nếu có):
a.)
lim -
x~>-2 2
- c)
lim °
X-»O
e)
lim
x->(-2)
Bài
2
a)
lim -
X—>+so
X + 3)3 - 27 X
x|x + 2|
v/x'’ + X - 11
X'1 + 8	. .	2x3 - 5x’- 2x - 3
	 	—	b) lim—;—.	-
+ llx +18	-	x^:’ 4x - 13x + 4x - 2
d)
x->0 2x
f) bm T 7 ““lự
z1 , L