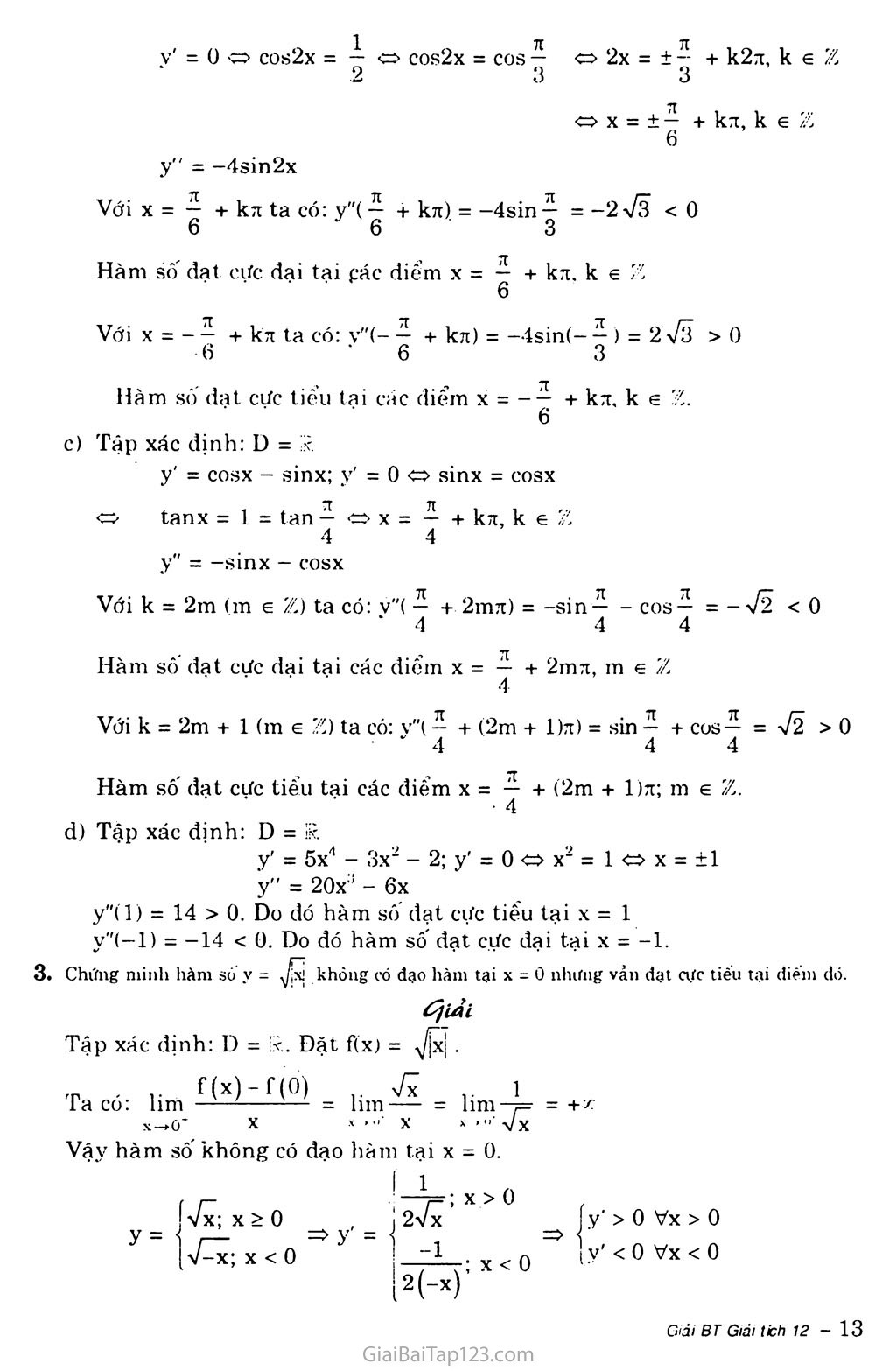Giải toán 12 Bài 2. Cực trị của hàm số

§2. cực TRỊ CỦA HÀM số
A. KIẾN THỨC CĂN BẢN
KHÁI NIỆM cực ĐẠI, cực TIỂU
Định nghĩa: Cho hàm sô' y = f(x) xác định và liên tục trên khoảng (a; b) (có thể a là -oo; b là +=o) và điểm Xo e (a; b).
Nếu tồn tại số	h > 0 sao cho	f(x) < f(x0) với	mọi X	e	(x0	-	h;	Xo +	h) và
X * x0 thì ta nói	hàm số f(x) đạt	cực đại tại x0.
Nếu tồn tại số	h > 0 sao cho	f(x) > f(x0) với	mọi X	e	(x0	-	h;	Xo +	h) và
X * Xo thì ta nói	hàm số f(x) đạt	cực tiểu tại x0.
ĐIỀU KIỆN ĐỦ ĐỂ HÀM so CÓ cực TRỊ
Định lí 1: Giả sử hàm số y = f(x) liên tục trên K = (x0 - h; x0 + h) và có đạo hàm trên K hoặc trên K\{x0), với h > 0.
Nếu f '(x0) > 0 trên khoảng (x0 - h; Xo) và f '(x) < 0 trên khoảng (x0; x0 + h) thì x0 là một điểm cực đại của hàm số f(x).
X
Xo - h
Xo
Xo + h
f'(x)
+
-
f(x)
	—	* f(CĐ)
X
Xo - h
Xo
Xo + h
f'(x)
-
+
f(x)
~	—• f(CT)	—
Nếu f '(X) 0 trên khoảng (x0; x0 + h) thì Xo là một điểm cực tiểu của hàm số f(x).
QUY TẮC TÌM cực TRỊ
Định lí 2. Giả sử hàm số y = f(x) có đạo hàm cấp hai trong khoảng
(x0 - h; x0 + h) với h > 0.
Khi đó: a) Nếu f '(x0) = 0; f "(x0) > 0 thì Xo là điểm cực tiểu; b) Nếu f "(Xo) = 0; f "(x0) < 0 thì Xo là điểm cực đại.
Các quy tắc tìm cực trị
Quy tấc I: 1. Tìm tập xác định.
Tính f(x). Tìm các điểm tại đó f'(x) bằng 0 hoặc f'(x) không xác định.
Lập bảng biến thiên.
Từ bảng biến thiên suy ra các điểm cực trị.
Quy tắc II: 1. Tìm tập xác định.
Tính f '(x). Giải phương trình f '(x) = 0 và kí hiệu X, (i = 1, 2...) là các nghiệm của nó.
Tính f "(x) và f "(Xj).
Dựa vào dấu của f "(x,) suy ra tính chất cực trị của điểm Xị.
B. PHƯƠNG PHÁP GIẢI BÀI TẬP
1. Áp dụng quy tắc I, hãy tìm các điểm cực trị của các hàm sô sau:
b) y = x4 + 2x2 - 3;
d) y = x3(l - X)2
e) y = ựx2 - X + 1
a) y = 2x3 + 3x2 - 36x - 10;
X = 2 (y = -54) x = -3 (ỹ = 71)
2 +00
a) Tập xác định: D = K
y' = 6x2 + 6x - 36; y' = 0 
Bảng biến thiên:
X
■ 71	+00
-co -—-	-54
Hàm sô' đạt cực đại tại X = -3 và yCĐ =71.
Hàm sô' đạt cực tiểu tại X = 2 và yCT = -54.
b) Tập xác định: D = K
y' = 4x3 + 4x = 4x(x2 + 1); y' = 0 X = 0 (y = -3) Bảng biến thiên:
-00 • 0 +00
■ +x
+x
Hàm sô' có điểm cực tiểu tại X = 0 và yCT = -3.
Tập xác định: D = R \ |0|
X2 -1
;y' = 0x2—l = 0
y' = i
X	X
Bảng biến thiên:
X = 1 (y = 2)
X = -1 (ý =-2)
—X
+x
+x
—X	"^-00
Hàm sô' đạt cực đại tại X = -1, yCB = -2 Hàm sô' đạt cực tiểu tại X = 1, yCT = 2.
Tập xác định: D = R •
y' = 3x2(1 - X)2 - 2x3(1 - x) = x2(l - x)(3 - 5x)
X = 1 (y = 0)
y' = 0 Ci-
3125
Bang biến thiên:
X
—00
0
3
5
1
+x
y'
+
0
+
0
—
0
+
y
00
108
+x
312ơ
0 —-
108
Hàm sô đạt cực đại tại X - - , ycw = ----- - 5	3125
_	 ; y' = 0 X = ị (y = ệ
2ựx2 - X +1	2	2
y' =
Hàm số đạt cực tiểu tại X = 1, y 0, Vx e K nên tập xác định: D - X 2x-l
Bảng biến thiên:
X
— X
1
2
+ x
y'
—
0
+
y
+x	
73
	» +0Õ
* 2
\]3
Hàm sô đạt cực tiểu tại X =	, yCT =
2
2. Áp dụng quy tắc II. hãy tìm các diêm cực trị cùa các hàm sô sau:
a) y = X4 - 2x2 +1:	b) y = sin2x - x; c) y = sinx + cosx; d) y = X5 - x:l - 2x + 1.
Ố^íảl
Tập xác định: D = X
y' = 4x:i - 4x = 4x(x2 - 1)
y' = 0 
X = 0 (y = 1)
X = ±1 (y = 0)
y" = 12x2 - 4
y"(0) = -4 0, hàm số đạt cực tiếu tại hai điểm X = ±1, ycT = 0.
Tập xác định: D = X y' = 2cos2x - 1;
y' = 0 cos2x = 77 cos2x - COS 77	o‘2x=±7 + k2x, k e z
2	3	3
 X = ± — + kx, k e z 6
y" = —4sin2x
Với X = 77 + k^ ta CÓ: y"(-77 + kĩi). = -4sin77 =5-2-73 <0
6	6	3
Hàm sô' đạt cực đại tại các điểm X - — + kn, k e X 6
71	71	-	7Ĩ	/77 /X
Với X = - — + kx ta có: ỵ”(- — + kn) = -4sin(— 77 ) = 2 V3 >0
6	‘	6	3
Hàm sô dạt cực tiếu tại các điểm X - - — + kĩt. k e z.
6
Tập xác định: D = R
y' = cosx - sinx; y' = 0 sinx = Cosx
 tanx = 1 = tan — X = — + kx, k e z 4	4
y" = -sinx - cosx
Với k = 2m (m 6 Z) ta có: ý"( — + 2mx) = -sin — - COS — - - yfỉ < 0
.	4	4	4
Hàm sô dạt cực dại tại các điếm X = — + 2mn, m e X • •	4
Với k = 2m + 1 (m e X) ta có: y"( — + (2m + l)x) = sin + COS-y = V2 > 0
•	4	4	4
Hàm só' đạt cực tiểu tại các điểm X = — + (2m + 1)71; m e X.
.4
Tập xác định: D = ÍK
y' = 5x4 - 3x2 - 2; y' = 0 0 X2 = 1 X = ±1 y" = 20x:ì - 6x
y"(l) = 14 > 0. Do đó hàm sô đạt cực tiểu tại X = 1 y''(-l) = -14 < 0. Do đó hàm sô' đạt cực đại tại X = -1.
3. Chứng minh hàm só y = 77 không có đạo hàm tại X = 0 nhưng ván đạt cực tiêu tại điẽm đỏ.
ốỊíảí
Tập xác định: D = K. Đặt f(x) = y]\x\ .
f(x)-f(0)	1
Ta có: lim 	-	 = lim—— = lim-^5 = + y
x-0'	X	X .«■ X X->" x/x
Vậy hàm sô' không có đạo hàm tại X = 0.
Ị 1 v ,,
■Tx; X > 0
7-x; X < 0
y’ > 0 Vx > 0 py' < 0 Vx < 0
Jàr>0 =1 y -1
-H-t: X < 0
í2(_x)
Bảng biến thiên:
X
—00
1
+00
Y'
-
1
+
y
0
4.
Vậy hàm số đạt cực tiểu tại X = 0.
Chứng minh rằng với mọi giá trị cúa tham sô’ m hàm số y = X3 - mx? - 2x + 1 luôn luôn có một điểm cực đại và một điểm cực tiểu.
Ta có y' = 3x2 - 2mx - 2
A' = m2 + 6 > 0 Vm e R nên phương trình / = 0 luôn có hai nghiệm phân
biệt và y' đổi dấu khi qua các nghiệm đó. Do đó hàm sô' luôn có một cực đại và một cực tiểu.
5.
Tìm a và b đế’ các cực trị cúa hàm sô’ y -
Ị a3x3 + 2axz - 9x + b đều lằ những sô dương và
5 1
Xu = - — là điềm cực đại. 9
(sỊiải
* Với a = 0 thì hàm số y = —9x + b không có cực trị
ycr = y(- -7-) = y( 1) =	+ 2a-9 + b= -—— + b > 0 b > ——
5a	3	5	5
ii) Với a > 0 ta có:
loại.
> nhận.
5	,x	 , .	,	9	5	81
xo =	- —	là	diêm cực đại	nên	- —	= - —	 a =	—
9	5a	9	25
và ycT = y( —) = -7- + — - — + b > 0 b > 777 a	3a a a	243
6. Xác định giá trị cùa tham sô’ m đế hàm só y = * + nlx + 1 đạt cực đại tại X = 2.
X + m
tfiai
Tập xác định: D = R \ Ị-mì
X-,,	1 X’ + 2mx + m2 - 1
Cách 1. y = 	— ■■■--„	
(x + m)
Nếu y đạt cực đại tại X = 2 thì y(2) = 0 » m2 + 4m + 3 = Oom = -l vm = -3 X = 0 X = 2
Vậy
a =
5
. . 36
b > 77
5
hoặc
81
25
400
243
i) Với m = -1 ta có: y' = 7—77: y' = 0 
(x - 1)-
Khi m = -1 hàm số không đạt cực đại tại X = 2.
ii) Với m = -3 ta có y' =
X -6x + 8 (x - 3)2
, y' = 0 
Vậy với m - -3 thì hàm sô' đạt cực đại tại X = 2. Cácli 2. Ta có thể sử dụng dấu hiệu II
m = -1
y đạt cực đại tại X = 2 => y'(2) = 0 «
2
m — -3
(x + mý*
m = -1 => y"(2) = 2 > 0 => Hàm sô' đạt cực tiểu tại X = 2 :
m = -3 => y"(2) = -2 Hàm sô' đạt cực đại tại X = 2 Vậy m = -3 thỏa yêu cầu bài toán.
c.
1.
2.
BÀI TẬP LÀM THÊM
Tìm cực trị của các hàm số sau: a) y = 2x3 + 3x2 - 36x - 10:
Tùy theo a hãy tìm cực trị của hàm số:
a) y = X3 - 2ax2 + a2x;	b) y = X + —.
X
b) y = x’ + 2x2 - 3;
3.
Cho hàm sô’ y =
X3 - mx2 + (m2 - m + l)x + 1. Xác định m để hàm sô’ 3
4.
đạt cực tiểu tại X = 1.
Định m để hàm sô’ y = 2x3 - 3(2m + l)x2 + 6m(m + l)x + 1 đạt cực dại, cực tiêu tại XI, X2. Chứng minh rằng khi đó X2 - XI không phụ thuộc vàó m. Đớp số: XI = m: X2 = m + 1.
5.
Chứng minh rằng hàm sô’ y -
X" + 2x + rn
X' + 2
luôn luón có một cực đại và
một cực tiểu.