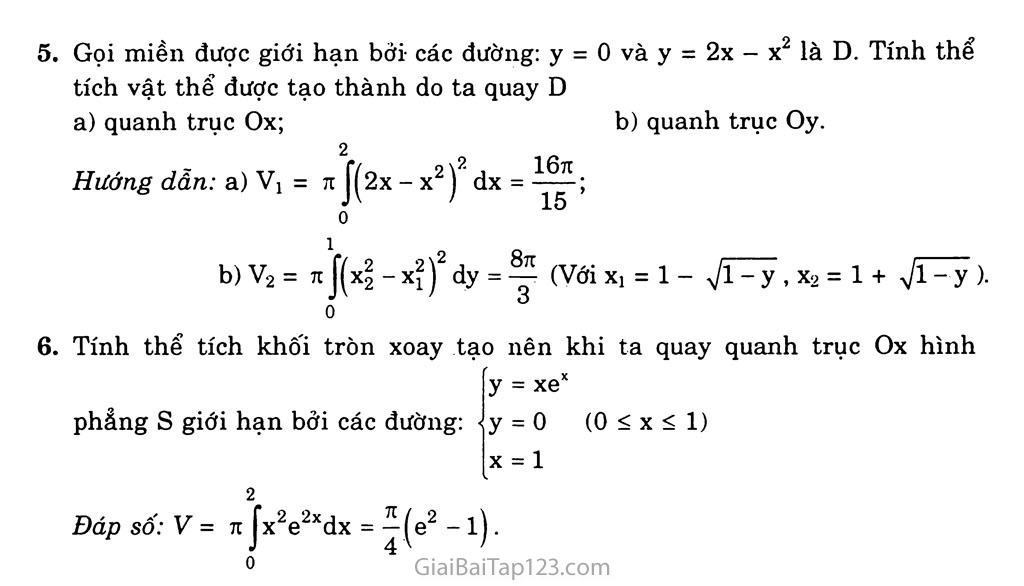Giải toán 12 Bài 3. Ứng dụng của tích phân trong hình học

§3. ỨNG DỤNG CỦA TÍCH PHÂN TRONG HÌNH HỌC
A. KIẾN THỨC CÀN BẢN
Diện tích hình thang cong
Cho f(x) liên tục trên [a; b]; diện tích hình phẳng giới hạn bởi các đường:
b
y - f(x), y = 0, x = a, x = b tính theo công thức: s = J|f (x)ịdx a
Diện tích hình phẳng
Hình phẳng giới hạn bởi 2 đường cong (Ci) và (Cỉ/ có phương trình y = f 1 (x), y = h(x) và các đường thẳng X = a; X = b (với fi(x) < Í2(x) Vx e [a; b]
b
có diện tích: s - Jịf2 (x) — í, (x)ịdx
a
Thê tích hình xoay tròn
Thể tích hình xoay tròn do hình phẳng giới hạn bởi các đường y = f(x); trục Ox, các đường thẳng X = a: X = b quay quanh Ox là:
b
ỉ) V = 7tJ[f(x)]2 dx; a
ii) f(x) > g(x) > 0 Vx e [a; b] hoặc 0 > f(x) > g(x) Vx e [a; b] b
thi V = 7iJỊf2(x)-g2(x)Ịdx .
B. PHƯƠNG PHÁP GIẢI BÀI TẬP
Diện tích hình phẳng giới hạn bởi y = f^x), y = f2(x), X = a, X = b là:
b
s = J|f1(x)-f2(x)|dx (1) ã
Để bỏ giá trị tuyệt đối trong (1) ta thực hiện một trong hai cách:
Cách 7; Xét dấu fi (x) - f2(x) trên [a; b]
Giải phương trình: h(x) - f2(x) = 0 trên đoạn [a; b]. Giả sử phương trình có hai nghiệm c, d (c < d). Khi đó, f,(x) - f2(x) không đổi dấu trên các đoạn [a; c], [c; d], [d; b]. Trên mỗi đoạn đó, chẳng hạn trên đoạn [a; c], ta có
c	c
J|f1(x)-f2(x)|dx = J[f1(x)-f2(x)]dx a	a
Cách 2:\/ẽ đồ thị (Cì): y = f,(x) và (C2): y = f2(x).
c) y = (x - 6)'2, y = 6x - X2.
Tính diện tích hình phăng giới hạn bởi các đường: a) y = X2, y = X + 2;	b) y = |ln x|, y = 1;
éỳisỉi
à) Phương trình hoành độ giao điểm của hai đường cong là:
X2 = X + 2 X2 - X - 2 = 0 o
Diện tích hình phẳng đã cho là
s = fix2 - X - 2j dx = f(x2 - X - 2)dx = f	- 2x
-1	I-1	l 3 2	.
b) Phương trình hoành độ giao điểm của hai đường cong là rx = e
.,	,	„ mx = 1
I lnx I = !.	
-1
(đvdt)
lnx = -1
s = J]l - |lnxjdx
l/e
1	e
= J(1 + lnx)dx +	- lnx)dx
l/e	1
Tính Jln xdx iu = lnx
Đặt
dv = dx
=>
du =
dx
Suy ra Jinxdx = XInX - Jdx = xlnx-x + c Vậy một nguyên hàm của y = lnx là F(x) = xlnx - X.
Do đó s = xlnx)J/e + (2x - xlnx)|j = -+2e-e-2= — + e- 2 (đvdt).
c) Phương trình hoành độ giao điểm của hai đường cong là:
V Í3
(x - 6)2 = 6x - X2 	“
X = 6
6	6
Vậy s = JỊ(x - 6)2 - (6x - X2 jjdx = J2^x2 - 9x + 18)dx 3	3
V Í3
= 9 (đvdt).
(x - 6)2 = 6x - X2 X2 - 9x + 18 = 0 
Tính diện tích hình phăng giới hạn bởi đường cong y = X2 + 1, tiếp tuyến với đường này tại điểm M(2; 5) và trục Oy.
Ta có M(2; 5) e (C)
y' = 2x => y’(2) = 4
x2	 	 r- ■	
Parabol y = 2 chia hình tròn có tâm tại gô'c tọa độ. bán kính 2v2 thành hai phần. Tìm tỉ sô’ diện tích của chúng.
zỹzđ’z
Phương trình đường tròn tâm 0 bán kính 272 là:
(C): X2 + y2 = 8. Tung độ giao điểm của (C) và (P) là:
y2 + 2y - 8 = 0 
y = -4 (loại) y = 2
y - 2 X = ±2
Gọi S] là diện tích giới hạn bởi (C) và (P) ở phía trên trục hoành.
2 	 ■ 2 2 	 3
Ta có s, = 2 1(78-X2 -^-)dx = 2 |78-x2dx--y-
0 2 0 3
X
0
2
t
0
71
4
Đặt X = 2 72 sint => dx = 2 72 costdt Đổi cận:
it	K
2 _____	4 	 4
Suy ra: J 78 - x2dx = JV8cos2t .2\/2 costdt = 8 Jcos2 tdt 0 0	0
71
6k + 4
= 4 J(1 + cos2t)dt = 4^t + Ỉsin2t j = 4^ + ^j = K + 2
Vậy Si = 2k + 4 - Ệ = 2k + 4 3	3
s2 = 8k - Si = 6k -
18k - 4
-rjs s2 18k-4 9k-2 Vậy ~ - -7——r = - —r
Sj 6k + 4 3k + 2
c) y = tanx, y = 0, X = 0, X =	.
Tính thê tích khối tròn xoay do hình phàng giới hạn bới các đường sau quay quanh trục Ox: a) y = 1 - X2, y = 0 b) y = cosx. y = 0, x = 0, X = JI
Ốịiảl
Giao điểm của hai đường y=l-x2vày = 0 1àl-x2 = 0x = ±l c) Thể tích cần tìm là
1	V,
Vậy v= K J(l-X2) dx = K J(l - 2x2 + X4 jdx = K
-1	-1
16
X-77X3 +—	= -77- (đvdt).
b) Thể tích cần tìm là:
K	K	n (	1	\
V = K Jcos2xdx =	J(1 + cos2x)dx = X + — sin2x I
0	0	2^27
'1-1
K2
2
15k
7t	7t
v= K Jtan2 xdx = K —^2	l^dx =K(tanx-x)Ẹ = K^l - (đvdt).
Cho tam giác vuông OPM có cạnh OP năm trên trục Ox. Đặt POM = CI, OM = R 00. Gọi V là khối tròn xoay thu được khi quay tam giác đó xung quanh trục Ox.
y ■
Tính thế’ tích cùa V theo a và R
M
Tìm a sao cho thế' tích của V lớn nhất.
éjìải
a) Ta có OP = OM.cosa = R.cosa PM = OM.sina = Rsina
=> MíRcosa; Rsina)
Phương trình đường thẳng OM: y = (tana).x
Thể tích của V là:
Rcosa	3
V = 7t I x2tan2adx = 7itan2a.
J	3
0	đ
b) Đặt t = coscc => t e
71 R:ì
vì a e
0;
V' = —^-(1 - 3t2); V' = 0 . 3
Rcosa 7lR3
= -7— (cosa - cos3a) 0 3
—■p3
, ta có V = —— (t - t3); 3
73
t = - -y= (loại)
73
Vậy maxV(a) = maxV(t) = VCĐft = -HÌ = 2^R •
H	I TsJ 27
(trong đó cosa = ~H hay a = arccos H ).
73	73
c. BÀI TẬP LÀM THÊM
1. Tính diện tích của hình phăng giới hạn bởi các đường sau:
a) X = 0, X = 1, y = 0, y = 5x4 + 3x2 + 3; b) y = X2 + 1, X + y = 3; c) y = X2 + 2, y = 3x;
e) y - Inx, y = 0, X = e;
Đáp số: a) 5
d) y = 4x - X2, y = 0; g) X = y3, y = 1, X = 8.
»!
c,ì
d)
32
e) 1
g)
17
Tính diện tích giới hạn bởi các đường X + y = 0; X2 - 2x + y = 0.
Hướng dẫn: s = J[(-x + 2x) - (-x)]dx = Ệ. 0
Cho D là miền được giới hạn bởi các đường: y = 0; y = 7cos4x + sin’x ;
X = H X - 71. Tính thể tích khối tròn xoay tạo nên do ta quay miền D 2
quanh trục Ox.
Hướng dẫn: V = 71 J^cos4 X + sin4 xjdx = 7t + CJS 4* dx =	.
Ă	31
2	2
Tính thể tích của khôi tròn xoay^tạo nên do ta quay hình (H) quanh trục Ox với (H) là hình được giới hạn bởi các đường:
y = 0; y = 7cosGx + sincx ; X = 0; X = |-
Đáp số: V =
5ti2 16 ■
5.
Gọi miền được giới hạn bởi- các đường: y = 0 và y = 2x - X2 là D. Tính thể tích vật thế’ được tạo thành do ta quay D
a) quanh trục Ox;	b) quanh trục Oy.
2 2 16 Hướng dẫn: a) Vj = 71 J(2x - X2) dx = —
0
6.
1
b) v2 = 7t J(x2 - X2) dy = -y (Với X] = 1 - ựl-y , x2 = 1 + ựl-y 0
ĩ ~ T- 1-1* ít z X —- 	X	Ẵ — 1 — 1— - X 7-7	V r	« 7-h W-7 1-7 ị-vtl » Zì I 1*17 h 7 l~\
Tính thể tích khôi tròn xoay tạo nên khi ta quay quanh trục Ox hình
y = xex
■ y = 0	(0 < X < 1)
X = 1
phẳng s giới hạn bởi các đường:
2
Đáp số: V = n Jx2e2xdx = 4 (e2 - l). 0