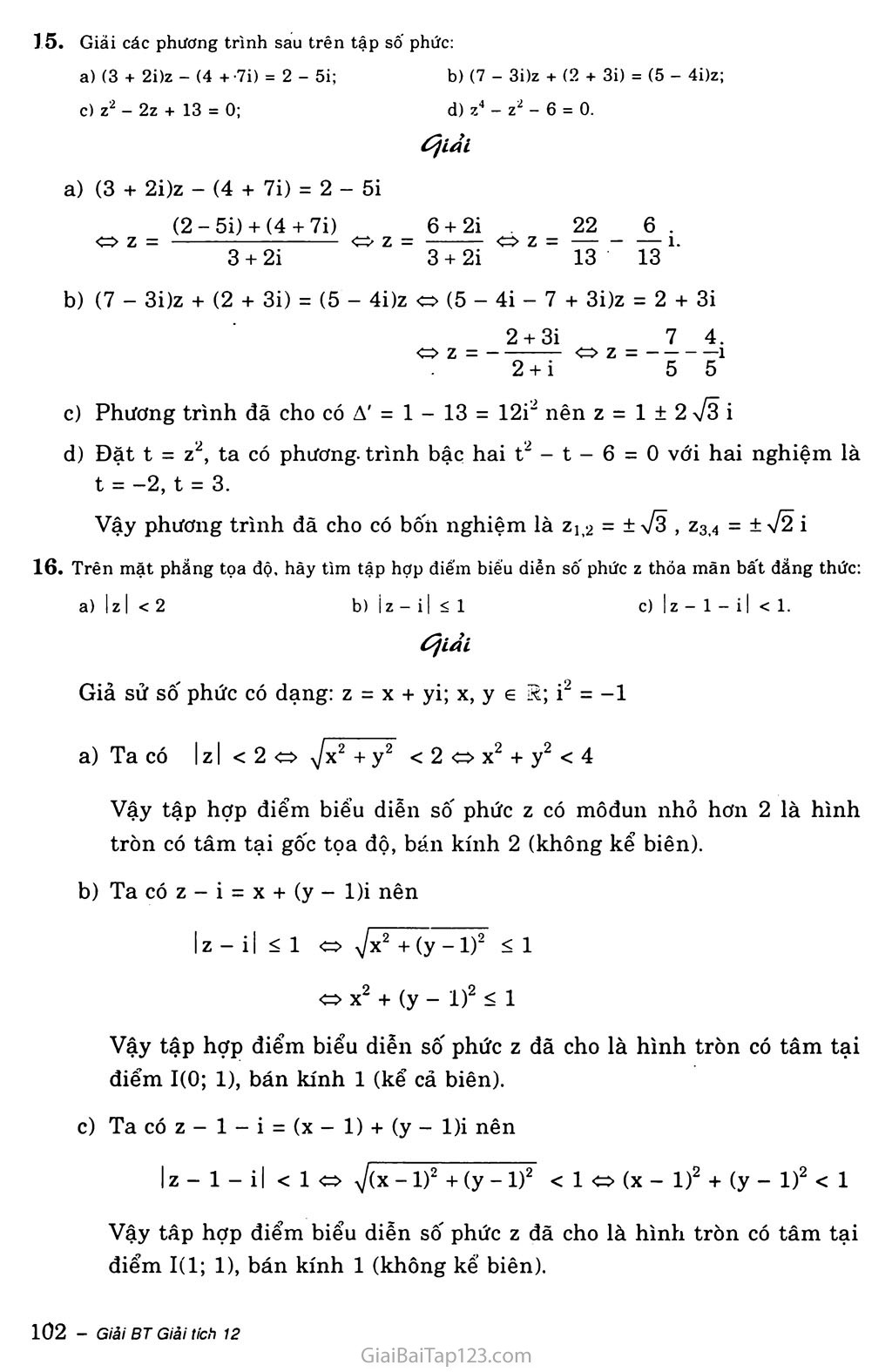Giải toán 12 Ôn tập cuối năm
ÔN TẬP CUỐI NĂM
1. Cho hàm số fix) = ax2 - 2(a + l)x + a + 2 (a * 0).
Chứng tỏ rằng phương trình Rx) = 0 luôn có nghiệm thực. Tính các nghiệm đó.
Tính tổng s và tích p của các nghiệm của phương trình Kx) = 0. Khảo sát sự biến thiên và vẽ đồ thị của s và p theo a.
tfiải
Vì a + (-2a - 2) + a + 2 = 0 nên phương trình fix) = 0 luôn có hai
nghiệm thực Xi = 1; x2 = a + 2 a
a a
2
Khảo sát sự biến thiên và vẽ đồ thị của s = 2 + —;
a
Tập xác định: R \ (01
2
S' = - —5- < 0, Vạ # 0 nên hàm số nghịch biến trên từng khoảng (-00; 0) a
và (0; +00)
a
—00
0
+CO
S'
— —
s
2 -----
+c0'
* —00 ~~~
— 2
Tiệm cận đứng a = 0; tiệm cận ngang s =
Giao của (Cj): s = 2 + — với Oa: s = 0 => a
2
Đồ thị (Cl): s = 2 + — là đường nét liền a
Tịnh tiến đồ thị (Ci) song song với trục tung xuôìig dưới 1 đơn vị ta được đồ thị
2. Cho hàm sô' y = - i X3 + (a - l)x2 + (a + 3)x - 4 3
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm sô' khi a = 0.
Tính diện tích hình phẳng giới hạn bởi (C) và các đường thẳng y = 0, X = -1, X = 1.
(C2): p = 1 + — (nét đứt), a
Diện tích hình phẳng cần tìm là:
s = J”~x3 - X2 + 3x - 4 dx = j[ỉx3 + X2 - 3x + 4^j dx
1 4 1 3 oxz .
-77-X + ~x ‘ - 3™- + 4x 12 3 2
= (đvdt) 3
3. Cho hàm sô’ y = X3 + ax2 + bx + 1
Tìm a và b đề đồ thị của hàm sô’ đi qua hai điểm A(l; 2) và B(-2; -1).
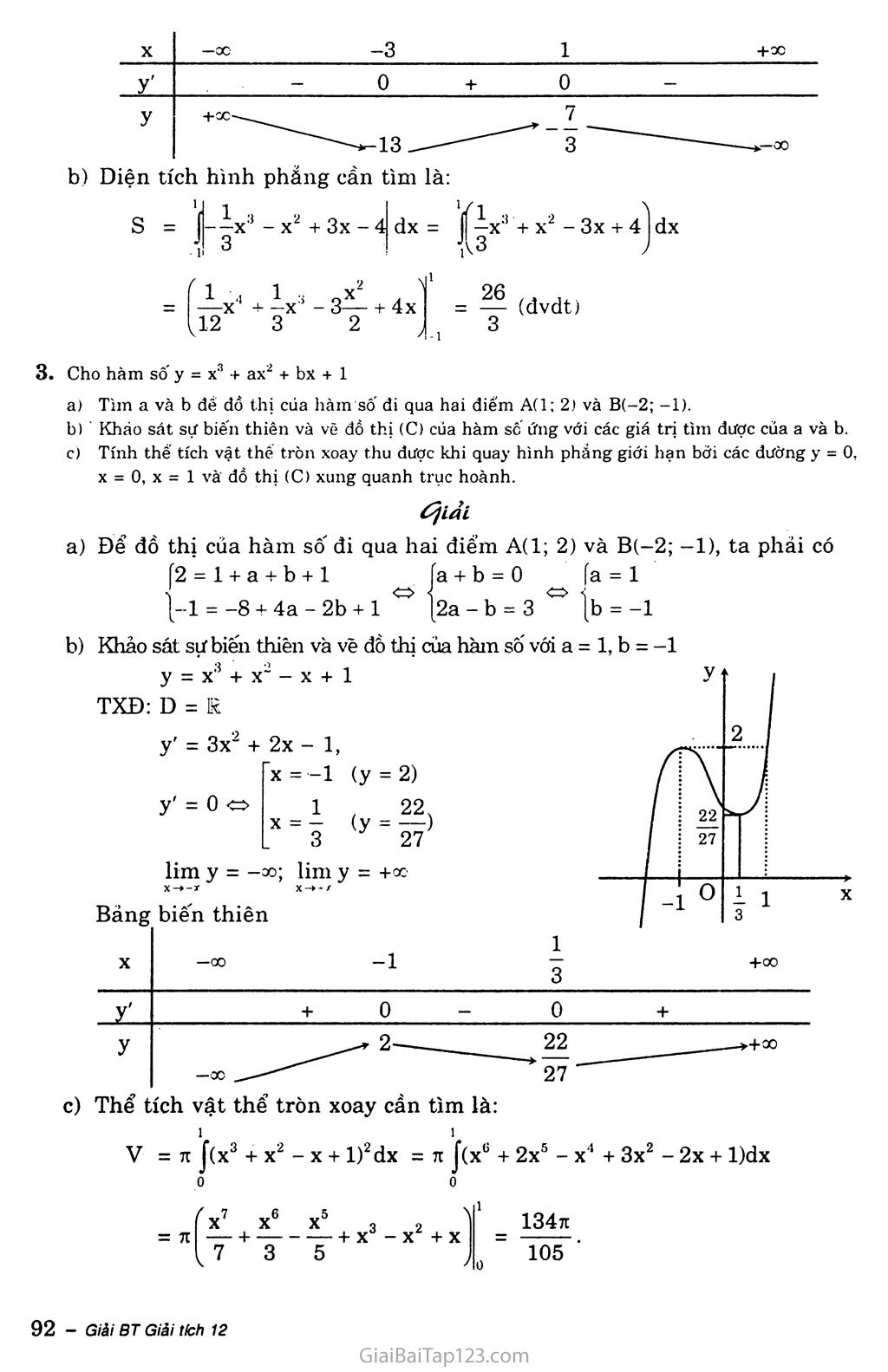
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm sô’ ứng với các giá trị tìm được của a và b.
Tính thế’ tích vật thể tròn xoay thu được khi quay hình phắng giới hạn bởi các đường y = 0, X = 0, x = 1 và đồ thị (C) xung quanh trục hoành.
Ốịiải
Để đồ thị của hàm sô' đi qua hai điểm A(l; 2) và B(-2; -1), ta phải có [2 = l + a + b + l ia + b = o |a = 1
ị-1 = -8 + 4a - 2b + 1 ° [2a - b = 3 “° |b = -1
A ■> ■> - 1 4 •} t*
Xét. chuyến động thẳng xầc định bới phương trình: s(t) = Ị t4 - t3 + - 3t,
trong đó t được tính bằng giây và s được tính bằng mét.
. Tính v(2), a(2), biết v(t), a(t) lần lượt là vận tốc, gia tốc của chuyền động đã cho.
Tim thời điểm t mà tại đó vận tốc bằng 0.
ốjiải
Ta có vận tô'c: v(t) = s'(t) = t3 - 3t2 + t - 3, với t = 2 thì v(2) = -5 (m/s)
Gia tô’c: a(t) = v'(t) = 3t2 - 6t + 1, với t = 2 thì a(2) = 1 (m/s2)
v(t) = 0 t3 - 3t2 + t - 3 = 0 «• (t2 + l)(t -3) = 0«t = 3 (s).
Cho hàm số y = X4 + ax2 + b
a) Tính a, b đế hàm số có cực trị bằng khi X = 1.
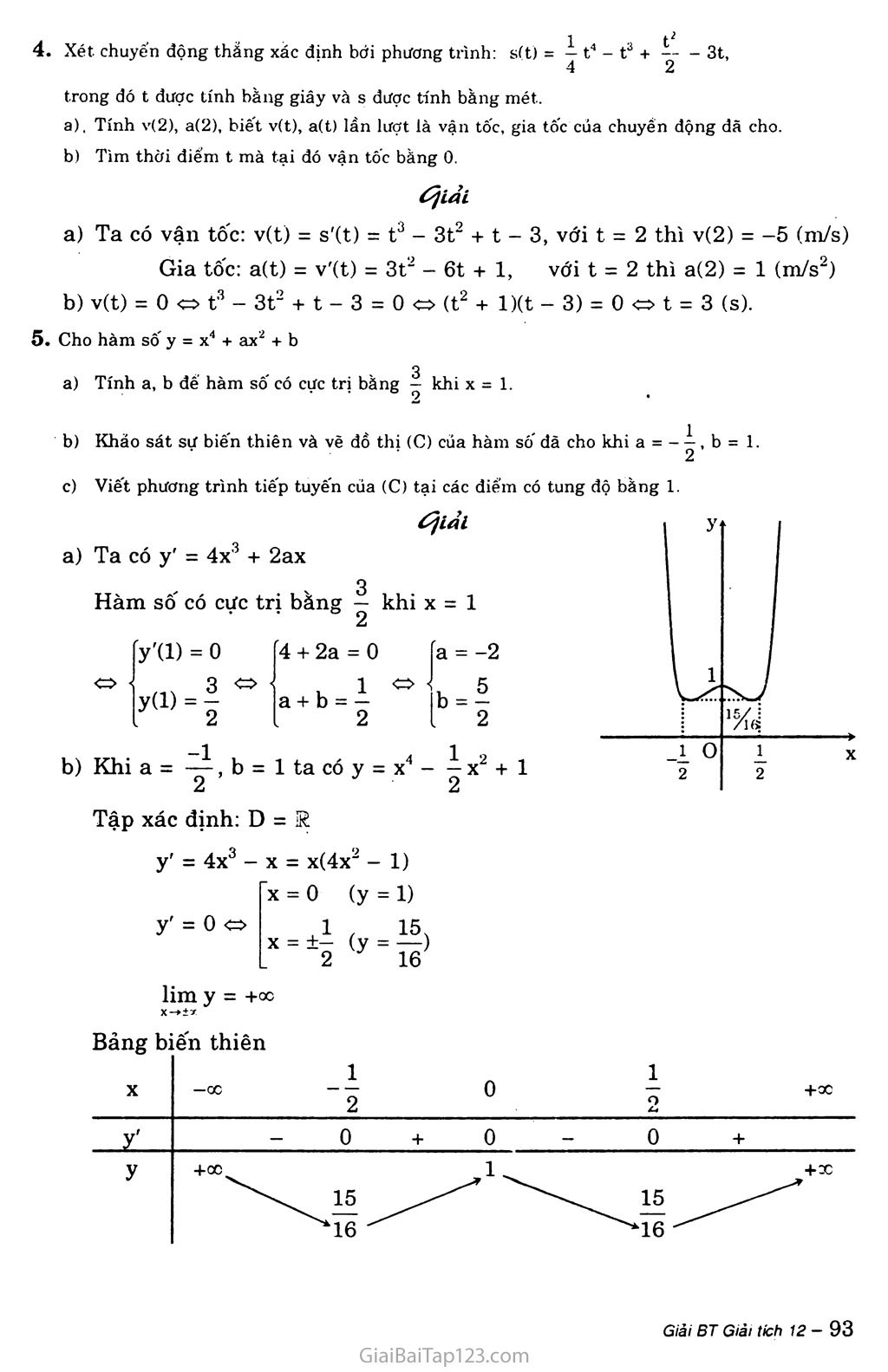
Khảo sát sự biến thiên và vẽ đồ thị (C) cúa hàm số đã cho khi a = -ì, b = 1.
Viết phương trình tiếp tuyến của (C) tại các điểm có tung độ bằng 1.
Ốịiải
a) Ta có y' = 4x3 + 2ax
Hàm sô' có cực trị bằng khi X = 1 2
y'(l) = 0
4 + 2a = 0
3
ly<1)=f I
1 « a + b = —
2
5
a =-2
b) Khi a = —, b = 1 ta có y = X* - 4 X2 + 1 2 2
Tập xác định: D = K
y' = 4x3 - X = x(4x2 - 1)
X = 0 (y = 1)
y' = 0
„ 1 ,15,
X = +£■ (y = 3^) 2 16
lim y = +OC
Ta có y = 1 X4 - 4 X2 + 1 = 1 X4 - ị X2 = 0 2 2
o x2(x2 - ị ) = 0 e>
X = ±-
72
Ta có ba tiếp điểm A(0; 1), B(-^=; 1), C(—7=; 1)
X + m - 1
Kháo sát sự biến thiên và vẽ đồ thị (C) của hàm số khi m = 2.
Viết phương trình tiếp tuyến d của đồ thị (C) tại điếm M có hoành độ a * -1.
Tính khoảng cách từ điếm K-l; 1) đến tiếp tuyến d. Xác định a để khoảng cách đó là lớn nhâ’t.
Ốjiải
a) Khi m = 2 ta có y =
x-2 x + 1
TXĐ: D = R \ {-1} 3
y =
> 0, Vx * -1
(x +1)2
Tiệm cận đứng: X = -1; tiệm cận ngang: y = 1
X
—oc —1 +00
y'
+
+
y
*+CC
1
Giao điểm với trục Ox tại (2; 0); Giao điểm với trục Oy tại (0; -2).
b) Với X = a => y =
(a *-1)
và f(a)=
3
(a +1)2
Phương trình tiếp tuyến d có dạng
3 a-2
y = 7' /-n2 (x - a) + 7—7 (a +1) a +1
(a + l)2y = 3(x-a) + (a - 2)(a + 1) 3x - (a + l)2y + á2 - 4a - 2 = 0
Khoảng cách từ K-l; 1) đến d là
H = -- + \ + = Tẽ (áp dụng: A + B > 2a/ÃB)
79 + (a + l)4 76(a + l)2
=> maxh = Tẽ khi và chỉ khi (a + l)4 = 9
a = —1 ± 73 .
2
7. Cho hàm sô’ y = —í— .
2-x
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm sô’ đã cho.
Tìm các giao điểm cùa (C) và đồ thị cúa hàm số y = X2 + 1. Viết phương trình tiếp tuyến của (C) tại mỗi giao điểm.
Tinh thể tích vật thế’ tròn xoay thu được khi quay hình phăng H giới hạn bởi đồ thị (C) và các đường thẳng y = 0, x = 0, X = 1 xung quanh trục Ox.
a) Tập xác định: D = K \ )2|
y = (2 - X)2 > °’ Vx * 2
X
-co
2
+CO
y'
+
+
y
'S' +CO
—cc
Tiệm cận đứng X = 2, tiệm cận ngang y - 0 Bảng biến thiên
Hoành độ giao điểm của (C) với của phương trình:
đồ thị hàm số y = X2 + 1 là nghiệm
— - = X2 + 1 2 = (x2 + 1)(2 - x) với X * 2
2 - X
x(-x2 + 2x - 1) = 0
Ta có f' (x) =
2
(2 - x)2
x=o=>y=lvà f’(0) =
phương trình tiếp tuyến có dạng y = -- X + 1;
• X = 1 => y = 2 và f' (1) = 2
=> phương trình tiếp tuyến có dạng y = 2(x - 1) + 2 hay y = 2x
Thể tích vật thể tròn xoay cần tìm là:
= đx = 4xf-
dx 1
= 4ít-
,(2-x)2 2-x
8. Tìm giá trị lớn nhát, giá trị nhó nhát cũa các hàm sô”:
fix) = 2x3 - 3xy - 12x + 1 trên đọạn [-2; -ị
L 2J
fix) = x21rx trên đoạn [1; e]
4il| 1 - I = 2x (đvdt).
fix) = xe ' trẽn nứa khoảng [0; +x)
fix) - 2sinx + sin2x trên đoạn .
D = [-2; I ]. HSLT trên
-2;
f (x) = 6x2 - 6x - 12; f (x) = 0 o
X = -1 6 D X = 2.e D
5 33
Ta có f(-l) = 8, f(2) = -19, f<-2) = -3, f(|) = -
Vậy mạxf(x) = 8, minf(x) --19.
D = [1; e]. HSLT trên [1; e]
f(x) = 2xlnx + X = x(21nx + 1) > 0 Vx e [1; e] Do đó: mạxf(x) = f(e) = e2, minf(x) = f(l) = 0
x?ì) xliĩ
D = [0; +oo)
f '(x) = e“x - xe~x = e’*( 1 - x)
f'(x) = 0 x = 1 ; lim f(x) = 0, f(0) = 0, f(l) = —
x-»+co e
X
0 1 +»
v'
+ 0 -
y
■
ẽ 0
Bảng biến thiên:
mạxf(x) = f(l) = —; minffx) = fio) = 0
xel) p xi)
f (x) = 2cosx + 2cos2x = 2(cosx + 2cos2x - 1);
cosx = -1
f(x) - 0 2cos2x + cosx - 1 = 0 1
cosx = -7
L 2
Ta có f(0) = fU) = 0, fM = 3^3 , ffặ-ì = -?
<3 J 2 I 2)
WA.. X-Z..X JnÌ = mir.f(x) =fi~i =-2.
2 " 0 ; 2 J
Vậy maxf(x) = f
xeD
9. Giải các phương trình sau: a) 132* * - 13x - 12 = 0; c) logự5 (x - 2)log5x = 2.1og.i(x - 2);
X ~ 71
7t
X = 77
3
b) (3X + 2SX3* + 3.2s) = 8.6X d) log2 X - õlogxx + 6 = 0.
ốỊiảl
Đặt t = 13x (t > 0) ta có phương trình 13t2 - t - 12 = 0
t = 1 13x = 1 X = 0. Vậy s = (0!.
Chia hai vế phương trình cho 6X ta được
3X+2X 3X+3.2X
2X
1 + 31?
Đặt t = I 2 I (t > 0) ta có phương trình
(t + 1)(1 + |) = 8ot2-4t + 3 = 0o
ế) =3
t = 1
t = -777 (ioại)
13
X = 0
X = Iog;ì3 • Vậy s <°; loểs3ì
2 2
log„(x-2) = 0 log6x -1
c) Điều kiện: X > 2. Ta có:
log 5 (x - 2).log5X = 21oga(x - 2) 21og:i(x - 2).logox = 21og;ì(x - 2)
o lơg3(x - 2).(log5X - 1) = 0 c?
Vậy s = (3; 51.
d) Điếu kiện: X > 0
Đặt t = log2x ta có phương trình ít = 2
t - 5t + 6 = 0
t = 3
ìog2x = 2 ]og2x = 3
2*
. Vậy s = (4; 81.
Iog2(x2-n
10. Giải các bất phương trình sau: a) < 2
3 — 2
c) log2x + 31ogx > 4
Ốịlải
a) Bâ't phương trình đã cho tương đương với 2
b)
d)
1 - log4 X < 1 1 + log2 X 4
Đặt = I 2 J (t > 0), ta có bất phương trình
1 3/2 +00
+ 11-0 +
3 2
2t - 3
t-1
0 ^ Hr <1 hoặc o
Vậy nghiệm của bất phương trình đã cho là X 1 s = (-co; 0) o [1; +oc)
b) Bất phương trình đã cho tương đương với hệ
X2 - 1 > 0 log2(x2 - 1) < 0
X2 - 1 > 0
1 < X2 < 2
(X2 - 1 < 1
1 -72 < X < —1 hoặc 1 < X < 72 Vậy tập nghiệm của bất phương trình đã cho là:
s = (-72 ; -1)0(1; 72 ) c) Điều kiện X > 0, đặt t = logx ta có
t2 + 3t - 4 > 0 t lo 10 Vậy tập nghiệm của bất phương trình đã cho là:
8 = 0;
io; —Ị I 10000J
o [10; +oo)
Điều kiện X > 0, đặt t = log2x, ta có bất phương trình l_|t
——-— Ị 3 1
1 + t 4 4(1 +1)
0 2 -11 +X 2 '
\ỉtfỉtỉĩ\ ■*
-|| + 0
Vậy tập nghiệm của bất phương trình đã cho là s = ° [2; +oo).
11. Tính các tích phân sau bằng phương pháp tích phân từng phần:
a)
ln xdx ;
b)
f xdx J sin2 X
c)
J(n-x)
sin xdx ;
d)
0
J(2x + 3) -1
úịlàl
, dx
r.. 1_„ du = —
u = Inx X
Đặt ( => ,
dv = Vxdx 2 J
3
e4 9 3 ọe4 1 9 e4 4 _|e4 4
IVxlnxdx = ^x2lnx - 4 fx2dx = 47x^lnx - 37VX3 = ^-(5e6+ 1)
J 3 Ij 3 J 3 1 9 , 9
TX-X [u = x ídu = dx
Đặt ( 1 => 1
dv = . dx IV = -cotx
sin X
x/f xdx
n/2 n/2
fCOSX ,
n/2
F= -xcotx
+ I dx = -xcotx
+ ln|sinx|
J6sin X
;Ksinx
71/6 */6
71/6
x/2
7t / 6
7173
+ ln2
c) Đặt
u = 71 - X dv = sinxdx
du = -dx V = -cosx
71 71 7t
J71 - x)sinxdx = -(71 - x)cosx - Jcosxdx = -(71 - x)cosx
- sinx
= 7Ĩ
d) Đặt
u = 2x + 3 dv = e"xdx
du = 2dx V = -e‘x
0 ° °,
J(2x + 3)e'xdx = -(2x + 3)e"x +2 Je"xdx = -(2x + 3)e"x -1 -1 -1
-2e'
= 3e - 5.
12. Tính các tích phân sau bằng phương pháp đổi biến số:
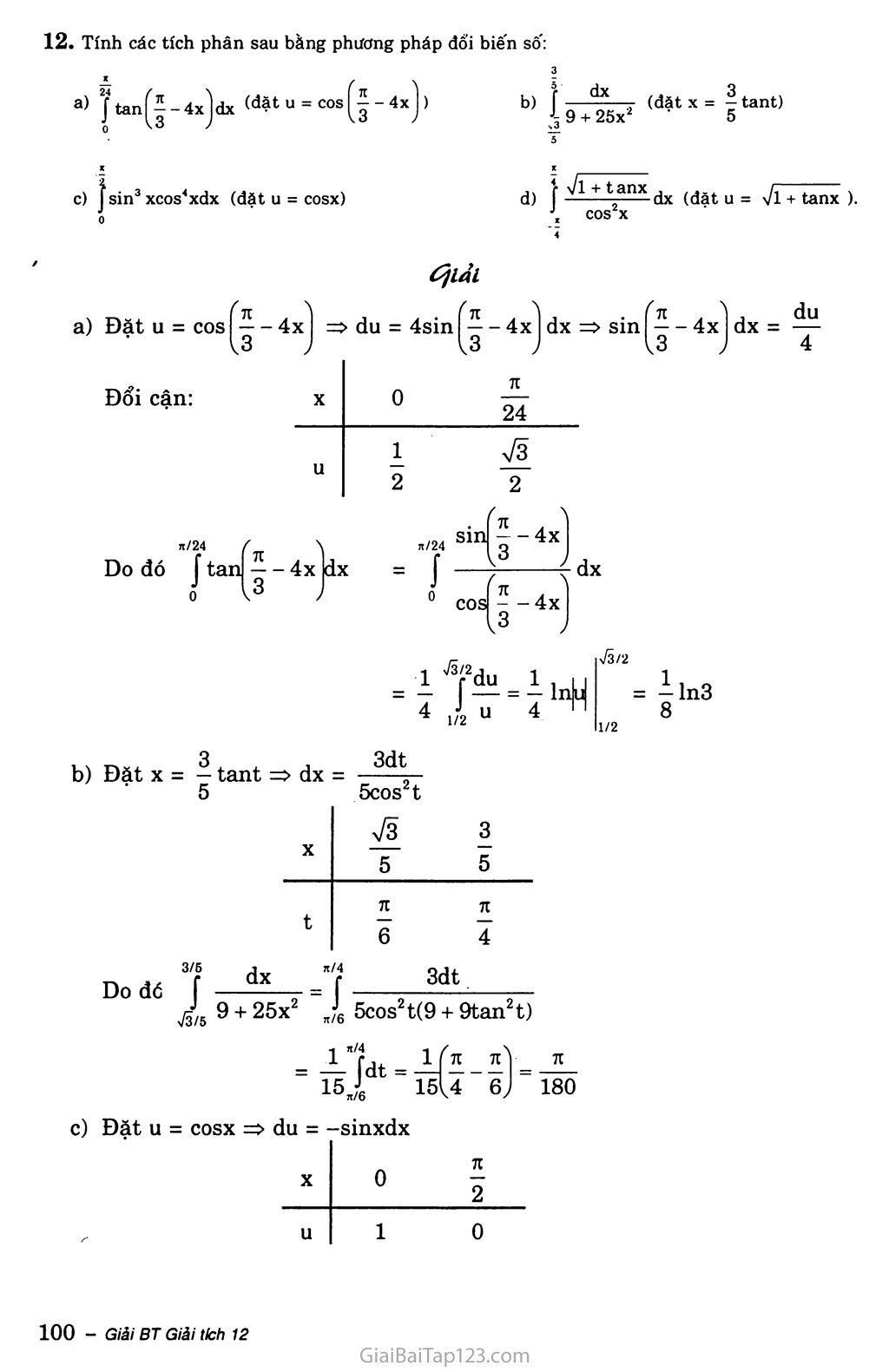
a> Jtan(j-4x)dx (đặt u = COS - 4x}) c) J sin3 xcos’xdx (đạt u = cosx)
f -—d* (đặt X = Ệ tant)
■L 9 + 25x2 5
X
d) f — + t an* dx (đặt u = ựl + tanx ). \ COS X
Ốịiải
du
Đổi cận:
X
0
7Ĩ
24
1
73
u
2
2
a) Đặt u = COS -4x => du = 4sinP-4x dx => sin 7-4x dx = <3 ) 13 J 13 J
sinl - 4x
Do đó
rc/24 / \ 7t/24
6 ịtan^-4xjdx = I
° cosfI - 4x
dx
- 1 'Vèỉ - ì UJ
4 ,J u 4lnH
1/2 u
Vã/2
1/2
= 7ln3
8
b) Đặt X = tant => dx =
5
3dt
5cos2t
73
5
3/5 J n/4
Do đó =
71
6
71
4
3dt
ự//6 9 + 25x 5cos t(9 + 9tan t)
= ^fdt=M-ỉ)=-ỉ- 15J 15\4 6j 180
c) Đặt u = cosx => du = -sinxdx
X
0
71
2
u
1
0
n/2 -0
Do đó Jsin3xcos4xdx = J (u2 - l)u4du
0 1
0
= J (u6 - u4)du =
1
/ 7
,6>
u
u
y
35
d) Đặt u = Vl + tanx hay u2 = 1 + tanx => 2udu =
dx
COS2X
X
71
~4
71
4
u
0
7?
A
n , n/r Vl + tanx J '' r 2, _ 2 .3 Do đó —dx = 2u du = ~u
J/4 cos x 0 3
13. Tính diện tích hình phăng giới hạn bởi các đường: a) y = X2 + 1, X = -1, X = 2 và trục hoành
4V2
3
b) y = lnx, X = -, X = e vậ trục hoành, e
_ , 2 fx3 Ý
Diện tích hình phẳng cần tìm là: s = J(x2 + l)dx = + XJ =6
e e e
Diện tích cần tìm là: s = JJlnxjdx = - J lnxdx + J lnxdx
1 1 1
e e
dx
Đặt u = lnx, dv = dx => du = — , V = X.
X
Ta có: ýnxdx = xlnx - J dx = x(lnx - 1) + c
„ „ ’ „ _.e 7 1
Do đó s = -x(lnx - 1) + x(lnx -1) = 2 1- -
1/e 1 V e
14. Tìm thể tích vật thế' tròn xoay thu được khi quay hình phẳng giới hạn bởi các đường y = 2x2 và y = X3 xung quanh trục Ox.
Ốịiải
Phương trình hoành độ giao điểm của hai đồ thị là:
2x2 = X3 x2(2 - x) - 0
Với X 6 [0; 2] thì 2x2 > X3 nên thể tích vật thể tròn xoay là:
V = 71 J [(2x2)2 - (x3)2]dx = 71 J (4x4 - x6)dx 0 0
lõ 7
25671
35
Giãi các phương trình sau trên tập sô' phức:
a) (3 + 2i)z - (4 +-7Ĩ) = 2 - 5i;
z2 - 2z + 13 = 0;
b) (7 - 3i)z + (2 + 3i) = (5 - 4i)z;
z4 - z2 - 6 = 0.
Ốjiảí
a) (3 + 2i)z - (4 + 7i) = 2 - 5i (2 - 5i) + (4 + 7i)
z =
3 + 2i
z -
6 + 2i
3 + 2i
z -
22 6
13 13
(7 - 3i)z + (2 + 3i) = (5 - 4i)z (5 - 4i - 7 + 3i)z = 2 + 3i
z - -
2 + 3i
7 4
2 + i
Phương trình đã cho có A' = 1 - 13 = 12i2 nên z = 1 ± 2 73 i
Đặt t = z2, ta có phương, trình bậc hai t2 - t - 6 = 0 với hai nghiệm là t = -2, t = 3.
Vậy phương trình đã cho có bốn nghiêm là zli2 = ±73 , z3,4 = ±72 i
Trên mặt phăng tọa độ, hãy tìm tập hợp điểm biếu diễn sô' phức z thỏa mãn bất đẳng thức:
a) |z I <2
c) I z - 1 - i I < 1.
b) i z - i I <1
Ốjiải
Giả sử sô' phức có dạng: z = X + yi; X, y e K; i2 = -1
Ta có I z 1 X2 + y2 < 4
Vậy tập hợp điểm biểu diễn số phức z có môđun nhỏ hơn 2 là hình tròn có tâm tại gốc tọa độ, bán kính 2 (không kể biên).
Ta có z - i = X + (y - l)i nên
I z - i I 7x2 + (y -1)2 X2 + (y - l)2 < 1
Vậy tập hợp điểm biểu diễn sô' phức z đã cho là hình tròn có tâm tại điểm 1(0; 1), bán kính 1 (kể cả biên).
Ta có z - 1 - i = (x - 1) + (y - l)i nên
I z - 1 - i| 7(x - l)2 + (y - l)2 (x - l)2 + (y - l)2 < 1
Vậy tâp hợp điểm biểu diễn sô' phức z đã cho là hình tròn có tâm tại điểm 1(1; 1), bán kính 1 (không kể biên).