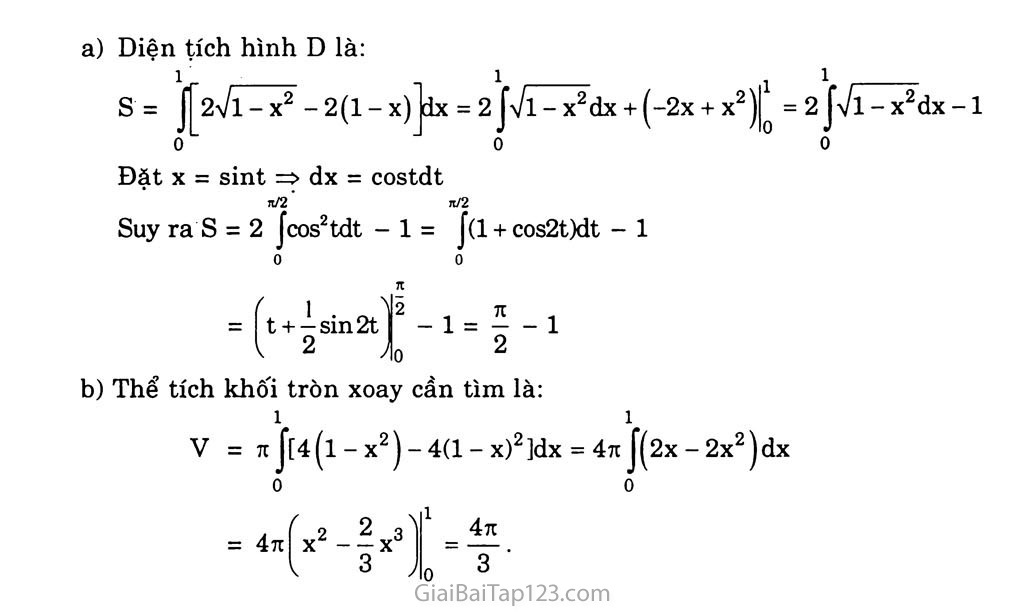Giải toán 12 Ôn tập chương III
ÔN TẬP CHƯƠNG III 3. Tìm nguyên hàm cùa các hàm sô' sau: a) fix) = (x - 1)(1 - 2x)(l - 3x); b) Rx) = sin4xcos22x; c) fix) = —; d) Rx) = (e’ - l)3. 1-x2 tfia’i J(x -1)(1 - 2x)(l - 3x)dx = J(3x - 2x2 - lj(l - 3x)dx = 6x3 - 1 lx2 + 6x -1) dx = X4 - X3 + 3x2 - X + c Jsin4x cos2 2xdx = ì Jsin 4x(l + COS 4x)dx = i Jsin 4xdx + i Jsin 8xdx = - -^cos4x - -^-cos8x + c f_ÈL. = A fi_L.__L.1dx = ì ln Jl-X2 2Ax + 1 X —lj 2 = - ^cos4x - -t-cos8x + c 8 32 + c d) J(ex - l)3 dx = J(e3x - 3e2x + 3ex - l)dx = je3x - je2x + 3ex - X + c . 4. Tính: a) “’í sinxdx ; b) r(x +l)2 (sin X + cosx)2 dx! e) Vĩ J-=4 dx c) 1 + X + Vx g) f~dx; 1 e' + 1 f _ 1 < J (l + x)(2-x) a) Đặt Ốịiảl u = 2 - X Jdu = -dx dv = sinxdx ly = -cosx J(2 - x) sin xdx = (x - 2) COS X - Jcos xdx = (x - 2) COS X - sin X (x + 1) rx +2x + l Ị I I , „2V1„_2„2 , 4 ' - 1 dx = (x2 + 2x2 + X 2)dx = —X2 +-Z J 5 3 = Ậe2x -ex +X + C 3 1 X2 + 2x2 + c J — A./ OX1X AUA — A — ) WO A — [byạìđx = fíù|Ịíidx= Í A-dx; b) Mx; c) fx2e3xdx; d) f Jvi + X J J J 5. Tính: a) + sin 2xdx . ýiải Đặt u = Vl + X =>u2 = l + x=>dx = 2udu Đổi cận: X 0 3 3 ụ 2 2 1 2 2 í r— dx ■ f -2udu = 2 fill2 - J u 1 J\ 1 A±Ẵx = 64 1 f(x3 i 3 ? + x6)dx = (—X3 + J J 1 2 du = 2xdx u = X Đặt A [dv = e3x => dx 1 3x V = -e3 3 2 fx2e3xdx 1 2 = -X ( 2 9 2 ỉ3x -- fxe3xdx J 0 3 0 3 J 0 0 <u3 64 3 1839 14 00 I co Đặt dv = e dx du = dx „ _ 1 3, 2 . 2 -ị [xe3xdx 0 3 J ° 0 2 Suy ra js 0 = je6-ie3*2 =|e6-ị(e6-l) = Je6+ ỉ 3 9 0 3 9' 7 9 9 Vậy fx2e3xdx = ị e6 - I ÍỊeu + ịì = J- (13e6 - 1). J 3 3 1,9 9 27 0 ỵ n K K I d) J7l + sin2xdx = J|sin X + COS x|dx = j\/2 sin(x + j)dx ố 0 0 ( 3 71 4 * sin(x + —)dx - sin(x + —dx J 4 J 4 0 371 V 4 3tĩ = -x/2cos^x + -^J + 72 cos^x + b> J|2X - 2 x|dx; xe3xdx = ^xe' = 272. 6. Tính: a) Jcos2xsin2 xdx ! ú (x + lXx + 2)(x + 3) dx ỉ d) }_4 J X2 - 2x - 3 X e) j(sinx + cosx)2dx ; s> J(x + sinx)2dx • 0 0 2 1 a) Jcos2xsin2 xdx = Jcos2x(l - cos2x)dx 0 2 (’ "7 1 n/f = Jcos2xdx - J(1 - cos4x)dx 0 4 0 1 . " 1, 1 = —sin2x - -4X - —sin4x) = — 4 lo 4 4 1 0 1 b) J|2’-2"*|dx = J(2’-2x)dx + J(2x-2x)dx 1 -1 0 / _ „ \ 0 Z -2"x 2X I f 2X 2"x ln2 ln2 , ln2 ln2 1 ln2 of (x + l)(x + 2)(x + 3) 2 dx= J 1 X3 +6x2 +11X + 6 ■dx _Vfi.ll 6., J X X2 I 2 xji d) f—Ỉ “dx = Ỉ7 7T7 ÍVdx = 7 if—~~ridx Jx2-2x-3 J(x + 1)(x-3) 4Ạx-3 x + lj „ 2 ix2 . . . 6 4— + 6x + lllnlxl 21 2 llln2 = Tln 4 -In 3 n/2 . ' n/2 -£ e) f(sinx + cosx)2dx = J(l + sin2x)dx = (x--^cos2x) 0 (I 2 71 " 7t g) J(x + sinx)2dx = J(x2 + sin2 X + 2xsinx)dx 0 0 71 1 71 V = Jx2dx + - J(1 -cos2x)dx + 2 Jxsinxdx 0 0 0 2=l + 5 0 2 Đặt X ~3 / 1 \ ” * +1 77 - —sin2x + 2 f: <2 2 Jo J X sin xdx du = dx dv = sinxdx V = -cosx 71 7t Suy ra Jx sin xdx = -X COS x|* + Jcos xdx = 71 + sin x|* = 71 0 0 Vậy J(x + sinx)2 dx = . 0 7. Xét hình phẳng D giới hạn bởi y = 2 vl - X2 và y = 2(1 - X) Tính diện tích hình D. Quay hình D xung quanh trục Ox. Tính thế tích khối tròn xoay được tạo thành. y >0 Ta có y = 2 Vl - X2 o Phương trình hoành độ giao điểm của hai đường đã cho là 27Tv = 2(i-x) «7ĨT?=1-x íx < 1 ÍX < 1 (1 - X2 = (1 - x)2 [x2 - X = 0 Diện tích hình D là: 1 1 1 s = J 2V1 -X2-2(l-x)ldx = 2JVl-x2dx + (-2x + X2= 2 Jựl-x2dx-l 0 0 0 Đặt X = sint => dx = costdt n/2 71/2 Suy ra s = 2 Jcos2tdt - 1 = J(1 + cos2t)dt - 1 0 0 = ft + -!-sin2t j2 - 1 = - 1 l 2 X 2 Thể tích khôi tròn xoay cần tìm là: 1 1 V = 71 J[4(l - X2) - 4(1 - x)2]dx = 4n J(2x - 2x2)dx 0 0 = 4x2-j4=4?.