Giải bài tập Toán 9 Bài 1. Một số hệ thức về cạnh và đường cao trong tam giác vuông

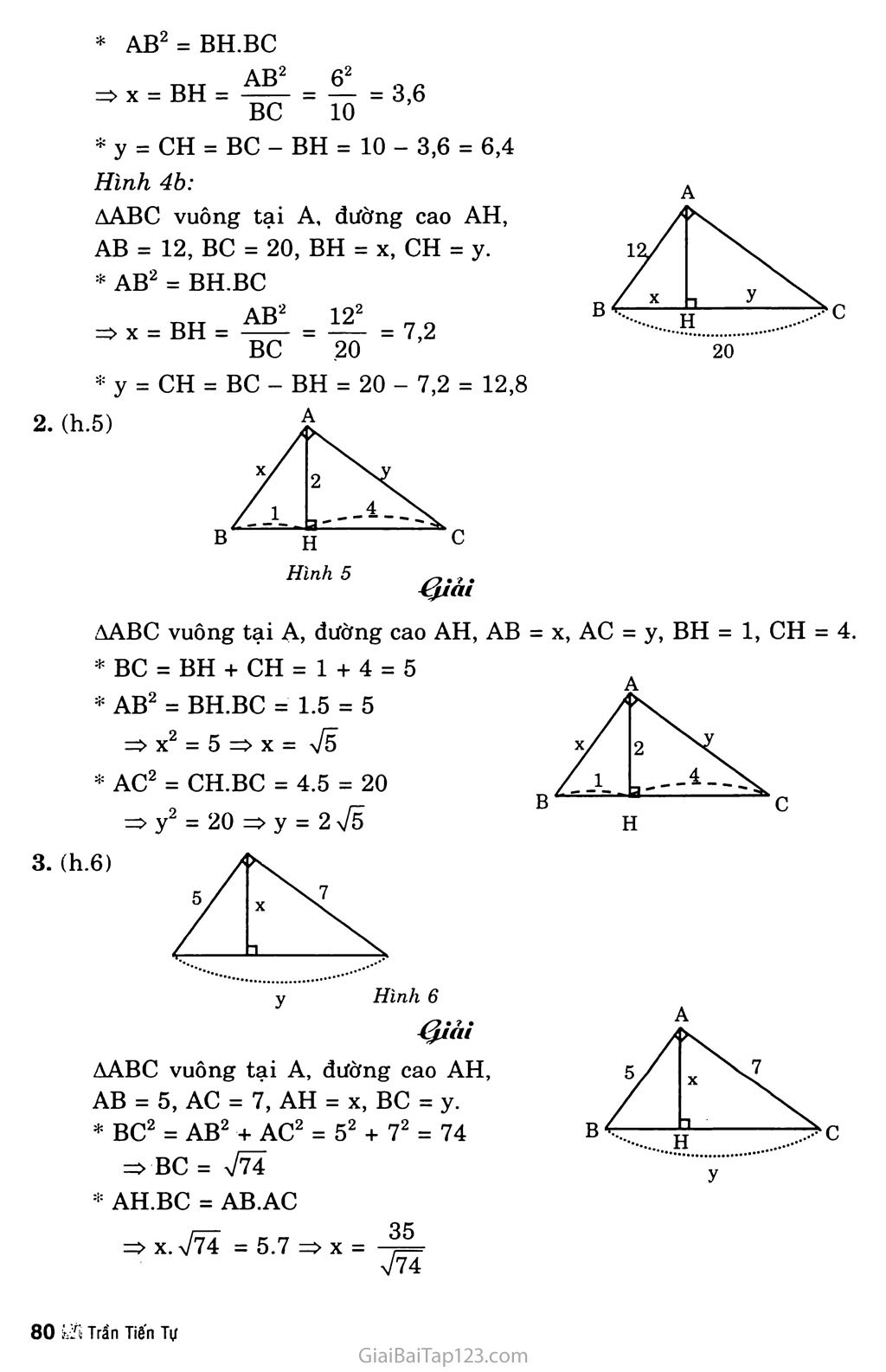
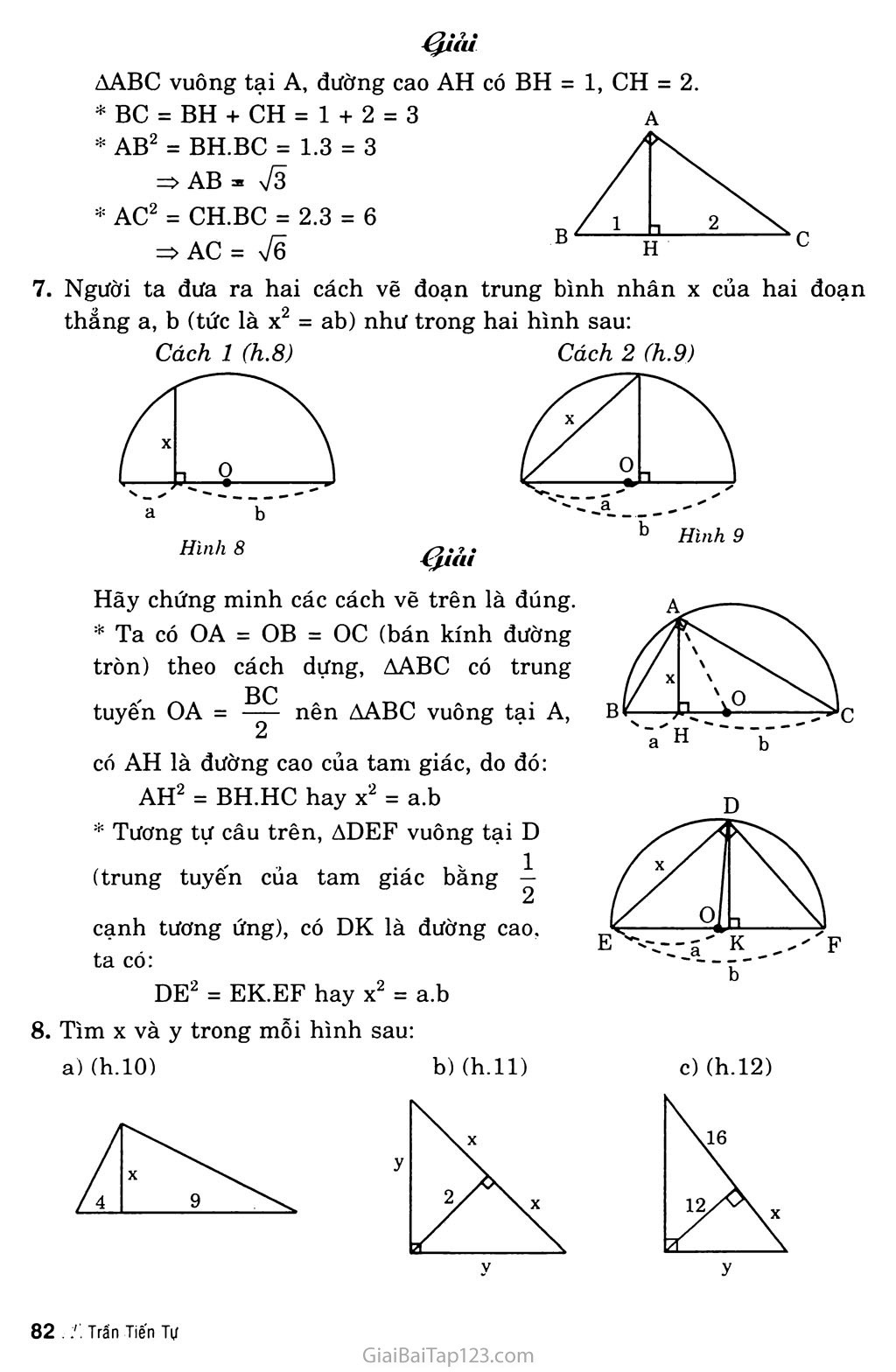
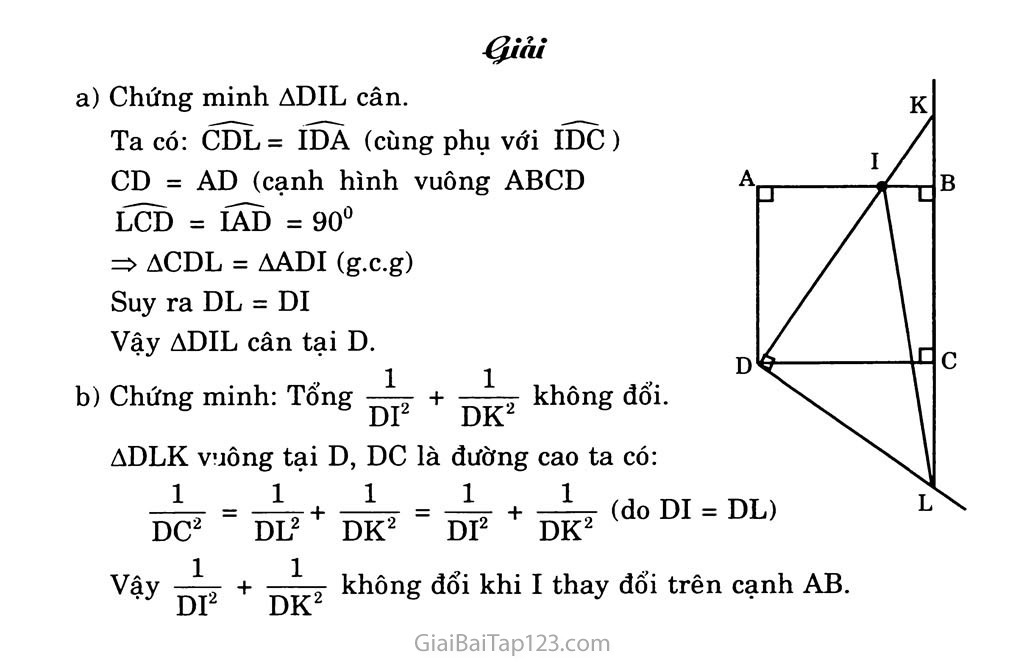
PHẦN HÌNH HỌC
Chương I. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
§1. MỘT SỐ HỆ THỨC VỀ CẠNH
VÀ ĐƯỜNG CAO TRONG TAM GIÁC VUÔNG
A. BÀI TẬP VẬN DỤNG LÍ THUYẾT
?1 Xét hình 1. Chứng minh AAHB ~ ACHA. Từ đó suy ra hệ thức (2).
Hướng dẫn
AAHB ~ ACHA vì có H = 90°; Â = C;
Suy ra:	=> AH2 = CH.BH hay h2 = b’.c’.
CH AH	y
?2 Xét hình 1. Hãy chứng minh hệ thức (3) bằng tam giác đồng dạng.
Hướng dẫn
AAHB ~ ACAB vì có H = Â = 90°; BAH = BCA;
Suy ra: = n*- => AB.CA = AH.CB hay b.c = a.h.
rX-tl vj/x.
B. GIẢI BÀI TẬP
Hãy tính X, y trong mỗi hình sau:
1. (h.4a, b)
a)
Hình 4
^iảì
Hình 4a:
AABC vuông tại A, đường cao AH, AB = 6, AC = 8, BH = X, CH = y.
* BC2 = AB2 + AC2 = 62 + 82 = 100
BC = 10
* AB2 = BH.BC
=> X = BH =
AB2 _ 62
BC “ 10
= 3,6
y = CH = BC - BH = 10 - 3,6 = 6,4 Hình 4b:
AABC vuông tại A, đường cao AH, AB = 12, BC = 20, BH = X, CH = y.
AB2 = BH.BC
=> X = BH = AB?
192 = 7,2
BC 20
2. (h.5)
Hỉnh 5
y = CH = BC - BH = 20 - 7,2 = 12,8
AABC vuông tại A, đường cao AH, AB = X, AC = y, BH = 1, CH = 4.
BC = BH + CH = 1 + 4 = 5
AB2 = BH.BC = 1.5 = 5
=> X2 = 5 => X = Võ
AC2 = CH.BC = 4.5 = 20
AABC vuông tại A, đường cao AH, AB = 5, AC = 7, AH = X, BC = y.
BC2 = AB2 + AC2 = 52 + 72 = 74
=> BC = a/74
AH.BC = AB.AC
=> X. V74 = 5.7 => X = -|r7
V74
4. (h.7)
A
H
_ .„ AB.AC
=> AH = —- 1—
BC
Hình 7
AABC vuông tại A, đường cao AH, AC = y, BH = 1, AH = 2, CH = X.
* AH2 = BH.HC => 22 = 1.x => X = 4
BC = BH + CH = 1 + 4 = 5
AC2 = CH.BC => y2 = 4.5 = 20 => y = J20 = 275
LUYỆN TẬP
Trong tam giác vuông với các cạnh góc vuông có độ dài là 3 và 4, kẻ đường cao ứng với cạnh huyền. Hãy tính đường cao này và độ dài các đoạn thắng mà nó định ra trên cạnh huyền.
AABC vuông tại A, AB = 3, AC = 4. Kẻ đường cao AH ta có:
* BC2 = AB2 + AC2 = 32 + 42 = 25
* AH.BC = AB.AC
-BH=<
BC
* AB2 = BH.BC
CH = BC - BH = 5 - 1,8 = 3,2
Đường cao của một tam giác vuông chia cạnh huyền thành hai đoạn thẳng có độ dài là 1 và 2. Hãy tính các cạnh góc vuông của tam giác này.
AABC vuông tại A, đường cao AH có BH = 1, CH = 2.
BC = BH + CH = 1 + 2 = 3
AB2 = BH.BC = 1.3 = 3
* AC2 = CH.BC = 2.3 = 6
=> AB = Tã
Người ta đưa ra hai cách vẽ đoạn trung bình nhân X của hai đoạn thẳng a, b (tức là X2 = ab) như trong hai hình sau:
Hãy chứng minh các cách vẽ trên là đúng.
Ta có OA = OB = oc (bán kính đường tròn) theo cách dựng, AABC có trung
BC
tuyến OA = —- nên AABC vuông tại A,
2
có AH là đường cao của tam giác, do đó: AH2 = BH.HC hay X2 = a.b
Tương tự câu trên, ADEF vuông tại D (trung tuyến của tam giác bằng —
2 cạnh tương ứng), có DK là đường cao. ta có:
DE2 = EK.EF hay X2 = a.b
8. Tìm X và y trong mỗi hình sau:
a) (h.10)	b) (h.ll)
c)(h.12)
y
^iải
A
AABC vuông tại A, đường cao AH:
AH = X, BH = 4, CH = 9
AH2 = BH.CH
=> X2 = 4.9
X2 = 36
=> X - 6
AABC vuông tại A, đường cao AH.
AH = 2, HB = HC = X, AB = AC = y
* AABC vuông tại A có AB = AC = y nên là tam giác vuông cân
=> ABC = ACB = 45°.
* AAHB vuông tại H, ABH = 45° nên là tam giác vuông cân, do đó X = BH = AH = 2.
AAHC vuông tại H có ACH = 45° nên là tam giác vuông cân.
AB2 = BH.BC => y2 = 2(2 + 2) = 8
y = Vẽ = 2 72
AABC vuông tại A, đường cao AH.
AC = y, CH = X, AH = 12, BH = 16.
Ta có:
Ạ Tj2	1 ọ2
AH2 = BH.CH => X = CH =	= 4=- = 9
BH 16
BC = CH + BH = 9 + 16 = 25
AC2 = CH.BC
=> y2 = 9.25
=> y = 15
Cho hình vuông ABCD. Gọi I là một điểm nằm giữa A và B. Tia DI và tia CB cắt nhau ở K. Kẻ đường thẳng qua D, vuông góc với DI. Đường thẳng này cắt đường thẳng BC tại L. Chứng minh rằng
b) Tổng —+ 1
6 DI2 DK
Tam giác DIL là một tam giác cân.
không đổi khi I thay đổi trên cạnh AB.
^iải
Chứng minh ADIL cân.
Ta có: CDL = IDA (cùng phụ với IDC ) CD = AD (cạnh hình vuông ABCD LCD = ÍẦb = 90°
=> ACDL = AADI (g.c.g)
Suy ra DL = DI
không đổi. DK e
Vậy ADIL cân tại D.
Chứng minh: Tổng +
1
DK2 - DI2
1	—kr (do DI = DL)
DK2
DC2 DL2
1 . 1
Vậy +	-Q-
ỵ DI2 DK
ADLK vuông tại D, DC là đường cao ta có: 1 1
không đổi khi I thay đối trên cạnh AB.