Giải Toán 9: Bài 7. Tứ giác nội tiếp

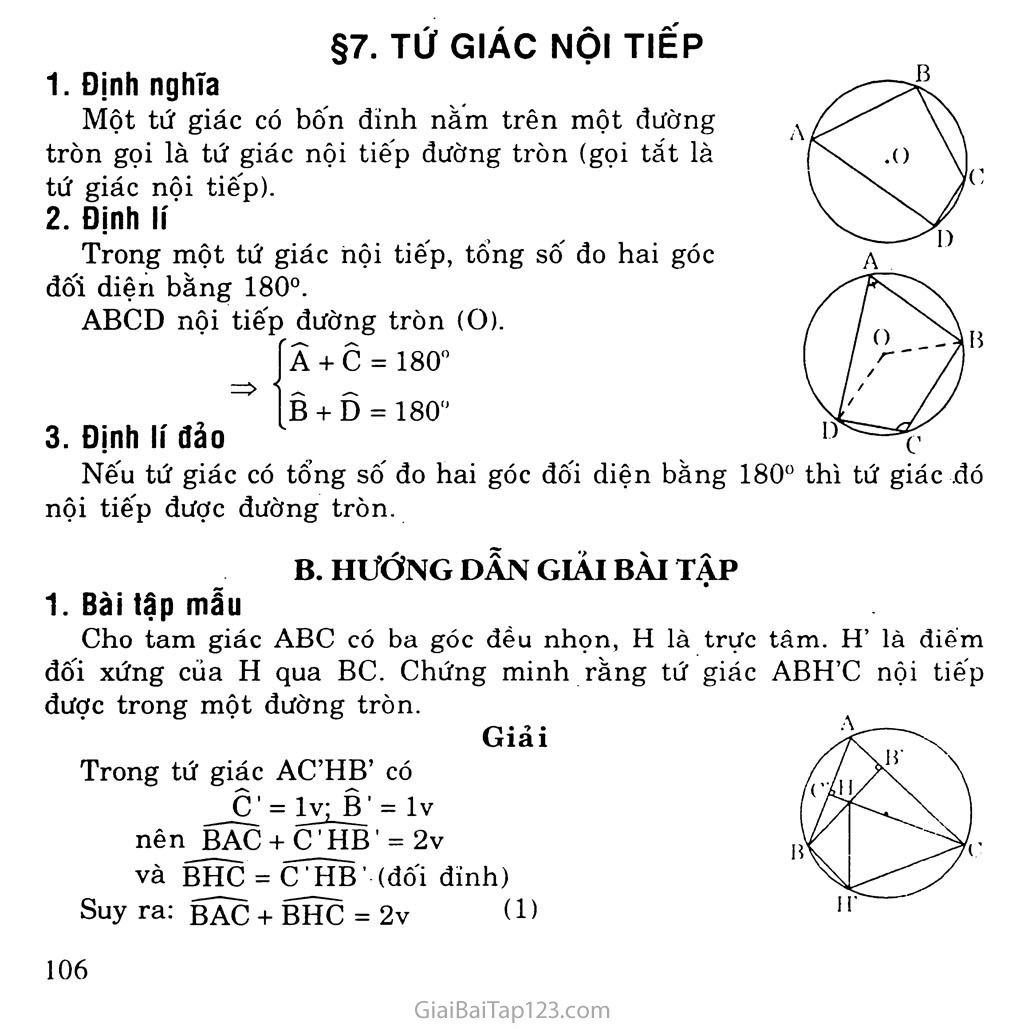
§7. TỨ GIÁC NỘI TIẾP
Định nghĩa
Một tứ giác có bốn đỉnh nằm trên một đường tròn gọi là tứ giác nội tiêp đường tròn (gọi tắt là tứ giác nội tiếp).
Định lí
Trong một tứ giác nội tiếp, tông số đo hai góc đối diện bằng 180°.
ABCD nội tiếp đường tròn (O).
 + C = 180°
B + D . 180°
Định lí đảo	—c
Nếu tứ giác có tổng số đo hai góc đối diện bằng 180° thì tứ giác .đó nội tiếp được đường tròn.
B. HƯỚNG DẨN GIẢI BÀI TẬP
Bài tập mẫu
Cho tam giác ABC có ba góc đều nhọn, H là trực tâm. H’ là điếm đối xứng của H qua BC. Chứng minh rằng tứ giác ABH’C nội tiếp được trong một đường tròn.
Giải
Trong tứ giác AC’HB’ có c' = lv; B ' = lv nên BẠC + C'HB' = 2v và BHC = c'HB• (đối đỉnh)
Suy ra: BÃC + BHC = 2v (!)
c
Vì H’ đối xứng với H qua BC nên suy ra ABHC = ABH’C
nên BHC = BĨ?C	(2)	A
Thay (2) vào (1) ta được
BAC + BITC = 2v
Vậy tứ giác ABH’C nội tiếp được trong một đường tròn.
Bài tập cơ bản
Biết ABCD là tứ giác nội tiếp. Hãy điền vào ô trống trong bảng
sau (nếu có thế):
'Trường hợp Góc
1
2
3
4
5
6
Â
80°
60°
95°
B
70°
40°
65°
C
105°
74°
D
75°
98°
Tứ giác ABCD có ABC + ADC = 180°. Chứng minh rằng các đường trung trực của AC, BD, AB cùng đi qua một điểm.
Cho ABCD là một tứ giác nội tiếp đường tròn tâm M, biết
DAB = 80“. DÂM = 30", BMC = 70° •	 	
Hãy tính số đo các góc MAB, BCM, AMB, DMC, AMD, MCD và BCD ■
Giải
• Trường hợp 1:
Ta có Â + C = 180° => C = 180° - Â = 180° - 80° = 100°
B + D = 180° => D = 180° - B = 180° - 70° =110°
Vậy điền C = 100°, D = 110°.
Trường hợp 2:
Ta có A + C = 180“ => A = 180° - c = 180“ - 105° = 75°
B + D = 18CT => B = 180° - D - 180“ - 75" = 105°
Trườngjiợp^ 3: A + c = 180“ => C = 180~- Â = 180° - 60° = 120° còn lại: B + D = 180". Chẳng hạn chọn B - 70°, D = 110“
Trường hợp 4: D = 180” - B = 180° - 40“ = 140“ __
còn lại A + c = 180" • Chang hạn chọn A - 100", c = 80°
Vậy điền vào ô trống, ta được bảng sau:
^■'MQubng hợp Góc
1
2
3
4
5
6
Â
o
o
00
(75°)
60°
(100°)
(106°)
95°
B
70°
(105°)
(70°)
40°
65°
(82°)
C
(100°)
105°
(120°)
(80°)
74°
(85°)
D
(110°)
75°
(110°)
(140°)
(115°)
98°
Tứ giác ABCD có tống hai góc đối diện bằng 180° nên nội tiếp đường tròn. Gọi tâm đường tròn đó là o, ta có:
OA = OB = oc = OD
Do đó các đường trung trực của AC, BD và AB cùng đi qua o.
Ta có: MAB = DAB-DAM = 80"-30" =50"	(1)
AMBC là tam giác cân (MB = MC) nên BCM-= 180 2 /0 _ 5Ị_0
AMAB là tam giác cân (MA = MB) mà MAB = 50° (theo (D)
Vậy: AMB = 180° - 2 . 50° = 80°	(3)
BAD = Ệ sđBCD (số đo góc nội tiếp bằng nửa số đo của cung bị chắn).
=> sdBCD = 2.BAD = 2.80° =160°
Mà sđBC = BMC = 70° (số đo góc ở tâm bằng số đo cung bị chắn).
Vậy DC - 160° - 70° = 90° (vì điểm c nằm trên cung nhó BD).
Suy ra DMC = 90°	(4)
AMAD là tam giác cân (MA = MD)
Suy ra AMD = 180° -2.30° = 120°	_(5)
AMCD là tam giác vuông cân (MC = MD và DMC = 90")
Suyra MDC = MCD = 45"	.	•
BCD = 100° (theo (2) và (6) và vì CM là tia nằm giữa hai tia CB, CD).
Bài tập tương tự
Cho nửa đường tròn tâm o, đường kính AB. M là một điếm bất kì trên cung AB • Kẻ MD ± AB. Qua một điếm c trên cung MB, kể tiếp tuyên Cx cắt DM tại I. DM cắt AC ở E và cắt BC kéo dài ở F. Chứng minh:
Các tứ giacBCED và ADCF nội tiếp được trong một đường tròn.
MEC = ABC
I là tâm đường tròn ngoại tiếp tam giác FEC.
LUYỆN TẬP
Xem hình 47. Hãy tìm .số đo các góc của tứ giác ABCD.
Trong các hình sau, hình nào nội tiếp được trong một đường tròn: Hình bình hành, hình chữ nhật, hình vuông, hình thang, hình thang vuông, hình thang cân? Vì sao?
Cho tam giác đều ABC. Trên nừa mặt phẳng bờ BC không chứa đỉnh A, lấy điểm D sao cho
DB - DC và DCB = ị ACB .
Chứng minh ABDC là tứ giác nội tiếp.
Cho hình bình hành ABCD. Đường tròn đi qua ba đỉnh A, B, c đường thẳng CD tại p khác c. Chứng' minh AP = AD.
Xem hình 48. Chứng minh QR //.ST.	 	
Hướng dẫn. Xét cặp góc so le trong PST, SRQ.
Giải
56. Ta có: BCE = DCF (hai góc đối đỉnh)
Đặt X = BCE - DCF- Theo tính chất góc ngoài tam giác, ta có:
(1)
(2)
(3)
Xác định tâm của đường tròn đi qua bôn điếm A, B, D, c.
ABC = X + 40°
ADC = X + 20°
Lại có: ABC + ADC = 180°
(hai góc đối diện tứ giác nội tiếp).
Từ (1), (2), (3) suy ra:
180° = 2x + 60° => X = 60°
Từ (1), ta có:
ABC = 60° + 40° = 100°
Từ (2), ta có:
ADC = 60" + 20° = 80“	__
BCD = 180“ - xjhai góc kề bù) => BCD = 120°
BAD = 180" - BCD (hai góc đôi diện của tứ giác nội tiêp)
=> BAD = 180“ - 120" = 60"
Hình bình hành (nói chung) không nội tiếp được
'đường tròn vì tống hai góc đối diện không bằng 180°. Trường hợp riêng của hình bình hành là hình chữ nhật (hay hình vuông) thì nội tiếp đường tròn vì tổng hai góc đối diện là 90° + 90° = 180°.
Hình thang (nói chung), hình thang vuông không nội tiếp được đường tròn.
Hình thang cân ABCD (BC = AD) có hai góc ở mỗi đáy bằng nhau: A = B, c = D; mà A + D = 180° (hai góc trong cùng phía tạo bởi cát tuyến AD với AB // CD), suy ra. A + C = 180" • Vậy hình thang cân luôn có tông hai góc đổì diện bằng 180° nên nội tiếp được đường trộn.
a) Theo giả thiết, DCB = “~ACB = -|.6O" = 30°.
ACD = ACB + BCD (tia^CB nằrrpgiữa hai tia CA, CD).
=> ACD = 60° + 30° = 90°	 (1J 
Do DB = CD nên ABDC cân => DBC = DCB = 3 Từ đó ABD = 60° + 30° = 90°	(2)
Từ (1) và (2) có ACD + ABD = 180° nên tứ giác A nội tiếp được.
b) Vì ABD = 90° nên AD là đường kính của đ tròn ngoại tiếp tứ giác ABDC, do đó tâm đường ngoại tiếp tứ giác ABDC là trung điểm cúa AD.
Do tứ giác ABCP nội tiếp nên ta có:
BAP + BCP = 180"	(1)
Ta lại có: ABC + BCP = 180°	(2)
(hai góc trong cùng phía tạo bởi cát tuyến CB và AB // CD)	
Từ (1) và (2) suy ra: BAP = ABC
Vậy ABCP là hình thang cân, suy ra AP = BC
nhưng BC = AD (hai cạnh đối diện của hình bình hành) (4)
Từ (3) và (4) suy ra AP = AD.
Cách chứng minh khác:
Tứ giác ABCP nội tiếp và lại là hình thang (AB // CD) thì phải là hình thang cân, suy ra AP = BC.
nhưng BC = AD vậy AP = AD.
Kí hiệu như hình vẽ.
Ta có tứ giác ISTM nội tiếp đường tròn nên:
_Si + M = 180"
Mà Ml+Ma=180° (kề bù) nên suy ra Si = Mí)	(1)
Tương tự từ các tứ giác nội tiếp IMPN và INQS ta được	Ma = N.1	(2)
N4 = Ra	'	<3)
Từ (1), (2) và (3) suy ra
Si = Rọ (hai góc ở vị trí so le trong)
Do đó: QR II ST